Уравнение прямой в отрезках. Уравнение прямой в параметрической форме

Уравнение прямой в отрезках имеет вид 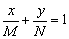, где 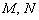– ненулевые константы. Некоторые типы уравнений нельзя представить в таком виде, например, прямую пропорциональность 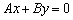(так как свободный член 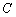равен нулю и единицу в правой части никак не получить).

Это, образно говоря, «технический» тип уравнения. Обыденная задача состоит в том, чтобы общее уравнение прямой 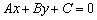представить в виде уравнения прямой в отрезках 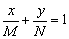. Чем оно удобно? Уравнение прямой в отрезках позволяет быстронайти точки пересечения прямой с координатными осями, что бывает очень важным в некоторых задачах высшей математики.

Найдём точку пересечения прямой с осью 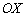. Обнуляем «игрек», и уравнение принимает вид 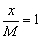. Нужная точка получается автоматически: .

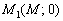Аналогично с осью 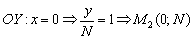– точка, в которой прямая пересекает ось ординат.

Действия, которые я только что подробно разъяснил, выполняются устно.

Пример 11

Дана прямая 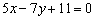. Составить уравнение прямой в отрезках и определить точки пересечения графика с координатными осями.

Решение: Приведём уравнение к виду 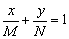. Сначала перенесём свободный член в правую часть:

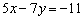
Чтобы получить справа единицу, разделим каждый член уравнения на –11:

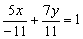
Делаем дроби трёхэтажными:

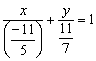
Точки пересечения прямой с координатными осями всплыли на поверхность:

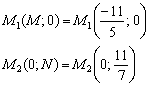
Ответ: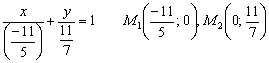

Осталось приложить линеечку и провести прямую.
Но я лучше в очередной раз напрягу Эксель:

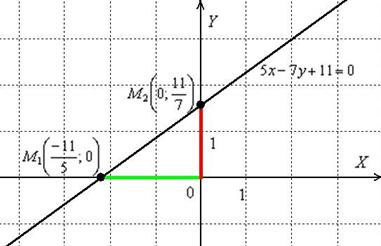
Легко усмотреть, что данная прямая однозначно определяется красным и зелёным отрезками, отсюда и название – «уравнение прямой в отрезках».

Конечно, точки 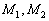не так трудно найти и из уравнения 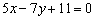, но задача всё равно полезная. Рассмотренный алгоритм потребуется для нахождения точек пересечения плоскости с координатными осями, для приведения уравнения линии второго порядка к каноническому виду и в некоторых других задачах. Поэтому пара прямых для самостоятельного решения:

Пример 12

Составить уравнение прямой в отрезках и определить точки её пересечения с координатными осями.

а)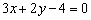

б)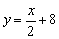

Решения и ответы в конце урока. Не забывайте, что при желании всё можно начертить.

Date: 2015-04-23; view: 1653; Нарушение авторских прав