
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Активные и индуктивные сопротивления обмоток
|
|
Основные положения. Определение активных и индуктивных сопротивлений статора и ротора – параметров схемы замещения асинхронной машины – необходимо для расчета режима х. х., номинальных параметров, рабочих и пусковых характеристик, а также построения круговых диаграмм.
Активные сопротивления рассчитывают для температуры 200С, а при определении потерь их приводят к стандартной рабочей температуре по ГОСТ 183, как указано в § 4-2, путем умножения их на коэффициент тТ.
При расчете индуктивных сопротивлений поле рассеяния условно разбивают на три составляющие: пазовое, дифференциальное и лобовых частей обмоток. Для каждой составляющей определяют магнитную проводимость ( ;
; 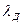 ;
; 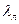 ); суммируют эти проводимости и по ним рассчитывают индуктивное сопротивление.
); суммируют эти проводимости и по ним рассчитывают индуктивное сопротивление.
Проводимость пазового рассеивания зависит от формы и размеров паза. В двухслойных обмотках с укороченным шагом в некоторых пазах располагаются катушки или стержни, принадлежащие разным фазам, вследствии чего потокосцепление такой обмотки уменьшается. Это явление учитывается введением в расчетные формулы коэффициентов 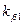 и
и 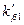 , зависящих от
, зависящих от  1.
1.
Проводимость дифференциального рассеяния обусловлена высшими гармоническими. Высшие гармоники поля статора наводят токи в обмотке ротора; демпфирующую реакцию этих токов учитывают только при короткозамкнутом роторе. Скос пазов уменьшает демпфирующую реакцию токов.
Проводимость рассеяния лобовых частей обмотки зависит от количества пазов на полюс и фазу, длины лобовой части катушки и от укорочения шага обмотки.
При пуске асинхронных двигателей с короткозамкнутым ротором, имеющим глубокие пазы или двойную клетку, в том числе и в виде бутылочного паза, возникает явление вытеснения тока в обмотке ротора, которое приводит к увеличению активного и уменьшению индуктивного сопротивления этой обмотки.
Кроме того, при пуске, а также в режимах работы от s =1 до s max (соответствующем М max) следует учитывать явление насыщения путем потоков рассеяния, которое зависит от величины токов, протекающих в пазах, и уменьшает индуктивные сопротивления статора и ротора. Таким образом, разным режимам работы двигателя – номинальному, пусковому и при М max – соответствуют различные значения r ’2, x 1 и x ’2.
В настоящем разделе приведены формулы для определения активных и индуктивных сопротивлений обмоток при температуре 200С и без учета влияния явлений вытеснения тока в обмотке короткозамкнутого ротора и насыщения путей потоков рассеяния статора и ротора.
Активные и индуктивные сопротивления обмотки статора в относительных единицах (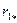 , x 1*) можно определить по разным формулам, но результат должен быть одинаков. Этим проверяется правильность определения r1 и x1. О правильности расчета x ’2 можно примерно судить по отношению x 1 / x’ 2 = 0,7÷1,0.
, x 1*) можно определить по разным формулам, но результат должен быть одинаков. Этим проверяется правильность определения r1 и x1. О правильности расчета x ’2 можно примерно судить по отношению x 1 / x’ 2 = 0,7÷1,0.
Сопротивление обмотки статора. Расчет сопротивления обмотки статора проводят в такой последовательности.
| Активное сопротивление обмотки фазы при 200С (Ом) | 
| (9-178) |
| То же (о. е.) | 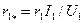
| (9-179) |
Проверка правильности определения 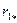 (о. е.) (о. е.)
| 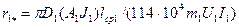
| (9-180) |
Коэффициенты, учитывающие укорочение шага
при  1 = 0,65÷1,0 1 = 0,65÷1,0
| 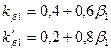
| (9-181) (9-182) |
при  1<0,65 1<0,65
| 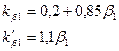
| (9-183) (9-184) |
| Коэффициент проводимости расеяния: для трапецеидального полузакрытого паза (рис. 9-7) | 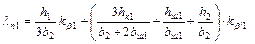
| (9-185) |
| для прямоугольного полуоткрытого паза (рис. 9-9) | 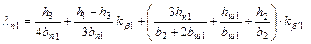
| (9-186) |
| для прямоугольного открытого паза (рис. 9-9) | 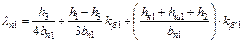
| (9-187) |
| Коэффициент, учитывающий влияние открытия пазов статора на проводимость дифференциального рассеяния | 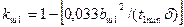
| (9-188) |
| Коэффициент проводимости дифференциального рассеяния | 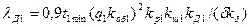
| (9-189) |
| Полюсное деление (мм) | 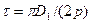
| (9-190) |
| Коэффициент проводимости рассеяния лобовых частей обмотки | 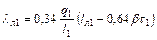
| (9-191) |
| Коэффициент проводимости рассеяния обмотки статора | 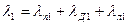
| (9-192) |
| Индуктивное сопротивление обмотки фазы статора (Ом) | 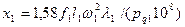
| (9-193) |
| Индуктивное сопротивление обмотки фазы статора (о. е.) | 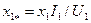
| (9-194) |
| Проверка правильности определения x 1* (о. е.) | 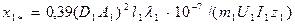
| (9-195) |
Здесь 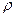 м20=57 См / мкм – удельная электрическая проводимость меди при 200С; h к1, h 2, h 3 – размеры частей обмоток и паза (рис. 9-7 и 9-9), определяемые по табл. 9-21; размер обмотки
м20=57 См / мкм – удельная электрическая проводимость меди при 200С; h к1, h 2, h 3 – размеры частей обмоток и паза (рис. 9-7 и 9-9), определяемые по табл. 9-21; размер обмотки 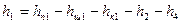 ; k р1 – коэффициент, учитывающий демпфирующую реакцию токов, наведенных в обмотке короткозамкнутого ротора высшими гармониками поля статора (для двигателей с фазным ротором k р1 = 1; для двигателей с короткозамкнутым ротором значения k р1 приведены в табл. 9-22); k д1 – коэффициент дифференциального рассеяния статора, равный отношению суммы ЭДС, наведенных высшими гармониками поля статора, к ЭДС, наведенной первой гармоникой того же поля; k д1 определяют по табл. 9-23.
; k р1 – коэффициент, учитывающий демпфирующую реакцию токов, наведенных в обмотке короткозамкнутого ротора высшими гармониками поля статора (для двигателей с фазным ротором k р1 = 1; для двигателей с короткозамкнутым ротором значения k р1 приведены в табл. 9-22); k д1 – коэффициент дифференциального рассеяния статора, равный отношению суммы ЭДС, наведенных высшими гармониками поля статора, к ЭДС, наведенной первой гармоникой того же поля; k д1 определяют по табл. 9-23.
Таблица 9-21
| Форма паза статора | Высоты, мм | |||
| h | h к1 | h 2 | h 3; h 4 | |
| Полузакрытая | 50 – 132 | 0,7 | 0,6 | |
| 160 – 250 | 1,0 | 0,4 | ||
| 280 – 315 | 3,0 | 0,4 | ||
| Полуоткрытая и открытая | 280 – 355 | 3,0 | 1,9 | 1,0 |
| 400 – 450 | 3,5 | 2,55 | 5,0 |
Таблица 9-22
| q 1 | k р1 при следующих значениях z 2 / p | ||||||

| 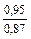
| 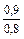
| 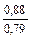
| — | — | — | |

| 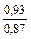
| 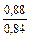
| 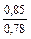
| 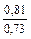
| — | — | |
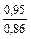
| 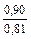
| 
| 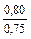
| 
| 
| — | |
| — | 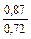
| 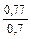
| 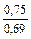
| 
| 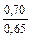
| 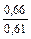
| |
| — | — | — | 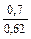
| 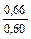
| 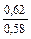
| 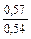
| |
| — | — | — | — | 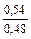
| 
| 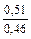
| |
| Примечания: 1. В числителе приведены значения k р1 при скоосе пазов b c = t2, а в знаменателе – при отсутствии скоса пазов. 2. Для значений z 2 / p, отличающихся от приведенных в таблице и для дробных q 1, коэффициент следует определять интерполяцией. |
Таблица 9-23
| q 1 | Коэффициент k д1 | ||
| однослойная обмотка с диаметральным шагом | двухслойная обмотка с укороченным шагом для ротора | ||
| короткозамкнутого | фазного | ||
| 1,5 | — | 0,045 | 0,470 |
| 0,0285 | 0,0235 | 0,0235 | |
| 2,5 | — | 0,0170 | 0,0180 |
| 0,0141 | 0,0111 | 0,0111 | |
| 0,0089 | 0,0062 | 0,0062 | |
| 0,0065 | 0,0043 | 0,0043 | |
| 0,0052 | 0,0030 | 0,0030 | |
| — | 0,0021 | 0,0021 |
Сопротивление обмотки короткозамкнутого ротора с овальными полузакрытыми и закрытыми пазами. Расчет сопротивления обмотки ротора проводят в такой последовательности.
| Активное сопротивление стержня клетки при 200С (Ом) | 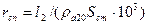
| (9-196) |
| Коэффициент приведения тока кольца к току стержня | при 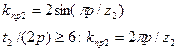
| (9-197) (9-198) |
| Сопротивление короткозамыкающих колец, приведенное к току стержня при 200С (Ом) | 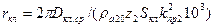
| (9-199) |
| Центральный угол скоса пазов (рад) | 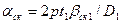
| (9-200) |
| Коэффициент скоса пазов ротора | k ск – по рис. 9-16 | |
| Коэффициент приведения сопротивления обмотки ротора к обмотке статора | 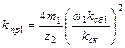
| (9-201) |
| Активное сопротивление обмотки при 200С, приведенное к обмотке статора (Ом) | 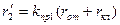
| (9-202) |
| Активное сопротивление обмотки при 200С, приведенное к обмотке статора (о. е.) | 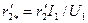
| (9-203) |
| Ток стержня ротора для рабочего режима (А) | 
| (9-204) |
| Коэффициент проводимости рассеяния: для овального полузакрытого паза ротора (рис. 9-10, а) | 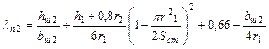
| (9-205) |
| для овального закрытого паза (рис. 9-10, б) | 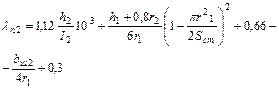
| (9-206) |
| Количество пазов ротора на полюс и фазу | 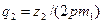
| (9-8 а) |
| Коэффициент дифференциального рассеяния ротора | 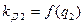 – по рис. 9-17 – по рис. 9-17
| |
| Коэффициент проводимости дифференциального рассеяния | 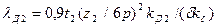
| (9-207) |
| Коэффициент проводимости рассеяния короткозамыкающих колец литой клетки | 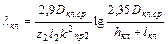
| (9-208) |
| Относительный скос пазов ротора, в долях зубцового деления ротора | 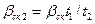
| (9-209) |
| Коэффициент проводимости рассеяния скоса пазов | 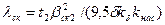
| (9-210) |
| Коэффициент проводимости рассеяния обмотки ротора | 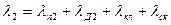
| (9-211) |
| Индуктивное сопротивление обмотки ротора (Ом) | 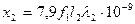
| (9-212) |
| Индуктивное сопротивление обмотки ротора, приведенное к обмотке статора (Ом) | 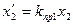
| (9-213) |
| Индуктивное сопротивление обмотки ротора, приведенное к обмотке статора (о. е.) | 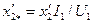
| (9-214) |
| Проверка правильности определения x ’2 | 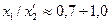
| (9-215) |
Здесь 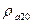 – удельная электрическая проводимость алюминия при 200С [при использовании для заливки беличьей клетки ротора алюминия А5 (обычно применяемый) – удельная электрическая проводимость алюминия при 200С [при использовании для заливки беличьей клетки ротора алюминия А5 (обычно применяемый) 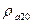 = 27 См / мкм, при использовании алюминиевого сплава АКМ12-4 (для асинхронных двигателей с повышенным скольжением) = 27 См / мкм, при использовании алюминиевого сплава АКМ12-4 (для асинхронных двигателей с повышенным скольжением) 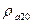 = 15 См / мкм]. = 15 См / мкм].
|
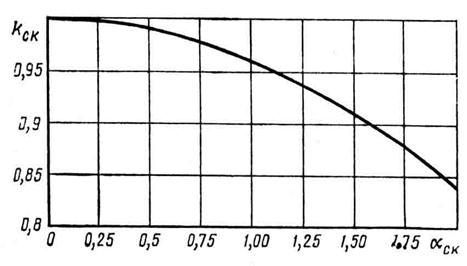
Рис.9-16 Зависимость 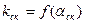
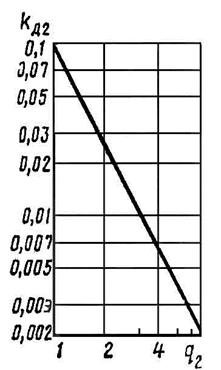
Рис.9-17. Зависимость kД2=f(q2)
для короткозамкнутого рото ра
Сопротивление обмотки короткозамкнутого ротора с бутылочными закрытыми пазами. На рис. 9-18 приведена схема замещения ротора с бутылочными пазами. Обычно такие роторы выполняют без скоса пазов. Высота верхней части бутылочного паза h ≤15 мм; вытеснение тока при пуске двигателя в этой части паза можно не учитывать. Для нижней части паза расчет проводят так же, как для овального паза с заменой индексов (добавление в индексе буквы «н»).
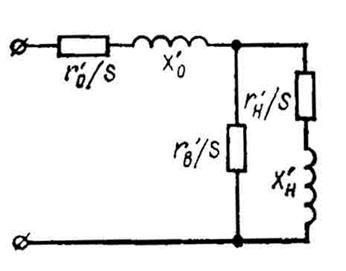
+Рис.9-18. схема замещения ротора с бутылочными пазами
Расчет сопротивления обмотки ротора проводят в такой последовательности.
| Активное сопротивление верхней части стержня при 20 0С (Ом) | 
| (9-216) |
| Сопротивление короткозамыкающих колец, приведенное к току стержня при 20 0С | r кл (Ом) – по (9-199) | |
| Активное сопротивление верхней части стержня, приведенное к статору, при 20 0С (Ом) | 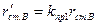
| (9-217) |
| Активное сопротивление нижней части стержня, при 20 0С (Ом) | 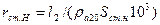
| (9-218) |
| Активное сопротивление нижней части стержня, приведенное к статору, при 20 0С (Ом) | 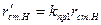
| (9-219) |
| Активное сопротивление короткозамыкающих колец (общей цепи ротора), приведенное к статору, при 20 0С (Ом) | 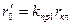
| (9-220) |
| Активное результирующее сопротивление ротора, при 20 0С (Ом) | 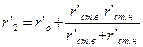
| (9-221) |
| Коэффициент проводимости рассеяния нижней части клетки | 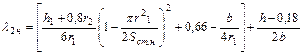
| (9-222) |
| Суммарный ток (А) верхней и нижней частей стержня |  2 – по (9-204) 2 – по (9-204)
| |
| Коэффициент проводимости рассеяния взаимной индукции нижнего и верхнего пазов | 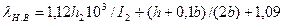
| (9-223) |
| Коэффициент проводимости дифференциального рассеяния | 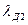 – по (9-207) – по (9-207)
| |
| Коэффициент проводимости рассеяния короткозамыкающих колец | 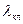 – по (9-208) – по (9-208)
| |
| Коэффициент проводимости рассеяния общей части ротора | 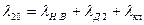
| (9-224) |
| Приведенный коэффициент проводимости рассеяния нижней части клетки | 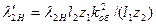
| (9-225) |
| Приведенный коэффициент проводимости рассеяния общей цепи ротора | 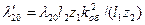
| (9-226) |
| Индуктивное сопротивление нижней части клетки, приведенное к статору (Ом) | 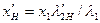
| (9-227) |
| Индуктивное сопротивление общей цепи ротора, приведенное к статору (Ом) | 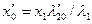
| (9-228) |
| Индуктивное результирующее сопротивление (Ом) | 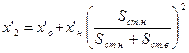
| (9-229) |
| Активное приведенное результирующее сопротивление ротора (о. е.) | 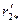 – по (9-203) – по (9-203)
| |
| Индуктивное приведенное результирующее сопротивления обмотки ротора (о. е.) | 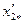 – по (9-214) – по (9-214)
|
Сопротивление обмотки короткозамкнутого ротора с прямоугольными открытыми пазами и сварной клеткой. Расчет сопротивлений обмотки ротора с прямоугольными открытыми пазами и сварной клеткой проводят аналогично расчету для ротора с овальными пазами, но со следующими особенностями. При определении активного сопротивления стержня клетки необходимо в (9-196) добавить слагаемое, учитывающее сопротивление лобовых частей стержня (Ом)
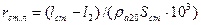 , (9-230)
, (9-230)
а также принять проводимость алюминиевых стержней при 200С равной 30; поэтому в (9-196) в знаменателе следует подставить  = 30.
= 30.
Как правило, двигатели с прямоугольными открытыми пазами ротора и со сварной клеткой выполняются без скоса пазов; поэтому k ск = 0 и 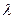 ск = 0. Коэффициент проводимости рассеяния прямоугольного открытого паза
ск = 0. Коэффициент проводимости рассеяния прямоугольного открытого паза
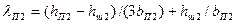 . (9-231)
. (9-231)
Коэффициент проводимости рассеяния короткозамыкающих колец сварной клетки.
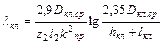 (9-232)
(9-232)
Сопротивление обмотки фазного ротора. Расчет сопротивления обмотки ротора проводят в такой последовательности.
| Активное сопротивление обмотки фазы при 200С (Ом) | 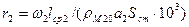
| (9-233) |
| Коэффициент приведения обмотки ротора к обмотке статора | 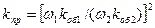
| (9-234) |
| Активное сопротивление обмотки фазы ротора, приведенное к обмотке статора (Ом) | 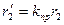
| (9-235) |
| Активное сопротивление обмотки фазы ротора, приведенное к обмотке статора (о. е.) | 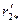 – по (9-203) – по (9-203)
| |
| Коэффициенты, учитывающие укорочение шага | 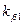 – по (9-181) или (9-183), а – по (9-181) или (9-183), а 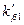 – по (9-182) или (9-184) – по (9-182) или (9-184)
| |
| Коэффициент проводимости рассеяния паза | 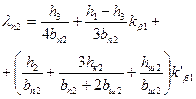
| (9-236) |
| Коэффициент, учитывающий влияние открытия пазов ротора на проводимость дифференциального рассеяния | 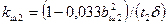
| (9-237) |
| Коэффициент проводимости дифференциального рассеяния | 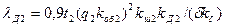
| (9-238) |
| Полюсное деление (мм) | 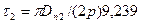
| (9-239) |
| Коэффициент проводимости рассеяния лобовых частей обмотки | 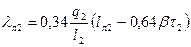
| (9-240) |
| Коэффициент проводимости рассеяния обмотки | 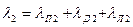
| (9-241) |
| Индуктивное сопротивление обмотки фазы ротора (Ом) | 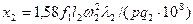
| (9-242) |
| Индуктивное приведенное сопротивление обмотки фазы ротора (Ом) | 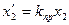
| (9-243) |
| Индуктивное приведенное сопротивление обмотки фазы ротора (о. е.) | 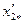 – по (9-214) – по (9-214)
| |
| Проверка правильности определения x ’2 | 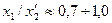
| (9-215) |
| Здесь h 1, h 2, h 3, h к2, h ш2, b п2, b ш2 – размеры частей обмоток и паза, обозначенные на рис. 9-15. Указания по выбору размеров h к2, h ш2, b п2, b ш2, b ст приведены в § 9-6; параметры h 2 = 1,1 мм, h 4 = h 3 = 1,6 мм (при U к ≤ 750 В), h 2 = 1,7 мм, h 4 = h 3 = 2,9 мм (при U к>750 В); размер обмотки h 1 = h п2 – h ш2 – h к2 – h 2 – h 4; k д2 – коэффициент дифференциального рассеяния, определенный по рис. 9-19. |

Рис.9-19. Зависимость KД2=f(q2) для фазного ротора
Сопротивления обмоток преобразованной схемы замещения двигателя (с вынесенным на зажимы намагничивающим контуром). Для расчета различных режимов работы асин
хронного двигателя удобнее пользоваться схемой замещения двигателя с вынесенным на зажимы намагничивающим контуром. При этом сопротивления обмоток двигателя r 1, x 1, r’ 2, x’ 2, определенные для Т-образной схемы замещения, должны быть преобразованы путем умножения на некоторые комплексные коэффициенты [28]. Кроме того, активные сопротивления статора и ротора должны быть умножены на коэффициент т Т (см. § 4-1), т. е. приведены к расчетной рабочей температуре, соответствующей классу нагревостойкости примененных изоляционных материалов и обмоточных проводов.
Введем следующие понятия: коэффициент рассеяния статора
 (9-244)
(9-244)
коэффициент сопротивления статора
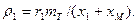 (9-245)
(9-245)
Тогда преобразованные сопротивления обмоток
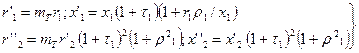 (9-246)
(9-246)
Когда 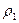 ≤ 0,1(а также случаи встречаются достаточно часто), можно пользоваться упрощенными формулами
≤ 0,1(а также случаи встречаются достаточно часто), можно пользоваться упрощенными формулами
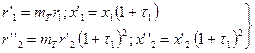 (9-247)
(9-247)
Значение коэффициента 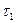 позволяет определить необходимость повторного расчета магнитной цепи; это требуется при коэффициенте насыщения k нас≥ 1,7 и
позволяет определить необходимость повторного расчета магнитной цепи; это требуется при коэффициенте насыщения k нас≥ 1,7 и 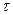 1≥ 0,05. Тогда определяют ЭДС х. х. (В)
1≥ 0,05. Тогда определяют ЭДС х. х. (В)
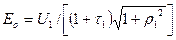 (9-248)
(9-248)
Если Е о из (9-248) отличается от Е = k н U 1 из (9-175) более чем на 3%, то повторяют расчет магнитной цепи по (9-116) – (9-177) при магнтных индукциях 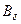 , В з1, В з2, В с1, В с2, измененных пропорционально отношению Е о / Е.
, В з1, В з2, В с1, В с2, измененных пропорционально отношению Е о / Е.
Примеры расчета машин
Date: 2015-05-05; view: 6341; Нарушение авторских прав