
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

V. Засвоєння знань
|
|
План вивчення нового матеріалу
1. Уявлення про основну властивість звичайного дробу; її адаптація на раціональний дріб (із доведенням).
2. Основна властивість дробу і скорочення дробів. Алгоритм скорочення раціонального дробу.
3. Основна властивість дробу і правило знаків.
| Конспект 2 |
| Основна властивість дробу |
1.Якщо 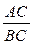 — раціональний дріб, (де В ≠ 0) і С ≠ 0 — раціональний вираз. — раціональний дріб, (де В ≠ 0) і С ≠ 0 — раціональний вираз.
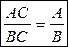 — правило скорочення дробів. — правило скорочення дробів.
|
Приклад.Скоротити дріб 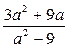 . .
|
| Розв'язання |
1) Розкладемо чисельник і знаменник дробу на множники: 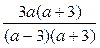 . .
|
2) Поділимо чисельник і знаменник здобутого дробу на спільний множник (а + 3); маємо: 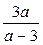 .
Отже: .
Отже: 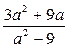 = = 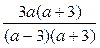 = = 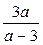 . .
|
2. Якщо 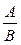 — раціональний дріб (і В ≠ 0), то — раціональний дріб (і В ≠ 0), то
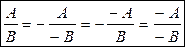 — правило знаків. — правило знаків.
|
Приклад.Скоротити дріб 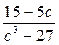 . .
|
1) Розкладемо чисельник і знаменник раціонального дробу на множники:
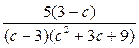 . .
|
2) Помітивши, що (3 – с) і (с – 3) — протилежні вирази, скористаємось правилом знаків: поміняємо, знак перед дробом, і наприклад, знак множника
(3 – с) у чисельнику: 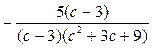 . .
|
3) Скоротивши даний дріб на спільний множник чисельника і знаменника (с–3); маємо: 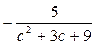 . .
|
Отже, 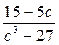 = = 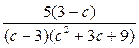 = = 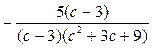 = = 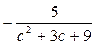 . .
|
3. Якщо 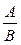 – раціональний дріб (де В ≠ 0) і С ≠ 0 — раціональний вираз, то – раціональний дріб (де В ≠ 0) і С ≠ 0 — раціональний вираз, то
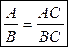 — розширення дробу (зведення дробу до нового знаменника).
Приклад.Звести дріб — розширення дробу (зведення дробу до нового знаменника).
Приклад.Звести дріб 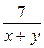 до знаменника х 2 + ху. до знаменника х 2 + ху.
|
| Розв'язання |
1) Розкладемо новий знаменник на множники: х (х + у).
2) Знайдемо додатковий множник; для цього новий знаменник поділимо на знаменник даного дробу.
3) Помножимо чисельник і знаменник даного дробу на х (додатковий множник):  . .
|
@ формулювання і доведення основної властивості раціонального дробу, яка подається як у математичному (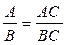 ,
, 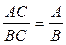 , де А, В, С — деякі многочлени, причому В ≠ 0, С ≠ 0), так і в словесному вигляді.
, де А, В, С — деякі многочлени, причому В ≠ 0, С ≠ 0), так і в словесному вигляді.
Доведення властивості спирається на уявлення про дріб як запис частки від ділення двох виразів та на залежність між компонентами дії ділення.
Після формування в учнів уявлення про «дві сторони» основної властивості раціонального дробу подається назва одного з перетворень, що входять до основної властивості дробу, — скорочення дробів; при цьому наголошується на тому, що під скороченням дробів розуміють ділення чисельника і знаменника раціонального дробу на спільний множник чисельника і знаменника, тому скорочення раціональних дробів передбачає виконання певних дій у певній послідовності для виділення цього спільного множника. Складається алгоритм скорочення раціональна дробів.
Під час розв'язування прикладів на застосування складеного алгоритму скорочення дробів можна запропонувати вправи, що підготують учнів до сприйняття правила знаків для раціональних дробів (або до самостійного складання цього правила в разі високого рівня підготовки учнів до самостійної інтелектуальної діяльності). Після формулювання загального правила розглядаються приклади, під час розв'язування яких необхідно використати правило знаків, та коментуються загальні способи дій у разі застосування цього правила (якщо на опрацювання правила знаків не вистачить часу на уроці № 3, можна розглянути його на уроці № 4 разом із питанням про зведення дробу до нового знаменника).
Date: 2015-04-23; view: 656; Нарушение авторских прав