Явления смачивания и не смачивания. Краевой угол

Если опустить стеклянную палочку в ртуть и затем вынуть ее, то ртути на ней не окажется. Если же эту палочку опустить в воду, то после вытаскивания на ее конце останется капля воды. Этот опыт показывает, что молекулы ртути притягиваются друг к другу сильнее, чем к молекулам стек­ла, а молекулы воды притягива­ются друг к другу слабее, чем к молекулам стекла.

Если молекулы жидкости при­тягиваются друг к другу слабее, чем к молекулам твердого вещества, то жидкость называют сма­чивающей это вещество. Например, вода смачивает чистоестекло и не смачивает парафин. Если молекулы жидкости притя­гиваются друг к другу сильнее, чем к молекулам твердого вещества, то жидкость называют не смачивающей это вещество. Ртуть не смачивает стекло, однако она смачивает чистые медь и цинк.

Расположим горизонтально плоскую пластинку из какого-либо твердого вещества и капнем на нее исследуемую жидкость. Тогда капля расположится либо так, как показано на рис.5(а), либо так, как показано на рис. 5(б).

Рис.5 (а) Рис.5(б)

В первом случае жидкость смачивает твердое вещество, а во втором — нет. Отмеченный на рис.5 угол θ называют краевым углом. Краевой угол образуется плоской поверхностью твердого тела и плоскостью, касательной к свободной поверхности жидкости, где граничат твердое тело, жидкость и газ; внутри крае­вого угла всегда находится жидкость. Для смачивающих жидкостей краевой угол острый, а для не смачивающих — тупой. Чтобы дей­ствие силы тяжести не искажало краевой угол, каплю надо брать как можно меньше.

Поскольку краевой угол θ сохраняется при вертикальном поло­жении твердой поверхности, то смачивающая жидкость у краев сосуда, в который она налита, при­поднимается, а несмачивающая жидкость опускается

Рис 6

При полном смачивании θ = 0, cos θ = 1.

33. Все реальные тела деформируемы. Под действием приложенных сил они меняют свою форму или объем. Такие изменения называются деформациями. В случае твердых тел различают два предельных случая: деформации упругие и деформации пластические.
 Упругими называют деформации, исчезающие после прекращения действия приложенных сил.
Пластическими или остаточными деформациями называют такие деформации, которые сохраняются в теле, по крайней мере частично, и после прекращения действия внешних приложенных сил. На пластических деформациях основана холодная обработка металлов − штамповка, ковка и пр.
 Является ли деформация упругой или пластической зависит не только от материала тела, но и от приложенных сил. Если сила (точнее, сила, отнесенная к единице площади, т. е. напряжение) не превосходит известной величины, называемой пределом упругости, то возникающая деформация будет упругой. Если же она превосходит этот предел, то возникающая деформация будет пластической.
Предел упругости имеет различные значения для разных материалов. Она является не вполне четкой определенной величиной. Разделение тел на упругие и пластические также в какой-то степени условно. Строго говоря, все деформации после прекращения действия внешних сил исчезают не полностью, а поэтому являются пластическими. Однако если остаточные деформации малы, то во многих случаях их можно не принимать во внимание. Как велика должна быть остаточная деформация, чтобы можно было так поступать, зависит от конкретных условий. В некоторых случаях, например, можно пренебречь остаточными деформациями, если они не превосходят 0,1 % от максимальных значений, достигавшихся под действием приложенных сил. В других случаях этот предел должен быть снижен до 0,01 % и т. д.
 Механика описывает упругие свойства тел посредством некоторых эмпирически вводимых упругих постоянных, различных для различных тел и зависящих от их физического состояния (например, от температуры). Более глубоким является физический подход, рассматривающий явление деформаций с атомистической точки зрения. Этим занимается теория твердого тела.
 Она позволяет в принципе не только вывести основные уравнения механики деформируемых тел с атомистической точки зрения, но и установить связь между упругими постоянными вещества и другими его физическими свойствами.
 Тела мы будем считать идеально упругими. Так называются идеализированные тела, которые могут претерпевать только упругие, но не пластические деформации. Такими идеализациями можно пользоваться, когда силы, приложенные к реальным телам, не превосходят предела упругости.
 Для идеально упругих тел существует однозначная зависимость между действующими силами и вызываемыми ими деформациями.
 В случае пластических деформаций такой однозначной связи не существует. Это видно хотя бы из того, что до и после пластической деформации тело имеет различную форму, хотя в обоих случаях оно не подвергается действию внешних сил.
 Малыми называются упругие деформации, подчиняющиеся закону Гука. Это приближенный закон, согласно которому деформации пропорциональны силам, их вызывающим.
 Твердые тела разделяются на изотропные и анизотропные.
 Изотропными называются тела, свойства которых по всем направлениям одинаковы. Анизотропными называются тела, свойства которых в разных направлениях не одинаковы.
 Типичными представителями анизотропных тел являются кристаллы. Приведенные определения отличаются некоторой неопределенностью, поскольку в них явно не указано, о каких физических свойствах идет речь. Дело в том, что тела могут вести себя как изотропные по отношению к одним свойствам и как анизотропные − по отношению к другим. Так, все кристаллы кубической системы ведут себя как изотропные, если речь идет о распространении света в них. Однако они будут анизотропными, если интересоваться их упругими свойствами.
 Металлы обычно имеют поликристаллическую структуру, т. е. состоят из мельчайших беспорядочно ориентированных кристалликов. Каждый из таких кристалликов есть тело анизотропное. Но кусочек металла, содержащий множество их, ведет себя как изотропное тело, если всевозможные ориентации кристалликов представлены с одинаковой вероятностью. В результате пластической деформации хаотичность в ориентации кристалликов может нарушиться. Тогда после пластической деформации металл становится анизотропным. Такое явление наблюдается, например, при вытягивании или кручении проволоки.

Если напряжение, приложенное к металлическому образцу, не слишком велико, то его деформация оказывается упругой – стоит снять напряжение, как его форма восстанавливается. Некоторые металлические конструкции намеренно проектируют так, чтобы они упруго деформировались. Так, от пружин обычно требуется довольно большая упругая деформация. В других случаях упругую деформацию сводят к минимуму. Мосты, балки, механизмы, приборы делают по возможности более жесткими. Упругая деформация металлического образца пропорциональна силе или сумме сил, действующих на него. Это выражается законом Гука, согласно которому напряжение равно упругой деформации, умноженной на постоянный коэффициент пропорциональности, называемый модулем упругости: s = eY, где s – напряжение, e – упругая деформация, а Y – модуль упругости (модуль Юнга

Гука закон, основной закон, выражающий связь между напряжённым состоянием и деформацией упругого тела. Установлен англ. физиком Р. Гуком в 1660 для простейшего случая растяжения или сжатия стержня в форме: абсолютное удлинение (укорочение) Dl цилиндрического стержня прямо пропорционально растягивающей (сжимающей) силе N, т. е. D l = kN, где k = l/ES /l — длина стержня, S — площадь его поперечного сечения, Е — модуль продольной упругости, являющийся механической характеристикой (константой) материала]. Г. з. удобно представлять также в форме s = Е e, где s = N/S — нормальное напряжение в поперечном сечении, e = D l/l — относительное удлинение (укорочение) стержня.

При сдвиге Г. з. записывается так: t = G/g, где t — касательное напряжение, g — сдвиг, G — т. н. модуль сдвига; при сдвиге касательное напряжение прямо пропорционально сдвигу.

Обобщённый Г. з. — для тела произвольной формы — утверждает, что 6 величин, определяющих напряжённое состояние в точке (см. Напряжение механическое), выражаются линейно через 6 величин, определяющих деформацию в окрестности рассматриваемой точки. Коэффициент пропорциональности в этих соотношениях называются модулями упругости. В анизотропных телах, например в кристаллах, модули упругости различны в разных направлениях, поэтому в общем случае упругие свойства твёрдого тела характеризуются с помощью 21 модуля упругости. Для изотропных тел число независимых упругих постоянных сводится к двум (см. Ламе постоянные).

Г. з. не имеет места, когда некоторые напряжения (или деформации) достигают предельных значений, характерных для каждого материала, и тело переходит в упруго-пластическое состояние. Г. з. является основным соотношением, применяемым при расчёте на прочность и деформируемость конструкций и сооружений.

Пластическая деформация — это такая деформация, которая приводит к остаточному изгибу, т.е. тому, который имеет место при удалении внешней нагрузки. Примером такой деформации могут быть свойства алюминиевой проволоки, которую если сильно согнуть и убрать затем внешнее воздействие, то она и остаётся в таком деформированном состоянии по сравнению с исходной формой

Преде́л про́чности — механическое напряжение 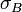, выше которого происходит разрушение материала. Согласно ГОСТу 1497-84 более корректным термином является «Временное сопротивление разрушению», то есть напряжение, соответствующее наибольшему усилию, предшествующему разрыву образца при (статических) механических испытаниях. Термин происходит от того представления, что материал может бесконечно долго выдержать любую статическую нагрузку, если она создаёт напряжения меньшие по величине, чем временное сопротивление. При нагрузке, соответствующей временному сопротивлению (или даже превышающей её — в реальных и квазистатических испытаниях) разрушение материала (разделение образца на несколько частей) произойдёт через какой-то конечный промежуток времени, возможно, что и практически сразу.

Date: 2015-05-04; view: 1210; Нарушение авторских прав