Строение жидкостей

Мы имеем довольно ясное представление о строении газов и твердых кристаллических тел. Газ является собранием молекул, беспорядочно движущихся по всем направлениям независимо друг от друга. В твердом теле все (точнее, почти все) молекулы длительно (иногда тысячелетиями) сохраняют взаимное расположение, совершая лишь небольшие колебания около определенных положений равновесия.

Гораздо более сложным представляется строение жидкостей. Чтобы подойти к этому вопросу, рассмотрим случай, когда в замкнутом сосуде имеется жидкость и ее пар, причем жидкость занимает только часть сосуда (нижнюю); остальное пространство заполнено паром (рис. 396), который, как и всякий газ, заполняет все свободное пространство. Конечно, молекулы и в паре и в жидкости находятся в непрерывном движении и могут вылетать из жидкости и переходить в пар и, обратно, из пара залетать в жидкость. Однако между паром и жидкостью сохраняется (при неизменной температуре) резкая граница, и обмен молекулами не нарушает равновесия между этими двумя состояниями; только это равновесие имеет подвижный (динамический) характер.

Резкая граница между паром и жидкостью разделяет два состояния, или, как говорят, две фазы вещества, из которых парообразная характеризуется гораздо меньшей (в тысячи раз) плотностью, чем жидкая. В жидкой фазе среднее расстояние между молекулами гораздо меньше (в десятки раз), чем в паре, и в соответствии с этим межмолекулярные силы сцепления в жидкости гораздо больше, чем в паре.

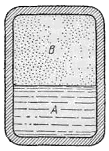
Рис. 396. Объем сосуда делится на две части: в одной из них жидкость A, в другой— пар В
Этим и объясняется различие в характере движения молекул в паре и в жидкости.

В паре, подобно газу, можно почти не учитывать сил сцепления и рассматривать движение как свободный полет молекул и соударение их друг с другом и с окружающими телами (стенками и жидкостью, покрывающей дно сосуда). В жидкости молекулы, как и в твердом теле, сильно взаимодействуют, удерживая друг друга. Однако, в то время как в твердом теле каждая молекула сохраняет неограниченно долго определенное положение равновесия внутри тела и движение ее сводится к колебанию около этого равновесного положения, характер движения в жидкости иной. Молекулы жидкости движутся гораздо свободнее, чем молекулы твердого тела, хотя и не так свободно, как молекулы газа. Каждая молекула в жидкости в течение некоторого времени движется то туда, то сюда, не удаляясь, однако, от своих соседей. Это движение напоминает колебание молекулы твердого тела около положения равновесия. Однако время от времени молекула жидкости вырывается из своего окружения и переходит в другое место, попадая в новое окружение, где опять в течение некоторого времени совершает движение, подобное колебанию.

Таким образом, движение молекул жидкости представляет собой нечто вроде смеси движений в твердом теле и в газе: «колебательное» движение на одном месте сменяется «свободным» переходом из одного места в другое. В соответствии с этим строение жидкости представляет что-то среднее между строением твердого тела и строением газа. Чем выше температура, т. е. чем больше кинетическая энергия молекул жидкости, тем большую роль играет «свободное» движение: тем короче промежутки «колебательного» состояния молекулы и чаще «свободные» переходы, т. е. тем больше жидкость уподобляется газу. При достаточно высокой температуре, характерной для каждой жидкости (так называемой критической температуре, §303), свойства жидкости не отличаются от свойств сильно сжатого газа.

Следует отметить, что мы имеем гораздо менее отчетливые представления о строении жидкостей, чем о строении газов и кристаллических тел, что объясняется гораздо большей сложностью явлений, характеризующих жидкость.

Вязкость -свойство жидкости оказывать сопротивление относительному движению (сдвигу) частиц жидкости. Это свойство обусловлено возникновением в движущейся жидкости сил внутреннего трения, ибо они проявляются только при ее движении благодаря наличию сил сцепления между ее молекулами. Характеристиками вязкости являются: динамический коэффициент вязкости μ и кинематический коэффициент вязкости ν.

Единицей динамического коэффициента вязкости в системе СГС является пуаз (П): 1 П=1 дина·с/см²=1 г/(см·с). Сотая доля пуаза носит название сантипуаз (сП): 1 сП=0,01П. В системе МКГСС единицей динамического коэффициента вязкости является кгс·с/м²; в системе СИ - Па·с. Связь между единицами следующая: 1 П=0,010193 кгс·с/м²=0,1 Па·с; 1 кгс·с/м²=98,1 П=9,81 Па·с.

Кинематический коэффициент вязкости

ν=μ/ρ,

Единицей кинематического коэффициента вязкости в системе СГС является стокc (Ст), или 1 см²/с, а также сантистокс (сСт): 1 сСт=0,01 Ст. В системах МКГСС и СИ единицей кинематического коэффициента вязкости является м²/с: 1 м²/с=10⁴Ст.

Вязкость жидкости с повышением температуры уменьшается. Влияние температуры на динамический коэффициент вязкости жидкостей оценивается формулой μ = μ₀·e^­a(t-t₀⁾, где μ = μ₀ - значения динамического коэффициента вязкости соответственно при температуре t и t₀ градусов; а - показатель степени, зависящий от рода жидкости; для масел, например, значения его изменяются в пределах 0,025—0,035.

Для смазочных масел и жидкостей, применяемых в машинах и гидросистемах, предложена формула, связывающая кинематический коэффициент вязкости и температуру:

ν_t=ν50·(50/t₀)ⁿ,

где ν_t - кинематический коэффициент вязкости при температуре t⁰;
ν50 - кинематический коэффициент вязкости при температуре 50 ⁰С;
t - температура, при которой требуется определить вязкость, ⁰С;
n - показатель степени, изменяющийся в пределах от 1,3 до 3,5 и более в зависимости от значения ν50.

С достаточной точностью n может определяться выражением n =lg ν50 +2,7. Значения n в зависимости от исходной вязкости ν при 50 ⁰С приведены далее в таблице

Значения динамического и кинематического коэффициентов вязкости некоторых жидкостей приведены далее в таблице

Значение коэффициентов кинематической и динамической вязкости пресной воды

КОЭФФИЦИЕНТ СЖИМАЕМОСТИ ЖИДКОСТИ,

(β_ж) в условиях изотермического процесса 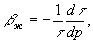где τ объем жидкости, соответствующей давлению Р. Величина β_ж существенно положительная; знак минус в формуле показывает, что объем жидкости увеличивается с уменьшением давления. Так как сжимаемость жидкостей весьма мала, то формулу можно представить приближенно в следующем виде: 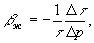где Δ р = р₀ — р₁; р₀ — начальное давление; p_{i —} конечное давление; τ — объем жидкости при р₀; Δ τ — θзменение объема при изменении давления на Δр. Т. о., β_ж равен относительному изменению ее объема при изменении давления на 1 атм (Щелкачев, 1948).

Сжимаемость - свойство жидкости изменять свой объем под действием давления. Сжимаемость жидкостей характеризуется коэффициентом объемного сжатия β_р, который выражает относительное изменение объема жидкости V₀, отнесенное к единице давления p и определяется по формуле

β_р =(- dV/V₀)·(1/ dp ),

Знак минус в формуле обусловлен тем, что положительному прира­щению давления соответствует отрицательное приращение (уменьшение) объема. Единицы измерения β_р в системе МКГСС — м²/кгс, в системе СИ - 1/Па.Часто β_р выражается в см²/кгс.

Если принять, что приращение давления dp = p - р₀, а изменение объема dV=V-V₀, то

V= V₀·(1- β_р· dp ),

ρ = ρ₀ /(1- β_р· dp),

где V и V₀ - объемы, а ρ и ρ₀ - плотности соответственно при давлениях p и р₀.

Величина, обратная коэффициенту объемного сжатия, называется объемным модулем упругости жидкости: Е_ж =1/β_р. Единицы измерения Е_ж те же, что и давления: в системе МКГСС - кгс/м², в системе СИ - Н/м² или Па (паскаль), часто применяется также кгс/см². Значения Е_ж жидкостей зависят от температуры t и давления р.

Различают адиабатический и изотермический модули упругости. Первый несколько больше второго и проявляется при быстротечных процессах сжатия жидкости, например при гидравлическом ударе в трубах.

Изотермический модуля упругости воды в МПа.

При изменении давления и температуры в небольших пределах значение Е_ж можно считать величиной постоянной. Средние значения изотермического модуля упругости некоторых жидкостей приведены далее в таблице.

Динамическая (абсолютная) вязкость µ – сила, действующая на единичную площадь плоской поверхности, которая перемещается с единичной скоростью относительно другой плоской поверхности, находящейся от первой на единичном расстоянии.

В системе СИ динамическая вязкость выражается в Па×с (паскаль-секунда), внесистемная единица П (пуаз).

Соотношение величин динамической вязкости в различных единицах измерения:

1 П = 1 дин×с/см² = 0,010193 кгс×с/м² = 0,1 Па×с
(1 дин = 10⁻⁵ Н = 1,02×10⁻⁶ кгс)
1 сП (сантипуаз) = 1,010193×10⁻⁴ кгс×с/м² = 0,01 П = 10⁻³ Па×с
1 кгс×с/м² = 98,0665 П = 9806,65 сП = 9,80665 Па×с

Кинематическая вязкость ν – отношение динамической вязкости µ к плотности жидкости ρ.

ν= µ / ρ,

где:
ν, м²/с – кинематическая вязкость;
μ, Па×с – динамическая вязкость;
ρ, кг/м³ – плотность жидкости.

В системе СИ кинематическая вязкость выражается в м²/с (квадратный метр на секунду), внесистемная единица Ст (стокс).

Соотношение величин кинематической вязкости в различных единицах измерения:
1 Ст = 10⁻⁴ м²/с = 1 см²/с
1 м²/с = 10⁴ Ст = 10⁶ сСт (сантистокс)

28-31.

Всякий объём жидкости или газа способен как угодно изменять свою форму под действием сколь угодно малых сил. Это общее свойство жидкостей и газов являемся вместе с тем и их общим от­личием от твёрдых тел. Но для изменения самого объёма жид­кости или газа, так же как и в случае твёрдых тел, необходимы ко­нечные внешние силы. Это значит, что при изменении объёма жидкости или газа в нём возникают силы, в конце концов уравно­вешивающие действие внешних сил.

Правда, под действием малых сил изменение формы жидкости или газа может происходить очень медленно; но оно всегда будет проис­ходить до тех пор, пока действуют внешние силы. Любое движение твёрдого тела в жидкости или газе может служить этому подтвер­ждением. Движение тела в жидкости или газе связано с изменением взаимного расположения отдельных частей жидкости или газа. Ме­жду тем это движение возникает под действием каких угодно малых сил.

Жидкости и газы ведут себя как упругие тела только- в от­ношении изменения объёма. Из двух элементарных деформаций — сжатия (растяжения) и сдвига—только первая связана с изменением объёма. Поэтому только в отношении деформаций сжатия и растяже­ния жидкости и газы ведут себя, как упругие тела. Однако и в от­ношении этой деформации есть существенное различие в поведении жидкостей и газов, с одной стороны, и твёрдых тел, — с другой.

Твёрдое тело можно растянуть илн сжать в каком-либо одном направлении. Его можно также сжать во всех направ­лениях, т. е. подвергать всестороннему сжатию или растяжению. В жидкостях же и газах практически приходится иметь дело толь­ко со всесторонним сжатием. Правда, в специальных условиях жидкость может быть подвергнута растяжению; при этой деформа­ции в ней также возникают силы, подобные упругим силам в твёрдом теле. Но в задачах механики эти специальные условия обычно не возникают, и поэтому практически приходится иметь дело только с всесторонним сжатием в жидкости. Что же касается газов, то в них принципиально имеют место только деформации сжатия. Какой бы объём ни занимала данная масса газа, газ всегда оказы­вается сжатым, так как в отсутствие внешних сил объём газа будет увеличиваться беспредельно. Между тем жидкость н отсутствие внеш­них сил занимает определённый объём.

Однако, мы сейчас не рассматриваем различия между жидкостя­ми и газами (это будет сделано позже), а лишь отмечаем их общие черты, отличающие их от твёрдых тел. Общая черта жидкостей и газов состоит в том, что только в отношении деформации всесто­роннего сжатия они ведут себя, как упругие тела. При сжатии жид­кости или газа в них, как и в твёрдом теле, возникают упругие силы, определяемые величиной деформации, т. е. степенью сжатия жидкости или газа. Если бы мы все деформации жидкости относили к нормальному её состоянию, то мы всегда встречались бы с дефор­мациями одного знака (сжатием). Как сказано, для газа такое нор­мальное, несжатое состояние вообще не - имеет смысла вводить. Рассматривая же определённую степень сжатия газа как нормальное состояние, мы встретимся и с увеличением, и с уменьшением степе­ни его сжатия, т. е. с деформациями различных знаков. 'Го'чно так же и для жидкости часто удобно определённую степень сжатия рассма­тривать как «нормальное» состояние и вводить деформации различных знаков. Формально всё будет обстоять так же, как с упругими те­лами,-— можно говорить о сжатии и о «растяжении» жидкости или газа, хотя фактически речь будет итти лишь о разной степени сжатия.

Изменениям формы, не связанным с изменением объёма, соответ­ствует элементарная деформация сдвига. При быстрых деформациях сдвига а жидкости и газе могут возникать заметные силы; однако, эти силы зависят не от величины деформации, а от скорости изме­нения деформации. И если скорость деформаций стремится к нулю,, т;о и силы стремятся к нулю. Поэтому эти силы следует рассматри- аать не как упругие силы, а как силы трения. Эти силы внутрен­него трения называют силами вязкости. С силами вязкости прихо­дится считаться только при рассмотрении достаточно быстрых движений, когда сдвиги в жидкости или газе изменяются с доста­точно большой скоростью. Какая скорость окажется «достаточно- большой» в этом смысле, зависит от свойств жидкости или газа и конкретных условий задачи. Но во всяком случае, для всех кон­кретных условий можно указать столь медленные движения, при ко­торых с силами, возникающими в жидкости и газе при сдвигах, можно не считаться. Разумеется, с этими силами можно не счи­таться при рассмотрении задач о равновесии жидкостей и газов.

Общая черта жидкостей и газов — наличие лишь одного типа упругой деформации всестороннего сжатия — позволяет целый ряд вопросов механики жидкостей и газов рассматривать с общей точки зре­ния. Но между жидкостями и газами есть и ряд существенных различий, которые приводят к различной постановке некоторых вопросов меха­ники в отношении жидкостей и газов. Например, существенное раз­личие жидкостей и газов состоит в том, что упругие свойства газов в гораздо большей степени, чем жидкостей, зависят от температуры. Однако, мы будем полагать, что свойства тел нам заданы и всё вре­мя остаются неизменными, в частности, что все рассматриваемые явления протекают при неизменной температуре. Там, где необходимо учесть изменения температуры газа, будут делаться специальные оговорки.

Жидкость и.газ, так же как и твёрдые тела, мы будем разби­вать на отдельные малые элементы. Эти элементы должны быть столь' малы, чтобы можно было считать все отдельные их атомы движущимися одинаково. Здесь опять речь идёт о регулярном, а не о хаотическом движении атомов. Того обстоятельства, что отдельные атомы вследствие хаотического движения выходят за пределы дан­ного элемента, и их место занимают другие, в макроскопической ме­ханике жидкостей и газов можно не учитывать.

К отдельным малым элементам (которые должны, однако, содер­жать ещё много атомов) мы будем применять общие законы механи­ки. Всякий объём жидкости или газа мы будем рассматривать как систему тйких элементов. Но эти отдельные элементы могут изме­нять взаимное расположение. Поэтому к данному объёму жидкости или газа мы не можем, вообще говоря, применять представлений механики твёрдого тела, так как в твёрдом теле взаимное располо­жение отдельных элементов мы считали неизменным. Для объёма жидкости или газа в общем случае справедливы только положения механики системы точек, не связанных жёстко между собой. Но в том случае, когда речь идёт о покоящейся жидкости или газе или о таких движениях, при которых взаимное расположение отдельных элементов рассматриваемого объёма ие изменяется, мы можем итти дальше и применять к этому объёму положения динамики твёрдого тела. В частности, в таких случаях можно говорить о центре тяже­сти объёма, как о некоторой фиксированной точке, о моменте сил, действующих на объём, перемещать точки приложения сил вдоль направления сил, применять условия равновесия твёрдого тела и т. д. Этог приём получил название принципа отвердения. Мы представ­ляем себе рассматриваемый объём отвердевшим и применяем к нему законы механики твёрдого тела. Ясно, что этот приём допустим только в том случае, если мы заранее уверены, что отдельные эле­менты объёма не изменяют своего взаимного расположения. В частно­сти, принцип отвердения всегда можно применять к покоящимся жид­костям и газам.

1. Кинематическое описание движения жидкости.

При кинематическом описании движения жидкости удобнее всего рассматривать движение жидкости в данный момент времени в данной точке в целом, а не конкретно какой либо молекулы.

Основной характеристикой кинематического движения является скорость, которая характеризуется величиной и направлением в данный момент времени.

Для того чтобы описать движение жидкости рассматривают множество частиц жидкости, которые в различные моменты времени проходят через одну и ту же точку пространства. Если таких точек взять много и при этом зафиксировать время, то, в пространстве получится мгновенная картина распределения скоростей жидкости – поле скоростей. В каждой точке пространства будет указан вектор скорости той частицы жидкости, которая проходит через эту точку в рассматриваемый момент времени. Для графического представления поля скоростей используют линии тока - л инии, в каждой точке которых касательная совпадает по направлению со скоростью частиц жидкости в данный момент времени. Часть жидкости, ограниченную линиями тока называют трубкой тока.

Если поле скоростей, а следовательно, и соответствующие ему линии тока не меняются с течением времени, то движение жидкости называется стационарным или установившимся. Если же они меняются во времени, то движение называется нестационарным или неустановившимся. При стационарном движении скорость от времени не зависит, а зависит только от координат: В этом случае линии тока совпадают с траекториями движения отдельных частиц жидкости.

2. Уравнение движения и равновесия жидкостей.(ни в лекциях ни в учебнике этого нет.завтра спрошу на консультации, что конкретно он имел вииду и исправлю)

Рассмотрим движение идеальной жидкости. Выделим внутри неё некоторый объём V. Согласно второму закону Ньютона, ускорение центра масс этого объёма пропорционально полной силе, действующей на него. В случае идеальной жидкости эта сила сводится к давлению окружающей объём жидкости и, возможно, воздействию внешних силовых полей. Предположим, что это поле представляет собой силы инерции или гравитации, так что эта сила пропорциональна напряжённости поля и массе элемента объёма. Тогда

,

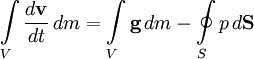где S — поверхность выделенного объёма, g — напряжённость поля. Переходя, согласно формуле Гаусса — Остроградского, от поверхностного интеграла к объёмному и учитывая, что 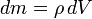, где ρ — плотность жидкости в данной точке, получим:

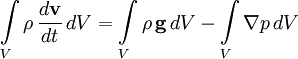
В силу произвольности объёма V подынтегральные функции должны быть равны в любой точке:

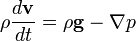
Выражая полную производную через конвективную производную и частную производную:

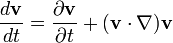
получаем уравнение Эйлера для движения идеальной жидкости в поле тяжести:

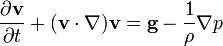
где 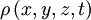— плотность жидкости,
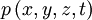— давление в жидкости,
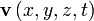— вектор скорости жидкости,
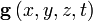— вектор напряжённости силового поля,
— оператор набла для трёхмерного пространства.

3. Идеальная жидкость. Реальная жидкость обладает рядом свойств, таких как, например, вязкость – способность оказывать сопротивление перемещению одних частиц относительно других.Но прирассмотрении движения жидкости принято пользоваться понятием идеальной жидкости, то есть жидкости в которой отсутствует вязкость. Не смотря на то, что Идеальная жидкость — это идеализированная модель жидкости, она даёт достаточно хорошее описание реальных течений жидкостей. Математическое описание течений идеальных жидкостей позволяет найти теоретическое решение ряда задач о движении жидкостей.

НЬЮТОНОВСКАЯ ЖИДКОСТЬ - вязкая жидкость, подчиняющаяся при своём течении закону вязкого трения Ньютона. Для прямолинейного ламинарного течения этот закон устанавливает наличие линейной зависимости между касат. напряжением 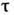в плоскостях соприкосновения слоев жидкости и производной от скорости течения v по направлению нормали п к этим плоскостям, т. 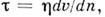е. где 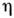- динамич. коэф. вязкости. В общем случае пространств. течения для Н. ж. имеет место линейная зависимость между тензорами напряжений 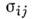и скоростей деформаций Свойствами Н. ж. обладают большинство жидкостей (вода, смазочное масло и др.) и все газы. Течение Н. ж. изучается в гидроаэромеханике (см. Ньютона закон трения ). Жидкости, для к-рых указанные выше зависимости не являются линейными, наз. ненъютоновскими жидкостями. К ним относится ряд суспензий и растворов полимеров. Такие течения изучаетреология.

Гидроста́тика — раздел физики сплошных сред, изучающий равновесие жидкостей, в частности, в поле тяжести.

Прежде всего, полезно сравнить гидростатику с теорией упругости, изучающей равновесие твёрдых тел. В отличие от твёрдого тела, жидкость не «держит» сдвиговые напряжения. Именно поэтому в жидкости не может существовать анизотропии напряжений, а значит вместо многокомпонентного тензора, напряжения в жидкости описываются единственной величиной — давлением. Отсюда вытекает закон Паскаля: давление, оказываемое на жидкость, передаётся жидкостью одинаково во всех направлениях.

Основной закон гидростатики для толщи жидкости — зависимость давления от глубины, который для несжимаемой жидкости в однородном поле тяжести имеет вид P = ρ gh. Из этого закона следует равенство уровней в сообщающихся сосудах, закон Архимеда: на тело, погружённое в жидкость, действует выталкивающая сила F = ρ gV, где ρ — плотность жидкости, а V — объём тела, погруженного в жидкость.

Наглядно представить себе закон Архимеда можно следующим образом. Замена тела помещенного в жидкость на саму эту жидкость ничего не изменит для окружающей тело жидкости. При этом жидкость-заменитель будет невесомой, поскольку она идентична остальной жидкости и иной вес означал бы движение вверх или вниз и возможность получения энергии из ничего. А поскольку жидкость-заменитель "на воздухе" весила бы как раз столько, сколько положено по закону Архимеда, ρ gV, то именно этот вес тело, погружённое в жидкость, теряет.

Форма свободной поверхности жидкости определяется комбинацией внешних сил (прежде всего, сил тяготения) и сил поверхностного натяжения. Для больших масс жидкости преобладают силы тяготения и свободная поверхность принимает форму эквипотенциальной поверхности, а при размерах порядка или меньше сантиметра (для пресной воды) определяющими являются капиллярные силы.

Рассмотрим идеальную жидкость. Идеальная жидкость – жидкость, плотность которой не зависит от давления и постоянна в любой пространственной области, а вязкость (внутреннее трение) отсутствует. При движении идеальной жидкости не происходит превращения механической энергии в тепловую, то есть механическая энергия жидкости сохраняется.

Рассмотрим стационарное течение идеальной жидкости в каком-либо потенциальном силовом поле, например в поле силы тяжести. Применим к этому течению закон сохранения энергии. Выделим в жидкости бесконечно узкую трубку тока и рассмотрим часть жидкости, занимающую объем MNDC. Пусть эта часть переместилась в бесконечно близкое положение 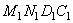(рис. 6.2). При малом перемещении можно пренебречь различием площадей сечений MN и 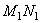, CD и .

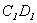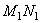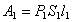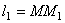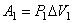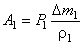Вычислим работу А, совершаемую при этом силами давления. Силы давления, действующие на боковую поверхность трубки тока перпендикулярно к перемещению, работы не совершают. При перемещении границы MN в положение силами давления совершается работа , где – величина перемещения. Эту работу можно представить в виде или , где 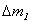– масса жидкости в объеме 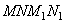, 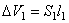. При перемещении границы CD в положение 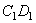жидкость совершает работу против сил давления 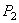. 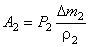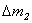Рассуждая аналогично, найдем , где – масса жидкости в объеме .

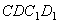Бернулли уравнение, основное уравнение гидродинамики, связывающее (для установившегося течения) скорость текущей жидкости v, давление в ней р и высоту h расположения малого объёма жидкости над плоскостью отсчёта. Б. у. было выведено Д. Бернулли в 1738 для струйки идеальной несжимаемой жидкости постоянной плотности r, находящейся под действием только сил тяжести. В этом случае Б. у. имеет вид:

v²/ 2 + pl r + gh = const,

где g — ускорение силы тяжести. Если это уравнение умножить на r, то 1-й член будет представлять собой кинетическую энергию единицы объёма жидкости, а др. 2 члена — его потенциальную энергию, часть которой обусловлена силой тяжести (последний член уравнения), а др. часть — давлением p. Б. у. в такой форме выражает закон сохранения энергии. Если вдоль струйки жидкости энергия одного вида, например кинетическая, увеличивается, то потенциальная энергия на столько же уменьшается. Поэтому, например, при сужении потока, текущего по трубопроводу, когда скорость потока увеличивается (т.к. через меньшее сечение за то же время проходит такое же количество жидкости, как и через большее сечение), давление соответственно в нём уменьшается (на этом основан принцип работы расходомера Вентури).

Из Б. у. вытекает ряд важных следствий. Например, при истечении жидкости из открытого сосуда под действием силы тяжести (рис. 1) из Б. у. следует:

v²/2g = h или

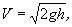
т. е. скорость жидкости в выходном отверстии такова же, как при свободном падении частиц жидкости с высоты h.

Если равномерный поток жидкости, скорость которого v₀ и давление p₀, встречает на своём пути препятствие (рис. 2), то непосредственно перед препятствием происходит подпор — замедление потока; в центре области подпора, в критической точке, скорость потока равна нулю. Из Б. у. следует, что давление в критической точке p ₁ = p ₀ + r v ²₀/2. Приращение давления в этой точке, равное p ₁ - p ₀ = r v ²₀/2, называется динамическим давлением, или скоростным напором. В струйке реальной жидкости её механическая энергия не сохраняется вдоль потока, а расходуется на работу сил трения и рассеивается в виде тепловой энергии, поэтому при применении Б. у. к реальной жидкости необходимо учитывать потери на сопротивление.

Б. у. имеет большое значение в гидравлике и технической гидродинамике: оно используется при расчётах трубопроводов, насосов, при решении вопросов, связанных с фильтрацией, и т.д. Бернулли уравнение для среды с переменной плотностью р вместе с уравнением неизменяемости массы и уравнением состояния является основой газовой динамики.

Date: 2015-05-04; view: 1060; Нарушение авторских прав