
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Внутреннее трение
|
|
Явление внутреннего трения с макроскопической точки зрения связано с возникновением сил трения между слоями газа или жидкости, перемещающимися параллельно друг другу с различными по величине скоростями. Со стороны слоя, движущегося быстрее, на более медленно движущийся слой действует ускоряющая сила. Наоборот, медленно перемещающийся слой тормозит более быстро движущиеся слои газа. Силы трения, которые при этом возникают, направлены по касательной к поверхности соприкосновения слоев.
Рассмотрим известный опыт Ньютона. Пусть имеются две параллельные пластинки (рис. 1), между которыми находится газ (жидкость).
Расстояние между пластинками h. Нижнюю пластинку будем удерживать неподвижно, верхнюю заставим двигаться в одном и том же направлении в своей плоскости с постоянной скоростью u0. Слой газа, непосредственно прилегающий к верхней пластинке, будет иметь ту же скорость u0, что и пластинка, слой же газа, прилегающий к нижней пластинке, находится в покое. Как показывает опыт, любой промежуточный слой движется со скоростью u, пропорциональной расстоянию x от неподвижной пластинки, т. е.
Постоянная a определяется из условия, что при x = h u = u0, т. е. u0 = ah. Откуда a = u0/h. Тогда выражение (3.3.1) примет вид
Таким образом, к верхней пластинке приложена сила F1, лежащая в ее плоскости и имеющая то же направление, что и направление движения пластинки. Так как пластинка движется с постоянной скоростью u0, то на пластинку должна действовать такая же по величине, но противоположно направленная сила F со стороны газа, которую назовем силой вязкого трения. Из опыта следует, что абсолютная величина силы F1 пропорциональна скорости u0, с которой мы двигаем пластинку, и площади пластины, т. е.
где
Так как из (3.3.2) следует, что
Это закон внутреннего вязкого трения Ньютона, который установил его экспериментально. Закон утверждает: при стационарном (ламинарном) движении слоев жидкости или газа с различными скоростями между ними возникают касательные силы, пропорциональные градиенту скорости слоев и площади их соприкосновения. Физический смысл коэффициента вязкости Согласно второму закону Ньютона,
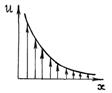
Пусть изменение скорости движения газа или жидкости происходит в направлении оси X, а сама скорость течения направлена перпендикулярно этой оси (рис. 2).
Тогда закон Ньютона (3.3.6) утверждает: импульс, переносимый за время dt через площадку dS, перпендикулярной оси X, пропорционален времени dt, величине площадки dS и градиенту скорости С молекулярно-кинетической точки зрения причиной внутреннего трения является наложение упорядоченного движения слоев газа с различными гидродинамическими скоростями u и хаотического теплового движения молекул. В результате теплового движения, молекулы из более быстрого слоя переносят с собой больший упорядоченный импульс Таким образом, с точки зрения молекулярно-кинетической теории в процесс внутреннего трения каждая молекула переносит упорядоченный импульс
Сравнивая последнее соотношение с (3.3.6), получим формулу для коэффициента вязкости газов:
Из формулы (3.3.8) видно, что коэффициент вязкости газов, как и коэффициент теплопроводности, не зависит от давления. Опыт подтверждает этот вывод. Отклонения наблюдаются при очень низких и очень высоких давлениях, когда Наиболее точные методы измерения коэффициента вязкости основаны на формуле Пуазейля:
где V – объем газа, протекшего за время t через капилляр радиуса r и длины l при разности давлений |
Величина и направление скорости в рассматриваемых точках пространства в общем случае могут меняться со временем. Если ни в одной из точек потока вектор скорости υ течением времени не изменяется, то течение жидкости называется установившимся или стационарным. Но в разных точках стационарного потока скорости могут быть различными. Это означает, что линии тока при установившемся течении жидкости совпадают с траекториями частиц
Неразрывности уравнение
фундаментальное уравнение аэро- и гидродинамики, выражающее в дифференциальной форме закон сохранения массы в потоке:
d(()/dt + div((()V) = 0,
где (г) — плотность, t — время, V — вектор скорости потока.
Впервые Н. у. было получено Л. Эйлером (1755), рассматривавшим баланс расхода жидкости через элементарный объём в предположении, что в потоке сплошной среды отсутствуют источники или стоки массы. Это уравнение равносильно утверждению, что в достаточно малой окрестности любой точки течения изменения плотности вещества и потока массы через эту окрестность равны по численному значению и противоположны по знаку.
Поле течения, описываемое этим уравнением, называют трубчатым, или соленоидальным. Н. у. в дифференциальной форме справедливо всюду за исключением точек, линий или поверхностей, где плотность или скорость терпят разрыв. В этом случае Н. у. должно использоваться в интегральной форме. Н. у. замыкает Навье — Стокса уравнения,
Пове́рхностное натяже́ние — термодинамическая характеристика поверхности раздела двух находящихся в равновесии фаз, определяемая работой обратимого изотермокинетического образования единицы площади этой поверхности раздела при условии, что температура, объём системы и химические потенциалы всех компонентов в обеих фазах остаются постоянными.
Поверхностное натяжение имеет двойной физический смысл — энергетический (термодинамический) и силовой (механический). Энергетическое (термодинамическое) определение: поверхностное натяжение — это удельная работа увеличения поверхности при её растяжении при условии постоянства температуры. Силовое (механическое) определение: поверхностное натяжение — это сила, действующая на единицу длины линии, которая ограничивает поверхность жидкости[1].
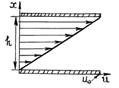
Сила поверхностного натяжения направлена по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует и пропорциональна длине этого участка. Коэффициент пропорциональности 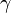 — сила, приходящаяся на единицу длины контура — называется коэффициентом поверхностного натяжения. Он измеряется в ньютонах на метр. Но более правильно дать определение поверхностному натяжению, как энергии (Дж) на разрыв единицы поверхности (м²). В этом случае появляется ясный физический смысл понятия поверхностного натяжения.
— сила, приходящаяся на единицу длины контура — называется коэффициентом поверхностного натяжения. Он измеряется в ньютонах на метр. Но более правильно дать определение поверхностному натяжению, как энергии (Дж) на разрыв единицы поверхности (м²). В этом случае появляется ясный физический смысл понятия поверхностного натяжения.
Date: 2015-05-04; view: 949; Нарушение авторских прав
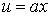
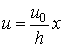

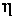 – постоянный коэффициент пропорциональности, который называют коэффициентом вязкого трения. Учитывая, что сила вязкого трения
– постоянный коэффициент пропорциональности, который называют коэффициентом вязкого трения. Учитывая, что сила вязкого трения 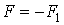 , равенство (3.3.3) перепишем в виде
, равенство (3.3.3) перепишем в виде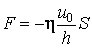
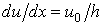 , то последнее выражение можно представить так:
, то последнее выражение можно представить так: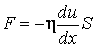
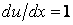 .
.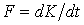 , где K – импульс элементарной массы слоя газа. Поэтому (3.3.5) можно представить в виде бесконечно малых:
, где K – импульс элементарной массы слоя газа. Поэтому (3.3.5) можно представить в виде бесконечно малых:
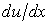 . Знак “минус” означает, что импульс переносится в направлении уменьшения скорости слоя.
. Знак “минус” означает, что импульс переносится в направлении уменьшения скорости слоя.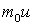 и, сталкиваясь, передают его молекулам более медленно движущегося слоя, вследствие чего он увеличивает скорость. Наоборот, при переходе молекул из медленно движущегося слоя в более быстрый слой, они приносят в него меньший упорядоченный импульс, что приводит к уменьшению упорядоченной скорости этого слоя. Увеличение или уменьшение гидродинамической скорости слоя газа, согласно второму закону динамики, свидетельствует о наличии силы внутреннего трения, действующей между слоями. Следовательно, за счет теплового хаотического движения скорости слоев будут выравниваться, если, конечно, внешними силами не поддерживать разности скоростей слоев.
и, сталкиваясь, передают его молекулам более медленно движущегося слоя, вследствие чего он увеличивает скорость. Наоборот, при переходе молекул из медленно движущегося слоя в более быстрый слой, они приносят в него меньший упорядоченный импульс, что приводит к уменьшению упорядоченной скорости этого слоя. Увеличение или уменьшение гидродинамической скорости слоя газа, согласно второму закону динамики, свидетельствует о наличии силы внутреннего трения, действующей между слоями. Следовательно, за счет теплового хаотического движения скорости слоев будут выравниваться, если, конечно, внешними силами не поддерживать разности скоростей слоев.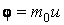 , вызывая тем самым изменение импульса слоя. Подставляя в общее уравнение переноса (4.4.7)
, вызывая тем самым изменение импульса слоя. Подставляя в общее уравнение переноса (4.4.7) 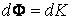 , получим:
, получим: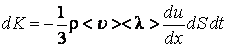
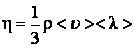
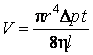
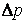 на его концах. Измерив в опыте все указанные величины, из формулы Пуазейля находят коэффициент вязкости
на его концах. Измерив в опыте все указанные величины, из формулы Пуазейля находят коэффициент вязкости