
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

V. Продолжение работы по теме урока. – Прочитайте условие задачи
|
|
1. В ы п о л н е н и е задания № 471.
– Прочитайте условие задачи.
– Что известно? Прочитайте вопрос.
– Решите задачу. (Для двух цветных карандашей требуется достать 12 карандашей, для трех простых – 7 карандашей.)
– Измените данные задачи так, чтобы для получения трех простых карандашей потребовалось достать больше карандашей, чем для получения двух цветных. (Достаточно поменять местами данные «10 цветных» и 4 «простых карандаша».)
2. В ы п о л н е н и е задания на с. 159.
– Учащиеся выполняют математический фокус.
Примечание.
Секрет фокуса в том, что при любом задуманном числе после отбрасывания всех цифр кроме единиц остается 5, а значит, результат последнего умножения всегда 25, сумма цифр которого равна 7.
Рассмотрим последовательно все шаги фокуса. Любое натуральное число при умножении на 2 дает четное число. Сумма четного числа и единицы всегда число нечетное. Значение произведения нечетного числа на 5 оканчивается цифрой 5. О дальнейшем сказано выше.
Помимо римской нумерации, знакомство с которой начинается во втором классе, желательно познакомить учеников еще хотя бы с одной системой записи чисел, которая использовалась до того, как появилась современная система, которой пользуются в настоящее время.
Одним из вариантов может явиться рассмотрение нумерации, которая использовалась в России до эпохи Петра 1. Она интересна как с точки зрения получения исторических знаний о нашей стране, так и с точки зрения того, что относится к алфавитным системам записи чисел, которые были достаточно широко распространены в мире.
Принцип алфавитной системы нумерации заключается в использовании для записи чисел не специальных знаков-цифр, а букв того алфавита, которым пользуется народ, с добавлением определенных знаков, которые позволяют отличать записи чисел от других записей теми же буквами. В период распространения алфавитной записи чисел на Руси использовался старорусский алфавит, буквами которого записывались числа. Отличительным знаком того, что записано число, являлся знак «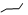 », который назывался титло.
», который назывался титло.
Первые 9 букв обозначали числа от 1 до 9, следующие 9 – круглые десятки от 10 до 90, следующие 9 – круглые сотни от 100 до 900. Таким образом, буквы алфавита позволяли записать все однозначные, двузначные и трехзначные числа. При этом буквы записывались в том порядке, в каком назывались разряды числа. Например, для всех двузначных чисел, больших 20, сначала записывалась буква, обозначающая число десятков, а справа от нее буква, обозначающая число единиц. Для двузначных чисел второго десятка сначала писалась буква, обозначающая число единиц, а затем буква, обозначающая один десяток.
Приводим буквы старорусского алфавита и их числовые значения:

|
Практическую работу, связанную со знакомством с данной системой нумерации не следует проводить на основе использования незнакомого детям старорусского алфавита. Значительно проще и понятнее будет использование нашего современного алфавита. Поскольку в нем 33 буквы, а требуется только 27, оказывается возможным исключить часть букв. Мы предлагаем исключить буквы Ё, Й, Щ, Ъ, Ь, Ы.
В этом случае получим: 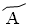 – 1,
– 1, 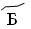 – 2,
– 2, 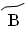 – 3,
– 3, 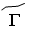 – 4,
– 4, 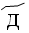 – 5,
– 5, 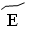 – 6,
– 6, 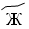 – 7,
– 7, 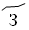 – 8,
– 8, 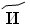 – 9,
– 9, 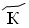 – 10,
– 10,  – 20,
– 20, 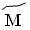 – 30,
– 30, 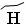 – 40,
– 40, 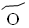 – 50,
– 50, 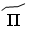 – 60,
– 60, 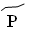 – 70,
– 70, 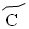 – 80,
– 80, 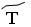 – 90,
– 90, 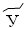 – 100,
– 100, 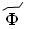 – 200,
– 200, 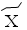 – 300,
– 300, 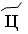 – 400,
– 400, 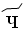 – 500,
– 500, 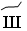 – 600,
– 600, 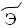 – 700,
– 700, 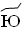 – 800,
– 800, 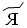 – 900.
– 900.
Приведем примеры записи разных чисел при помощи закрепленных значений букв, обозначенных выше:
11 = 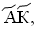 15 =
15 = 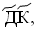 19 =
19 = 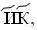 28 =
28 = 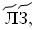 54 =
54 = 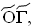 87 =
87 =  396 =
396 = 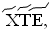 707 =
707 = 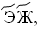 518 =
518 = 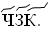
В третьем классе в течение практически всего учебного года можно ограничиться только изложенным выше материалом, предлагая задания на написание чисел до 999 при помощи современных букв русского алфавита и принципов алфавитной русской нумерации, изложенных выше, а также задания, которые предлагают перевести буквенную запись в запись при помощи современных цифр десятичной системы.
Только в конце третьего класса дети могут познакомиться с записью чисел, больших 999. Для этого наши предки использовали те же буквы, но добавляли к ним не титло, а другие значки. Так, если буква А должна обозначать не единицу, а одну тысячу, слева внизу от нее ставился знак «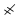 », который обозначал слово тысяча. Таким образом, те же 9 букв с новым знаком позволяли записать все числа, содержащие единицы тысяч.
», который обозначал слово тысяча. Таким образом, те же 9 букв с новым знаком позволяли записать все числа, содержащие единицы тысяч.
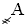 – 1 000,
– 1 000, 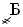 – 2 000,
– 2 000, 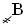 – 3 000,
– 3 000, 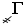 – 4 000,
– 4 000, 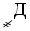 – 5 000,
– 5 000, 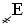 –
–
6 000, 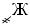 – 7 000,
– 7 000, 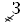 – 8 000,
– 8 000, 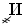 – 9 000.
– 9 000.
Десятки тысяч обозначались этими же девятью буквами, но обведенными кружком. Один десяток тысяч назывался тьма.
 – 10 000,
– 10 000,  – 20 000,
– 20 000,  – 30 000,
– 30 000,  – 40 000,
– 40 000,  – 50 000,
– 50 000,  – 60 000,
– 60 000,  – 70 000,
– 70 000,  – 80 000,
– 80 000,  – 90 000.
– 90 000.
Сотни тысяч обозначали теми же девятью буквами, но кружок вокруг них проводили пунктирной линией. Одна сотня тысяч называлась легион.
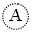 – 100 000,
– 100 000, 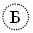 – 200 000,
– 200 000,  – 300 000,
– 300 000,  – 400 000,
– 400 000,  –
–
500 000,  – 600 000,
– 600 000,  – 700 000,
– 700 000,  – 800 000,
– 800 000,  – 900 000.
– 900 000.
Единицы миллионов обозначались теми же буквами, но кружок вокруг них составляли из черточек. Один миллион носил название леодр.
 – 1 000 000,
– 1 000 000, 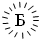 – 2 000 000,
– 2 000 000, 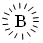 – 3 000 000,
– 3 000 000,
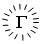 – 4 000 000,
– 4 000 000,  – 5 000 000,
– 5 000 000, 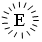 – 6 000 000,
– 6 000 000,
 – 7 000 000,
– 7 000 000,  – 8 000 000,
– 8 000 000,  – 9 000 000.
– 9 000 000.
Запишем, например, в описанной системе число 7 589 326.
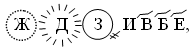
которое читается так: семь леодров пять легионов восемь темь 9 тысяч триста двадцать шесть.
Описанная выше нумерация называлась малое число. Но существовала еще нумерация, которая называлась большоечисло или великое число.
В отличие от описанной системы малого числа, в которой счет велся только в пределах единиц миллионов, система большого или великого числа позволяла записывать числа в пределах 49-значных чисел в современной системе счисления. Эта система интересна также тем, что названия больших чисел строились по принципу «столько раз по столько».
В этой системе не число 10 000, а число 1 000 000 называлось тьма (обозначалась буквой в круге).
Затем число, в котором тьма I взята тьму раз (1 000 000 000 000), называлось легион (обозначался буквой в круге из точек), легион легионов образовывал леодр (обозначался буквой в круге из черточек), леодр леодров образовывал ворон (обозначался буквой в круге из крестиков). Десять воронов образовывали колоду (она обозначалась как А). На этом числе счет окончательно прекращался. Как написано в рукописи XVII века «... и более сего несть человеческому разуму разумевати».
Приведем соответствующие записи основных больших чисел системы великого числа:
 – тьма – 1 000 000,
– тьма – 1 000 000,
 – легион – 1 000 000 000 000,
– легион – 1 000 000 000 000,
 – леодр – 1000 000 000 000 000 000 000 000,
– леодр – 1000 000 000 000 000 000 000 000,
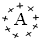 – ворон – 1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000,
– ворон – 1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000,
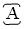 – колода – 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
– колода – 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
Объем материала, который будет использован в работе с учениками, форма его использования (включение в уроки, использование на занятиях математического кружка или в группе особо заинтересовавшихся детей и т. д.) полностью определяет учитель.
В а р и а н т ы з а д а н и й:
1) Построение самой системы (желательно, чтобы дети сами соотнесли единицы, десятки и сотни с соответствующими буквами алфавита на основе общего разъяснения со стороны учителя и обсуждения вопроса о необходимом количестве букв).
2) Запись чисел, данных в современной записи, при помощи алфавитной системы (в основном используются двузначные и трехзначные числа, работа с большими числами проводится только по желанию самих учеников).
3) Переход от алфавитной записи чисел к современной нумерации (числовой уровень таких заданий аналогичен уровню, описанному в предыдущем пункте).
4) Обязательным компонентом знакомства с алфавитной русской системой нумерации является ее сравнение с римской и современной системами. Особенно важно сравнение с современной системой, которой пользуются ученики, так как это наглядно покажет ее совершенство и красоту, что и является одной из главных целей знакомства с любыми другими системами записи чисел.
Алфавитные системы нумерации были широко распространены в мире. Ими пользовались греки, от которых наши предки и позаимствовали эту систему вместе с православием, арабы, грузины, армяне, евреи. В России алфавитная система существовала до 1703 года, когда вместе с реформами Петра I в страну пришла десятичная позиционная система.
Date: 2015-06-08; view: 1598; Нарушение авторских прав