Бюджетная линия. Если для анализа желаний потребителя используются кривые безразличия, то для анализа его возможностей — бюджетные линии

Если для анализа желаний потребителя используются кривые безразличия, то для анализа его возможностей — бюджетные линии. Будем по-прежнему оперировать потребительским набором из двух благ X и Y, предполагая, что индивид расходую полностью свой доход на их покупку. Введем обозначения:

М — денежный доход потребителя, р.

X, Y — количества покупаемых товаров, един.

Рг Ру — цены товаров X и Y, р.

Тогда математическая модель бюджетного ограничения выглядит следующим образом:

M = P_X X + P_Y Y (1)

Ограничение покупательной способности потребителя величиной его денежного дохода называется бюджетным ограничением.

Все доступные потребителю при данном доходе и данных ценах наборы товаров X и Y представлены точками, находящимися на бюджетной линии.

Бюджетная линия – это линия, отображающая множество вариантов набора из двух благ, приобретение которых требует одинаковых денежных затрат .

Для того чтобы построить бюджетную линию, выведем на основе уравнения (1) уравнение бюджетной линии:

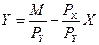(2)

Очевидно, что мы имеем уравнение типа у = а — bx, которое выражает прямую линию с отрицательным наклоном.

Предположим, что доход потребителя Тани составляет 240 р. Она покупает апельсины (товар Y) и яблоки (товар X Цена одного килограмма апельсинов равна 30 р, а цена одного килограмма яблок — 24 р.

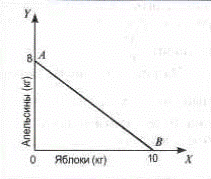
Рис. 8 Бюджетная линия

При доходе в 240 р. и цене апельсинов и яблок соответственно 30 и 24 р.бюджетная линия АВ показывает комбинации этих благ, которые Таня может позволить себе купить.

В этом случае уравнение бюджетной линии имеет такой вид:

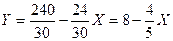
Построим данную бюджетную линию (см. рис. 8).

Бюджетная линия АВ ограничивает пространство ОАВ, представляющее собой множество точек, каждая из которых означает набор двух товаров, доступных потребителю. Но лишь точки, расположенные на бюджетной линии, выражают наборы, при покупке которых доход тратится без остатка. Точки, лежащие за пределами бюджетной линии, отражают наборы, недоступные потребителю.

Значение свободного члена уравнения бюджетной линии (I/ P_У) показывает длину отрезка вертикальной оси от начала системы координат до пересечения с бюджетной линией (ОА). Экономический смысл этой величины — количество единиц товара Y, которое может купить потребитель, при условии, что он весь доход будет тратить на приобретение данного товара. Это —реальный доход потребителя, выраженный в единицах товара Y.

Коэффициент 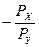при независимой переменной X показывает наклон бюджетной линии, отражающий отношение цен товаров X и Y, т.е. степень их доступности для потребителя.

Очевидно, что длина отрезка ОВ показывает то количество единиц товара X, которое Таня может купить, если она будет направлять весь доход на приобретение только данного товара, т. е. реальный доход потребителя, выраженный в яблоках, составит M/Р_Х

На рис. 8 показано, что Таня может купить на свой денежный доход 8 кг апельсинов (240: 30) или 10 кг яблок (240:24), если она будет тратить весь свой доход на потребление одного из этих товаров.