
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Взаимодействие с веществом альфа-излучения
|
|
Альфа-частицы относят к тяжёлым частицам (наряду с протонами, нейтронами, дейтронами и тритонами). Собственно, α-частицы представляют собой ядра атомов гелия и состоят из двух протонов и двух нейтронов, т.е. имеют атомную массу 4 и заряд 2. В этой группе частиц массы различаются не более чем в 4 раза, а заряды – в 2 раза. Поэтому могут быть установлены точные соотношения между величинами пробегов, линейными коэффициентами ослабления и другими характеристиками взаимодействия этих частиц с веществом. Поэтому достаточно рассмотреть взаимодействие с веществом альфа-частиц, а для остальных тяжёлых заряженных частиц существуют пересчётные формулы для определения характеристик их взаимодействия с веществом, учитывающие различие их масс и зарядов по сравнению с альфа-частицами.
Известно большое число радиоактивных изотопов, при распаде которых образуются α-частицы. Их энергия зависит от того, каким радиоактивным веществом они испускаются, и не превышает 9 МэВ. Более высокие энергии альфа-частиц (до десятков гигаэлектрон-вольт) могут быть получены в ускорителях заряженных частиц..
Двигаясь в веществе, α-частицы испытывают электрические взаимодействия с электронами атомов, в процессе которых постепенно теряют свою энергию, после чего, присоединяя к себе электроны, нейтрализуются, образуя атомы гелия. Атомные электроны, получив от α-частицы во время столкновения порцию энергии, либо вырываются из атома, либо переходят на более высокую орбиту, т.е. α-частица вдоль своей траектории движения производит ионизацию и возбуждение атомов вещества. При этом число возбуждённых атомов в несколько раз превышает число ионизированных.
При полном замедлении α-частицы суммарная потеря энергии на ионизацию Е1 и возбуждение Е2 атомов равна начальной кинетической энергии α-частицы:
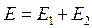 . (3.22)
. (3.22)
Если в процессе замедления α-частицы возникло N ионных пар, то средняя энергия, затрачиваемая α-частицей в веществе на образование одной ионной пары, будет равна
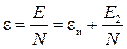 . (3.23)
. (3.23)
Величину ε называют энергией образования ионной пары. Она больше энергии ионизации атома εи = Е 1 /N примерно в два раза. Чтобы найти число ионных пар, возникающих при полном торможении частицы в веществе, необходимо кинетическую энергию α-частицы разделить на соответствующее значение ε. В таблице 3.5 [3] представлены значения энергии образования ионной пары и энергии ионизации для некоторых чистых газов.
Таблица 3.5
Энергия образования ионной пары ε и энергия ионизации εи
некоторых чистых газов
| Газ | ε, эВ | εи , эВ | Газ | ε, эВ | εи , эВ | |
| He Ne Ar Kr Xe H2 CO2 | 42,7 36,8 26,4 24,1 21,9 36,3 34,5 | 24,56 21,56 15,76 14,00 12,13 15,43 13,73 | O2 N2 CH4 C2H2 C2H6 C2H4 Воздух | 32,5 36,6 29,2 27,5 26,6 28,0 35.5 | 12,20 15,51 13,04 11,35 11,76 10,51 - |
При небольших энергиях α-частицы начинается её «перезарядка». Сравнительно медленно пролетая рядом с электроном, она может захватить его, в результате чего её заряд уменьшается на единицу. Однако в последующих столкновениях, она вновь теряет его. В результате таких перезарядок ионизация атомов возрастает, а сама частица быстрее тормозится. Зависимость изменения удельной ионизации от пройденного в веществе пути ионизирующей частицей иллюстрируется кривой Брэгга, представленной на рисунке 3.17- а, а зависимость плотности потока от пройденного в веществе пути – на рисунке 3.17- б [3].
Пик на кривой Брэгга объясняется особенностями взаимодействия медленных α-частиц с атомными электронами. Чем медленнее движется α-частица, тем больше время её взаимодействия с атомными электронам, а следовательно, и вероятность ионизации атома. Но когда начинается процесс перезарядки, α-частица резко тормозится, её энергия падает и вероятность ионизации также резко падает. Затем α-частица, исчерпав свою энергию, останавливается и нейтрализуется. Поскольку масса α-частицы в тысячи раз больше массы электронов, то при столкновениях с электронами она практически не отклоняется от направления своего первоначального движения и её траектория представляет собой прямую линию. Расстояние, проходимое α-частицей от источника до остановки, называют линейным пробегом R.

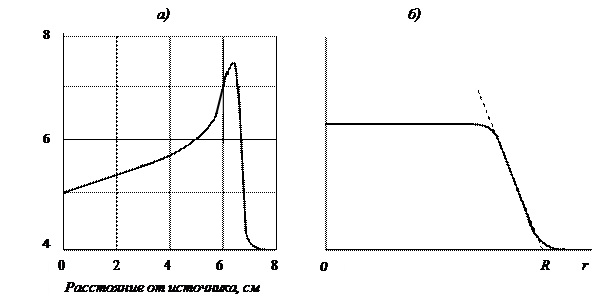

Рис. 3.17. Изменение удельной ионизации при торможении α-частицы
в воздухе (кривая Брэгга) – а, и зависимость потока α-частиц от расстояния до источника – б (R – экстраполированный пробег, R 0 – средний пробег)
Некоторый разброс в пробегах моноэнергетических α-частиц объясняется вероятностным характером их взаимодействия с электронами атомов. Частицы теряют свою энергию в большом, но конечном числе актов столкновений. Флуктуациям подвержено как число таких актов на единицу пути, так и потери энергии в каждом акте. Поэтому за величину линейного пробега принимают либо средний пробег R 0 , либо экстраполированный линейный пробег R, который близок к максимальному пробегу (см. рис. 3.17- б). Разница между экстраполированным и средним пробегами называется разбросом пробегов: δ = R – R 0. Величина разброса составляет примерно 1 % от экстраполированного пробега при энергии α-частиц 5 МэВ.
Альфа-излучение обладает существенно более сильным ионизирующим действием, чем β-излучение, вследствие существенно большей массы и энергии α-частиц. Поэтому глубина проникновения альфа-излучения в вещество существенно меньше.
Глубиной проникновения считается толщина слоя поглотителя, при прохождении через который интенсивность излучения ослабляется в е раз.
Она также зависит от энергии α-частиц и для воздуха при температуре +15 0С и давлении 101,3 кПа её можно подсчитать по эмпирической формуле [3]:
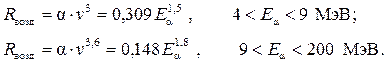 (3.24)
(3.24)
где глубина проникновения R определяется в см, а энергия Е – в МэВ.
При энергии α-частиц в 10 МэВ глубина проникновения в воздухе составляет около 10 см. В твёрдых веществах глубина проникновения α-излучения составляет доли или единицы мм.
Соотношение между пробегом и энергией α-частиц в различных веществах широко изучалось как теоретически, так и экспериментально. С хорошей точностью пробег α-частиц в веществе с атомным номером А можно рассчитать по эмпирической формуле [14]
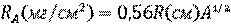 , (3.25)
, (3.25)
где R – пробег α-частиц в воздухе при температуре +150 С и давлении 760 мм рт. ст. (101,3 кПа), который находится по формулам (3.24).
Пробег частиц в различных веществах можно выразить через пробег в воздухе при помощи так называемой относительной тормозной способности. Она представляет собой отношение тормозной способности данного вещества к тормозной способности воздуха.
Тормозная способность выражается либо в виде потери энергии частицы на единице пути – линейная тормозная способность, либо в виде потери энергии частицы на единице толщины, выраженную через массу, приходящуюся на единицу площади – массовая тормозная способность.
Абсолютные тормозные способности для любого вещества очень сильно зависят и от вида частиц и от их энергии. Использование относительной тормозной способности позволяет в значительной степени ослабить зависимости от вида и энергии частиц. Это видно и из приведенной ниже таблицы 3.6 [14], где приведены относительные тормозные способности (линейная SL и массовая Sm) нескольких металлов для α-частиц различной энергии и пробег тех же частиц в воздухе.
Таблица 3.6
Относительные тормозные способности некоторых материалов
для α-частиц различных энергий
| Энергия частицы. МэВ | Пробег в воздухе, см | Al, ρ = 2,7 г/см3 | Cu, ρ = 8,9 г/см3 | Pb, ρ = 11,0 г/см3 | |||
| SL | Sm | SL | Sm | SL | Sm | ||
| 2,0 | 0,80 | - | - | 0,32 | |||
| 6,3 | 0,79 | 0,58 | 0,33 | ||||
| 9,7 | 0,81 | 0,59 | 0,35 | ||||
| 0,86 | 0,65 | 0,39 |
Из неё следует, что если пробег α-частиц в воздухе (а значит и абсолютная линейная тормозная способность воздуха) при изменении энергии α-частиц от 2 МэВ до 37 МэВ изменяется в 100 раз, то относительные тормозные способности для указанных материалов (особенно массовая) при том же диапазоне изменения энергии α-частиц изменяются всего в пределах 10 процентов. Таким образом, относительную тормозную способность удобно использовать именно как характеристику вещества при взаимодействии с ионизирующими излучениями.
Если известно соотношение между пробегом и потерями энергии для данного вида частиц в данном веществе, то можно получить расчётным путём соответствующее соотношение для другого типа частиц в том же веществе. Для этого можно воспользоваться аналитическим выражением тормозной способности материала, определяющим потери энергии частицей на единице пути dE/dx в данном материале:
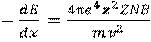 , (3.26)
, (3.26)
где Е – кинетическая энергия частицы;
z – её заряд;
v – её начальная скорость;
N – число атомов в 1 см3 поглотителя;
Z – атомный номер поглотителя;
B – коэффициент торможения;
е – заряд электрона;
m – масса электрона.
Для частицы массой М и зарядом z, используя (3.19), можно найти расстояние, пройденное в данном веществе, на котором её энергия изменится от начальной энергии Е до нуля:
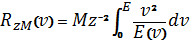 , (3.27)
, (3.27)
С помощью уравнения (3.27) можно найти пробег протонов Rp (v) с начальной скоростью v через пробег α-частиц в том же веществе с той же начальной скоростью:
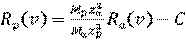 . (3.28)
. (3.28)
Постоянная С здесь введена для учёта процесса захвата и потери электронов (процесса «перезарядки») при малых энергиях. Это связано с тем, что протоны и α-частицы имеют различные заряды, а потому различным образом взаимодействуют с атомными электронами. Экспериментально было найдено, что величина С для воздуха при нормальных температуре и давлении для энергий больших 0,5 МэВ равна 0,20 см. С уменьшением энергии величина С плавно уменьшается и при 6,7 кэВ достигает величины 0,02 см.
Таким образом, для воздуха и для энергий больших 0,5 МэВ можно записать
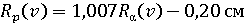 , (3.29)
, (3.29)
а т.к. при равных скоростях частиц для их энергий справедливо соотношение
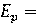 E α Mp /Mα, то вместо (3.29) можно записать
E α Mp /Mα, то вместо (3.29) можно записать
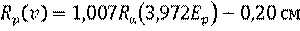 . (3.30)
. (3.30)
Здесь 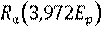 означает пробег α-частицы, рассчитанный для энергии, равной 3,972 от соответствующей энергии протона.
означает пробег α-частицы, рассчитанный для энергии, равной 3,972 от соответствующей энергии протона.
Если нужно найти пробег частицы с таким же зарядом, но с другой массой (например, дейтронов или тритонов по отношению к протонам), то поправочный коэффициент С в выражении (3.28) исчезает, т.к. процесс захвата и потери атомарных электронов у этих частиц протекает одинаково. Поэтому, если известен пробег частицы массой М 0 в веществе, то рассчитать пробег в этом веществе другой частицы с таким же зарядом, но другой массой М, можно по формуле
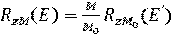 , (3.31)
, (3.31)
где 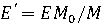 .
.
Date: 2015-06-08; view: 2546; Нарушение авторских прав