Потери напора по длине нефтепровода

Как уже отмечалось, движение любой жидкости (в том числе и нефти) в трубопроводе подчиняется формуле Бернулли (2.2). Отметим сначала некоторые особенности уравнения (2.2) при­менительно к напорному трубопроводу одного диаметра, выпол­ненному из одного материала. Поскольку условия протекания жидкости на каждой единице длины таких труб будут одина­ковы, то потери напора на трение будут также одинаковы. Линия гидравлического уклона будет прямой. Поскольку дви­жение жидкости в трубопроводе будет равномерным, то скорость ее движения будет одинаковой по всей длине, т. е. v ²/(2g) = const.

Это означает, что линия 0₂0₂ (см. рис. 2.1), называемая ли­нией пьезометрического напора, будет по всей длине парал­лельна линии полного напора 0₁0₁, учитывающей не только на­пор p /ρ, создаваемый за счет избыточного давления, но и ско­ростной напор v ²/2g. Соответственно отрезок 0₂0₂' будет равен отрезку 0₁0₁' = h_r, т. е. падение (пьезометрической линии 0₂0₂ будет таким же, как и падение напорной линии 0₁0₁.

Как известно из курса гидравлики, потеря напора от тре­ния по длине трубопровода является функцией нескольких вели­чин: так называемого гидравлического сопротивления, характе­ризуемого коэффициентом λ, длины l и диаметра D_BH трубопровода, скорости течения жидкости – и определяется по формуле Дарси—Вейсбаха

Рассмотрим одну из важнейших особенностей течения жидко­сти по трубопроводу, определяющую гидравлический режим трубопровода при заданных пропускной способности Q, длине l и внутреннем диаметре D _вш трубопровода.

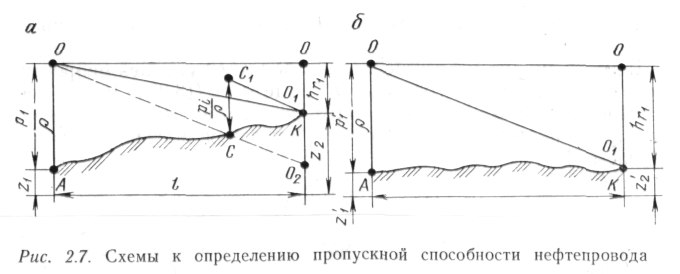
Пусть заданы два продольных профиля участков местности, по которым должны быть проложены трубопроводы одинакового диаметра из точки А в точку К (рис. 2.7). Давление, создавае­мое на выходе из НС, одинаково на обоих трубопроводах и равно р. Давление в точке К — атмосферное, т. е. р₂ = 0. Если бы перекачивалась идеальная жидкость, то линия гидравличо ского уклона в обоих случаях была бы горизонтальной 00. По­скольку нефть является жидкостью реальной, то по длине тру­бопровода происходит уменьшение начального давления р или напора р/ρ, обусловленное потерями напора на трение. Соот­ветственно в обоих случаях линии гидравлического уклона бу­дут иметь вид, изображенный на рис. 2.7 сплошной линией 00₁. По схеме рис. 2.7,6 напор, созданный в начальной точке А, обеспечивает компенсацию потерь напора на трение и всех подъемов рельефа, а по схеме рис. 2.7, а линия гидравличе­ского уклона встречается с линией трубопровода в точке С. Проанализируем этот случай. Чтобы нефть пришла в конечный пункт, потери напора на трение должны быть уменьшены так, чтобы линия гидравлического уклона по крайней мере коснулась точки К (линия 00₁ на рис. 2.7, а). В соответствии с (2.2)

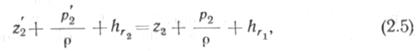
так как по условию p₂ = p₂' = 0, то из (2.5)

Поскольку z₂—z₂'>0, то h_r2>h_r1

Обратимся теперь к формуле (2.4). При одинаковых (в со­ответствии с принятыми исходными данными) λ, l, D_BH

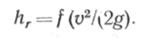
Следовательно, если по одному трубопроводу (см. рис. 2.7, б) пропускается заданное количество нефти Q со скоростью v₂, то по другому трубопроводу (см. рис. 2.7, а) это количество нефти не пройдет, так как скорость движения ее v ₁ уменьшится из-за преодоления геодезической высоты z₂— z₁. Скорость v _l можно найти по (2.4) при величине h_r1, определяемой из (2.6). Для того чтобы пропустить по первому трубопроводу заданное ко­личество продукта, необходимо увеличить скорость его движе­ния до v_l = v₂. Это можно сделать, создавая соответствующий гидравлический уклон i за счет установки насосной станции в точке С, поднимающей в трубопроводе напор до значения р_i/ρ, при котором линия гидравлического уклона С₁0₁ будет параллельна ОС0₂.

Таким образом, при гидравлическом расчете трубопровода возникают две взаимосвязанные задачи: расстановка НС и определение гидравлического уклона, при которых обеспечива­ется пропуск необходимого количества нефти или нефтепро­дукта.

Приведем основные формулы для определения коэффициента гидравлического сопротивления λ,. Как показано в гидравлике коэффициент λ, зависит от режима течения: ламинарного или турбулентного. При ламинарном (струйном) течении λ, определяется по Стоксу: λ = 64/Re, где Re— критерий Рейнольдса. Ламинарный режим сохраняется до Re~2320; при 2320<Re<2800 существует так называемый переходный режим. Коэф­фициент λ при этом можно определять по формуле λ = (0,16 Re—13)•10^-4.

При Re>2800, т. е. турбулентном режиме течения, коэффициент К можно определять по формулам, при­веденным в табл. 2.4.

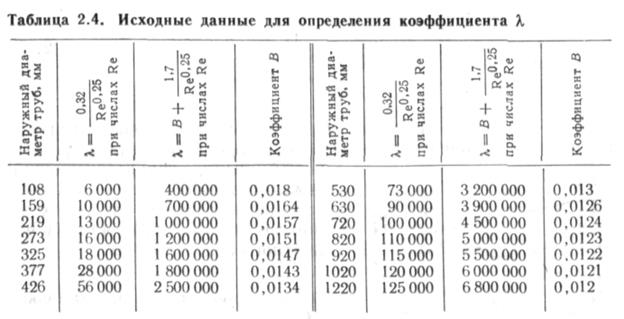
Принечания, При числах Re, больших указанных в таблице, коэффициент λ остается постоянным. Расчетные формулы соответствуют условиям применения цельно­тянутых труб диаметром до 377 мм со средней абсолютной шероховатостью 0,125 мм и свар­ных труб диаметром от 426 мм и более со средней абсолютной шероховатостью 0,1 мм

Date: 2015-06-07; view: 1439; Нарушение авторских прав