Определение числа и расстановка НС

Задача определения числа НС и их расстановка вдоль трубопровода связаны не только с технологическими параметрами, но и с прочностными характеристиками трубопровода. Основной нагрузкой на трубы является внутреннее давление, поэтому тол­щина их стенки определяется в основном этим давлением. Если известна толщина стенки труб δ, то, определив на основании прочностных расчетов внутреннее давление р, можно узнать предельное давление на выходе из каждой НС. Можно посту­пить иначе — задать расчетное давление на выходе из НС, а оп­ределять необходимую толщину стенки труб.

Определение числа НС

Пусть по прочностным характеристикам труба со стенкой δ до­пускает создание в ней внутреннего давления р. Напор, соот­ветствующий этому давлению на выходе из НС:

На входе в НС давление не может быть нулевым. Для нормаль­ной работы насосов головной станции требуется создание под­пора для обеспечения бескавитационной работы первого насоса Δh₁=p₁/ρ.

В конечной точке трубопровода должен быть создан напор h₂, равный высоте продукта в приемном резервуаре. Для упро­щения расчетов h₂ принимают обычно равным нулю. Учитывая сказанное, можно составить уравнение баланса напоров для трубопровода полной длины

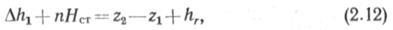
где п — число НС; z₁, z₂ — расстояния от плоскости сравнения (обычно геодезическая отметка) соответственно начальной и ко­нечной точек трубопровода; h_r — потери напора на трение.

Из (2.12) n= (z₂—z₁ + h_r—Δh₁)/H_CT. Если не учитывать Δh₁, то

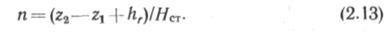
Расстановка насосных станций

По методике, принятой в настоящее время, расстановка НС осу­ществляется так называемым графоаналитическим методом. Оп­ределив гидравлический уклон в трубопроводе по (2.9) или (2.10) и учитывая (2.7), формулу (2.13) можно представить в несколько ином виде: n=(z₂ —z₁ + il)/H_CT.

Далее задача заключается в расстановке п станций по длине l по известному продольному профилю трубопровода.

Пусть задан профиль (рис. 2.9), вдоль которого необходимо расставить насосные станции. Определив (по 2.8) гидравличе­ский уклон, от вертикали, проходящей через концевую точку трассы, строим линии этого уклона (00 и т. д.). Это построение выполняется до тех пор, пока одна из линий не коснется в ка­ком-либо сечении профиля. Такая точка называется перевальной (точка П на рис. 2.9).

Расстояние от начала трубопровода до этой точки называют расчетной длиной трубопровода. За пере­вальной точкой движение нефти осуществляется самотеком, и следовательно, все насосные станции должны быть размещены до перевальной точки. На рис. 2.10 изображен участок профиля за перевальной точкой. Проведя из концевой точки линию i, видим, что для течения нефти на участке достаточен напор, расходуемый на компенсацию потерь на трение, т. е.

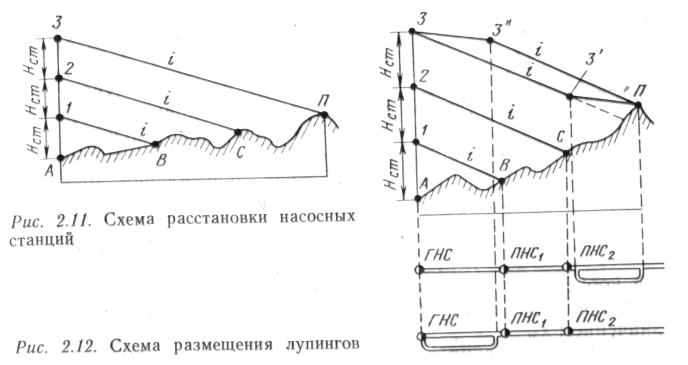
Из рис. 2.12 видно, что напор в точке П больше необходи­мого (2.14) на величину 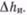Этот избыточный напор на участке трубопровода ПП₁ должен привести к увеличению скорости течения. Так как расход жидкости остается постоянным, то на участке ПП₁ жидкость будет заполнять не все сечение труб. Это подтверждается практикой эксплуатации.

Определив перевальную точку, расставляют НС по методу Шухова. Пусть задан профиль до перевальной точки (рис. 2.11), на котором необходимо разместить три НС. Отложив по верти­кали от точки А З H_СТ, проводим через точки 1, 2, 3 прямые с уклоном i. Допустим, что линия ЗП коснулась перевальной точки; тогда станции следует расставить в точках А, В и С. Однако такой случай встречается редко, чаще число п оказы­вается нецелым. Поэтому приходится ставить либо большее число станций, что экономически невыгодно, либо меньшее, но для компенсации недостающего напора прокладывать лупинги.

На рис. 2.12 показан профиль, на котором по (2.13) должно быть больше трех, но меньше четырех станций. Как и в преды­дущем примере, по вертикали откладываем напор З H_СТ, через точку 3 проводим линию i. Чтобы линия i достигла переваль­ной точки, можно поставить лупинг на участке З'П. Линия ЗЗ'П характеризует падение напора для случая, когда лупинг установлен на перегоне за ПНС2. Если разместить лупинг на начальном участке, то линия напора будет иметь вид 33"П.

Формализация процесса расстановки НС

Графический метод расстановки НС чрезвычайно осложняет получение наилучшего решения задачи о выборе оптимальной трассы. Для использования методов оптимального проектиро­вания при выборе наилучшей трассы необходимо формализо­вать рассмотренный метод таким образом, чтобы НС можно было расстанавливать без графических построений П. П. Бородавкиным и Б. И. Кимом предложен следующий алгоритм оп­ределения числа и расстановки НС, легко реализуемый на ЭВМ. Запишем формулу (2.36) в виде

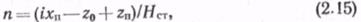
где х_n — координата перевальной точки; z₀, z_n — отметка на­чальной и перевальной точек; H_ст — напор на выходе из НС.

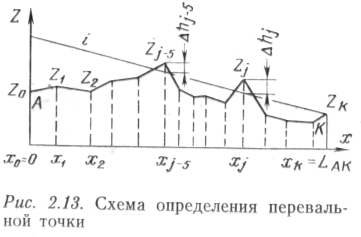
Неизвестными величинами в (2.15) являются х_n и z_n, для определения которых необходимо исследовать профиль трассы нефтепровода на наличие перевальной точки. Рассмотрим произ­вольный профиль трассы длиной l, заданный координатами то­чек излома рельефа местности (рис. 2.13). Проведем из конце­вой точки трубопровода (x_k, z_k) заданную линию гидравличе­ского уклона. Если на профиле имеются перевальные точки, то линия гидравлического уклона пересечет или коснется про­филя трассы.

Из рисунка видно, что возможное превышение каких-либо точек профиля над линией

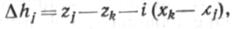
где j = 1, 2, 3,..., k.

Рассмотрим следующие случаи: Δh_j,<0; Δh_jj>0; Δh_j<=0.

В первом случае пере­вальная точка на профиле отсутствует. Отсюда z_n = z_k и х_n = l_АК. Во втором слу­чае перевальная точка на­ходится среди некоторого числа точек с Δh_j>0. Точка с максимальным значением Δh_j и будет перевальной, а ее координаты искомыми величинами. В третьем случае пе­ревальной будет точка с Δh_j= =0 и с минимальным для данного i значением x _j.

Алгоритм решения задачи определения числа НС при про­филе трассы, заданном набором значений

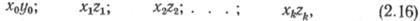
и гидравлическом уклоне i можно описать следующим образом.

Первый шаг. Исключаем из (2.16) все точки с z<=z_k.

Второй шаг. Для х=х_k-1 (если эта точка не исключена) определяем Δh_k-1. Если Δh_k-1, то значения x _k-1, z_k-1 и Δh_k-1 заносим в специальный список (назовем его со) и исклю­чаем из (2.16) точки с с z<=z_k. Если Δh_k-1<0, то исключаем эту точку, а заодно и все точки z<=z из (2.16) и из дальней­шего рассмотрения. Далее для x = x_k-2 (если эта точка уже ис­ключена, то рассматриваем x=x_k-3) определяем Δh_k-2. Анало­гично, если Δh_k-2>0, значения х_k-2, z _k-2 и Δh_k-2 заносим в спи­сок со и исключаем из (2.16) точки с z<=z_k-2. Если Δh_k-2<0, то исключаем эту точку, а вместе с ней и все точки z<=z_k-2 из даль­нейшего рассмотрения. Вычисления выполняем последовательно для всех x ₀<х<х_k.

Третий шаг. Рассматриваем список ω. Если в нем не оказа­лось ни одного значения Δh_j, то х_п = l_АК и z_П = z_k. В противном случае (если в списке со имеются точки с Δh_j>=0) определяем max Δh_j и min x_j, если Δh_j = 0.

Четвертый шаг. Определяем по (2.15) число НС n.

Уравнение линий гидравлического уклона для определения координат любой НС можно представить в виде

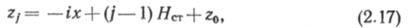
где j — порядковый номер НС; х — текущая координата.

Точки пересечения с профилем трассы и будут искомыми ко­ординатами (координаты первой станции х = х_o, z=z_o).

Число НС (n), определяемое по формуле (2.15), оказыва­ется чаще всего дробным и округляется до ближайшего целого. При округлении числа НС в большую сторону (допустим, до n') необходимо уменьшить напор, приходящийся на каждую станцию, до H'_ст = (n/n')H_ст.

Координаты НС получим, определив точки пересечения линии (2.17) с профилем трассы при H_ст и n'>=j>1.

Рассмотрим случай, когда число НС округлено в меньшую сторону, предположим, до n*. Уменьшение числа НС обычно компенсируют прокладкой лупинга, длина которого Л*. Стои­мость сооружения лупинга, как и основной нитки, зависит от условий местности. Поэтому целесообразно разместить его по трассе так, чтобы стоимость строительства была наименьшей. Вычислим координаты НС по формуле (2.17) при всех n*>=j>1 и обозначим их через x_j, z_j. Прокладка лупинга позволяет изме­нить положение промежуточных НС в некоторых пределах. Для определения границ возможного расположения НС воспользу­емся уравнением.

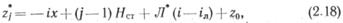
соответствующим размещению лупинга на любом перегоне между НС (здесь i_Л — гидравлический уклон лупинга).

Обозначим точки пересечения линии (2.18) с профилем трассы через х_j*, z_j*. Исследуем далее условия местности на участке прокладки лупинга длиной Л* перед точками x₂*, z₂*, x_з*, z₃*,..., x_n*, z_n* и х_П, z_П. Поскольку величина i _Л<1, то на некоторых участках перед НС может оказаться локальная пе­ревальная точка. В этих случаях для определения стоимости сооружения лупинга необходимо рассматривать участок мест­ности длиной X_jП — х_j, где х_j'— решение уравнения (2.18) и уравнения линий гидравлического уклона, проходящей через локальную перевальную точку (обозначим ее х_jП, z_jП):

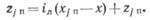
Если для прокладки лупинга выбран участок перед концевой или перевальной точкой трубопровода, то окончательными ко­ординатами НС будут х_j, Zj, а если этот участок выбран перед второй НС, то ее координатами будут х_j*, z _j*. В остальных случаях координаты НС определяются соответствующими рас­четами.

Алгоритм решения задачи расстановки НС при заданном профиле трассы (2.16) и гидравлических уклонах в магистрали и лупинге описывается следующим образом.

Первый шаг. Определяем координаты второй НС по формуле (2.17) при j = 2. Для этого вычисляем Z_2,1 при х = х₁ и сравни­ваем с z₁.

Если Z_2,1<z₁, то, интерполируя Z₂ в интервале x₀<x<x_i, находим х₂ и z₂.

Если Z_2,1=z₁, то вычисляем Z₂,₂ при х=х₂ и сравниваем с z₂. Если Z_2,2<z₂, то х₂ = х₁ и z₂=z₁. Если Z_2,2>z₁ то вычисляем Z₂,₃ при х=х₃ и сравниваем с z₃, и т. д.

Если Z_2,1>z₁, то вычисляем Z_2,2 и сравниваем с z₂. Про­должаем таким образом вычисления для всех х_о<х<х_П до тех пор, пока не найдем х₂ и z₂. Затем при j = 3 и x ₂<х<х_П опре­деляем х₃ и z₃, и т. д.

Второй шаг. Аналогичным образом вычисляем х_j*, z_j* по формуле (2.18).

Третий шаг. Исследуем по исходной информации условия местности на участке длиной Л* перед точками х₂*, z₂*; x _з*, z₃*; х*_п*,, z*_n*, х_П, z_П. Вычисляем стоимости прокладки лупинга на каждом из этих участков и выбираем наилучший, т. е. тот, которому соответствуют наименьшие затраты.

Координатами насосных станций, находящихся до лупинга, будут x₁, z₁; x₂, z₂; x_j*-1, z_j*-1, а для станций, расположенных после лупинга, x_j^*,z_j*,....,x_n**, z_n**, где j* — номер НС, перед которой размещен лупинг.

При целом числе станций или округлении п в большую сто­рону решение заканчивается первым шагом.

Date: 2015-06-07; view: 1308; Нарушение авторских прав