Оптимальная последовательность работ

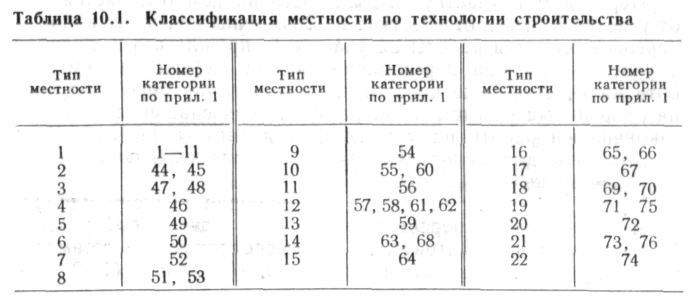
Допустим, что на рассматриваемом участке трассы длиной L имеется п участков длиной /, с характерными признаками, ис­ключающими возможность ведения работ по одинаковой тех­нологии. В числе этих участков имеются и однотипные. Напри­мер, на участке L (рис. 10,2, а) имеются участки // и k' кате­гории 1, /₂², /₆², /ю² категории 2; /₃³, /₈³ категории 3 и т. д. Это означает, что на участках /i и /₅ технология ведения работ оди­накова, на участках 4, /е, ао она одинакова для этих участков, но отлична от технологии ведения работ на участках /i и /_s и т. д. Приведем классификации участков по однотипности вы­полнения работ, используя общую классификацию местности. В горах имеются долины и собственно горы. Долины, имеющие участки с уклонами до 8—10°, относятся к равнинам; на них можно выполнять работы по поточной технологии. На других участках работы выполняют по специальной технологии. Имея это в виду, составим классификацию местности (табл. 10.1). Как видно из таблицы, 1-й тип —равнина —допускает приме­нение обычной технологии. Границы между различными ти­пами местности определяются необходимостью изменения тех­нологии основных работ. Например, возьмем 4-й и 19-й типы: 4-й тип —это продольный уклон до 20° со скальным грунтом, 19^:й тип — косогор с продольным уклоном до 50° и с попереч­ным уклоном до 20°. В первом случае необходимо лишь уст­ройство траншеи, а изоляция и укладка могут выполняться обычной колонной с несущественным изменением расстановки механизмов; второй случай требует совершенно новой техноло­гии устройства полок и т. д. Но если выделить по трассе уча­стки 4-го и 19-го типов, то на всех однотипных участках можно применять одинаковую технологию, что дает возможность оце­нивать выполняемые работы по заданному критерию оптималь­ности. Пусть в качестве критерия используются затраты на строительство работы w на единицу длины трубопровода. Для каждого типа местности можно применить несколько техноло­гических схем. Каждая из них требует определенных затрат w_{. Процесс поиска оптимальной последовательности работ будем рассматривать как многошаговый. На каждом шаге будем вво­дить в рассмотрение возможные технологические схемы и про­должать путь, имеющий наименьшую стоимость. Вследствие того что на каждом шаге продолжается лучший путь, на по следнем шаге будет достигнута наилучшая последовательность технологических схем в целом. Это условие можно записать в виде sy_onT = min(aUj + z/yi₊i), где w_t — минимальная стоимость работ на предыдущем пути; w_i+i — минимальная стоимость ра­бот на рассматриваемом шаге. Процесс реализации поиска оп­тимальной последовательности рассмотрим на участке трассы длиной L (см. рис. 10.2), включающей п участков l_i на каждом из которых

требуется смена технологии строительства по сравнению с предыдущим участком. Введем следующие обозначе­ния: Wi(l, 2,..., k) — затраты на строительство единицы длины трубопровода на местности i-ro типа по одной из k возможных технологических схем; гац — затраты на 1 км пути при переба­зировании строительных колонн (бригад) с участка 1-го типа на другой участок i-ro типа. Последний должен быть обяза­тельно однотипен с тем, на котором работала колонна, но не может быть его соседом. Поэтому колонна перебазируется на новый участок и сразу же приступает к работе по отлаженной на предыдущем участке технологии; Wi_m — затраты на переос­нащение колонны (бригады), работающей на участке i-ro типа по одной технологии, для работы на участке т-го типа по но­вой технологии; п — число колонн (бригад), работающих на строительстве участка L. Простейшим будет случай п=\, т. е. создана одна комплексная колонна, способная вести работы на местности любого типа в пределах L. Однако это не значит, что работа будет вестись от начала участка L до его конца после­довательно. В комплексной колонне в любом случае будут соз­даны специальные бригады для работ на разнотипных участках. Поэтому возникает задача использования основного звена комп­лексной механизированной колонны (одна бригада) и специа­лизированных бригад (две-три бригады и т. д.). Каким обра­зом использовать основное звено и специализированные бригады — это уже оптимизационная задача с п-м

числом бригад. Введем на первом шаге в рассмотрение стоимости ра­бот на первом участке W\ = w\ (1,2,3,4)/ь Цифры 1, 2, 3, 4 по­казывают, что на нем возможны четыре различные технологические схемы; соответственно будем иметь в виду и четыре стоимости. В качестве основной выбираем ту схему, стоимость которой минимальна, т. е. исследуем условие Wi = minwi(\, 2, 3,4)/,.

Переходим ко второму шагу. Бригада закончила работу на первом участке и подошла ко второму. Необходимо решить во­прос, переоснащать бригаду и приступать к работе на втором участке или переезжать на какой-либо участок с однотипной местностью и там продолжить работу. Из рис. 10.2,6 видно, что однотипны участки 1\, /₄ и /₇. Затраты на переоснащение колонны для работы на участке /₂ составляют w_l2, включая и убытки, которые могут быть из-за простоя лишней техники. Затраты на перебазировку с участка /_t на однотипный участок /₄ составят ^uCfe+'s); затраты на строительство на участке /₄ составят W₄ = mmw₄(l, 2...)/₄.

Таким образом, на втором шаге получим полную величину критерия оптимальности

'

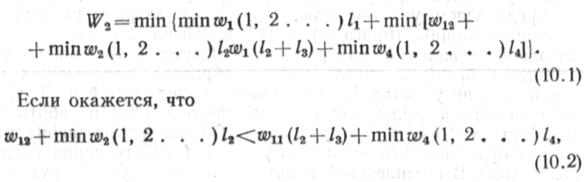
то необходимо переоснащение колонны и продолжение работ на участке /₂; в противном случае следует перебазироваться на участок /4. Однако это может не быть оптимальной последова­тельностью, если рассматривать весь участок L. Поэтому нужно продолжить процесс поиска оптимальной последовательности работ.

Переходим к участку /₃. Местность на нем отличается как от участка 1\, так и от участков /₂. Возможны два пути: колонна переоснащена для работы на участке /2, прошла его и, подойдя к участку /з, снова переоснащается для работы на нем; ра­бота на участке /2 ^не производится, а колонна перебазируется на однотипный участок /₄. Затраты на переоснащение колонны, закончившей работу на участке /₂, для работы на /₃ составят ЬУ₂з; затраты для выполнения работ на участке /₃ по аналогии с Л W₃ = mmw₃(\, 2...)/₃.

Можно поступить иначе: не переоснащая колонну для ра­боты на участке /з, перебазировать ее на однотипный участок /₂ через участок /е. Затраты на эту перебазировку и стоимость работ на участке /₆ составят Ш22('з + /4 + М +mina>₆(l, 2...)/_в.

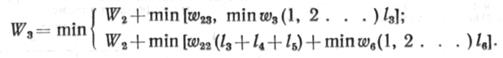
выражение должно быть проанализировано с учетом всех возможных путей продолжения технологической последователь­ности на втором шаге, определяемых формулой (10.1). Выше было отмечено, что, если имеет место условие (10.2), то ра­боты продолжаются на участке /₂ с переоснащением колонны, если нет, то — на участке 1₄. На третьем шаге должны быть исследованы возможности перехода с участка /а на /в. т. е. должны быть определены затраты из условия

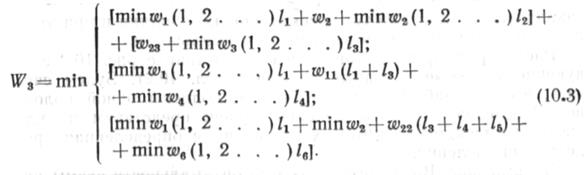
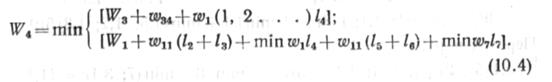
На четвертом шаге осуществляем переход с участка 1$ на участок /4 и проверяем целесообразность перехода на одно­типный участок /₄. По аналогии с предыдущим находим полную величину критерия оптимальности:

В этом выражении W₃ исследуется по всем вариантам, а не только по минимуму затрат.

Процесс поиска продолжаем аналогичным образом до тех пор, пока не появится необходимость возвращения колонны или бригады на предыдущие участки. Допустим, на каком-то шаге был достигнут последний участок, но остались незакон­ченными строительством какие-то предыдущие участки. Необ­ходимо вернуть колонну на один из этих участков и учесть зат­раты на возвращение. Допустим, что на четвертом шаге было установлено, что необходимо перебазировать колонну на уча­сток /4, а затем на /₇, т. е. при этом будут закончены строи­тельством все однотипные участки. Но работы на участках /2, /з, /s и /в будут еще не выполнены. Процесс оптимизации далее будем продолжать в обратном направлении, но исключив из рассмотрения уже законченные строительством участки /_ь /4, /₇. Процесс определения оптимальной последовательности заканчивается, когда будут рассмотрены все участки

и при этом получен минимум полной величины оптимальности.

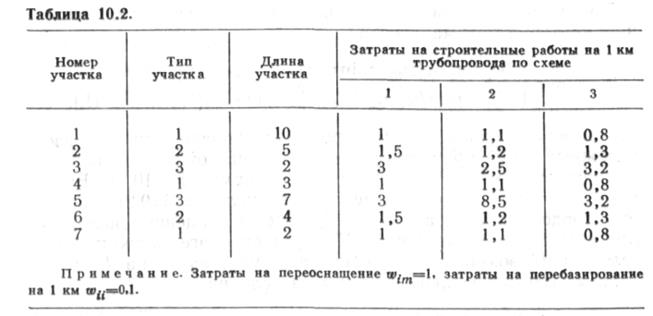
Рассмотрим пример, приняв в соответствии с рис. 10.2 сле­дующие условные исходные данные (табл. 10.2). Будем счи­тать, что все работы должны быть выполнены одной колон­ной. Последовательность решения задачи представим в виде шагов, на каждом из которых выполняется определенная про­цедура вычисления.

Первый шаг. Выбираем первые по оптимальности схемы ра­бот на каждом участке. Из табл. 10.2 для первого участка (тип местности 1) имеем W₍(3)=0,8.

Второй шаг. Определяем W₂ no формуле (10.1):

Как видно, на втором шаге более выгодными оказываются пе­ребазировка колонны и продолжение работы на участке /₄. Если принять вариант переоснащения колонны и продолжения работы на участке /₂, то стоимость работ будет W₂=15, на 3,9 условных единицы больше.

Третий шаг. Определяем W-, по формуле (10.3).

Используя данные табл. 10.2, получаем

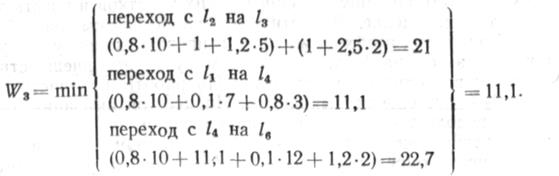
Подставив значения величин, входящих в W_b, получаем №5=18,2 (путь 1—4 — 7 — 6). Выполняя вычисления на по­следнем шаге, получаем следующие технологические последо­вательности (в возрастающем по затратам порядке): 49,2 (1 — 4 — 7 — 6 — 2 — 3 — 5); 49,7 (1 — 4 — 7 — 6—5 — 3—2); 50,6 (1—2 — 3 — 4 — 7 — 6 — 5); 51,3 (1, 2, 3, 4, 5, 6, 7 и 1, 2, 6, 7, 5, 4, 3); 51,7 (1, 2, 6, 7, 5, 3, 4); 52,6 (1, 2, 6, 5, 3, 4, 7); 54,3 (1, 2, 6, 5, 4, 3, 7). Схема последовательностей изображена на рис. 10.3. Как видно, в условиях рассматриваемого примера лучшей будет технологическая последовательность / — 4 — 7-6 — 2 — 3 — 5, в которой только два переоснащения колонны.

Date: 2015-06-07; view: 1047; Нарушение авторских прав