
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Учет упругого сопротивления
|
|
Рассмотренные перемещения при постоянной граничной силе определены в предположении, что сопротивление продольному перемещению формируется только за счет сил упругих и неупругих связей труб с грунтом. Это в идеальных условиях. Они могут иметь место только в двух случаях: конец трубы загружен и в трубопроводе имеются внутреннее давление и температурный перепад; к концу полубесконечного трубопровода приложена сосредоточенная сила. Во всех остальных случаях условно-граничное сечение труб испытывает сопротивление продольному перемещению, которое тем больше, чем выше продольная жесткость рассматриваемого участка.
Продольной жесткостью трубопровода (коэффициент упругого отпора) будем называть упругую характеристику, устанавливающую связь между перемещением конца полубесконечного трубопровода и самим перемещением:

где η (χ) — коэффициент продольной жесткости участка трубопровода в окрестностях рассматриваемого сечения χ; Ν, и — соответственно продольная сила и продольное перемещение в том же сечении.

|
Как видно из формулы (7.32), при и(х)~+0 η->-οο, при и(х)->оо η->-0. Примером продольной жесткости η->-οο может быть прямолинейный трубопровод условно-бесконечной длины при продольной силе меньше критической, т. е. вызывающей потерю устойчивости труб. В этом случае перемещение любого сечения труб теоретически равно нулю. Примером η-^οο является случай полубесконечного трубопровода со свободным концом, так как перемещение свободного конца труб ничем не ограничено. Промежуточные между предельными значениями продольной жесткости являются все другие значения η, определяемые в каждом конкретном состоянии. Например, линейная зависимость ΛΓ=η«0, нелинейная зависимость N = f(i\, u0n), где и0 — граничное перемещение; η — показатель степени. Сопротивление продольному перемещению конца полубесконечного трубопровода учитывается в граничной продольной силе, которая принимается в виде Р=(Р0— г\и0п). Так как th β /ι-И, формула (7.29) с учетом продольной жесткости будет иметь вид
при линейной зависимости для η; при нелинейной квадратичной зависимости
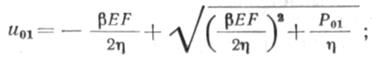
|
| При упругопластичных деформациях грунта и п= 1 выражение для продольного перемещения будет иметь вид |
при нелинейной степени зависимости
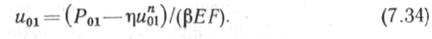
|
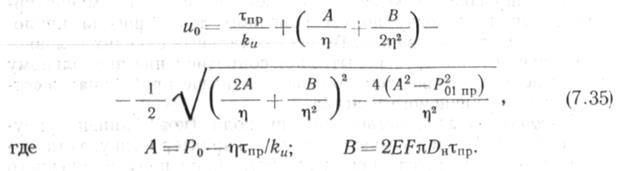
|
Влияние ползучести грунта на продольные перемещения трубопровода.
Рассмотренные выше перемещения трубопроводов условно можно назвать мгновенными, т. е. достигающими расчетного значения сразу же после приложения продольной силы. Перемещения трубопроводов в грунтах имеют, как правило, неустановившийся характер даже при постоянной сдвигающей нагрузке. Явление изменяющихся во времени деформаций грунта при постоянных напряжениях в механике грунтов называют ползучестью. Опыт показывает, что перемещения трубопровода при длительном воздействии нагрузки оказываются значительно большими, чем при воздействии мгновенных нагрузок. Это происходит вследствие проявления ползучих свойств грунта. В механике грунтов рассматривается ряд различных моделей ползучести. Каждая из них отличается принятием каких-либо допущений, условно описывающих характеристики ползучести. Поскольку нас интересует только ползучесть грунта при продольном перемещении, то опишем только те модели, которые могут быть использованы при расчете продольных перемощений.
Модель вязкого трения определяет касательные напряжения

где т]д — динамическая вязкость грунта; е — относительная деформация. Модель далека от описания реальных свойств ползучести, и использование ее в расчетах, хотя и дает простое решение, но приводит к большой погрешности, поскольку уравнение (7.36) описывает незатухающую ползучесть, имеющую постоянную скорость.
Модель Кельвина (применительно к продольным перемещениям)
| позволяет описать затухающую ползучесть следующим образом: |
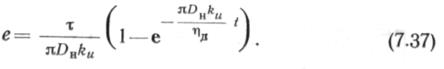
|
Как видно из уравнения (7.37), при t-^σο деформация достигает своего наибольшего значения и стабилизируется на величине e = r/nDHku.
Модель наследственной теории ползучести позволяет найти деформации ползучести от нагрузки, приложенной в момент времени с учетом касательных напряжений в грунте, существовавших до приложения данной нагрузки. Уравнение деформаций грунта с учетом ползучести имеет вид
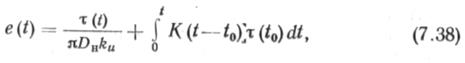
где K(t — to) —ядро ползучести, характеризующее скорость ползучести при постоянном напряжении в грунте.
Особенностью моделей (7.36) — (7.38) является то, что деформации грунта рассматриваются вне связи их с деформациями трубопровода, имеющими четко выраженный упругий характер. Поэтому предельные деформации труб при действии растягивающих усилий ограничивают и предельные деформации грунта, даже обладающего свойством ползучести. Как показали опыты, проводившиеся по ползучести грунтов при продольных перемещениях труб, наблюдаются два основных вида ползучести— затухающая и незатухающая.
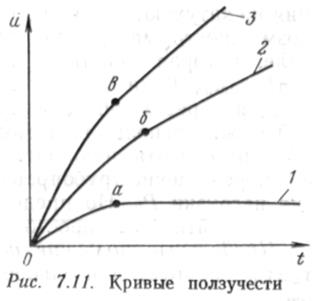
|
На рис. 7.11 изображены кривые ползучести при продольных перемещениях труб и. Кривая / характеризует затухающую ползучесть, при которой грунт «ползет» при постоянном сдвигающем усилии только в период времени 0—t 1 (участок кривой О— а). Кривые 2 и 3 иллюстрируют незатухающую ползучесть, т. е. грунт «ползет» при постоянном сдвигающем усилии неограниченное время. Естественно, что и деформация ползучести при этом может быть неограниченной. Отметим далее, что на участках 0— а, 0 — б, 0— в ползучесть неустановившаяся, т. е. имеет переменную скорость, а на участках далее точек а, б, в -установившаяся, т. е. грунт ползет с постоянной скоростью. Это очень важное обстоятельство, позволяющее при определении ползучих перемещений пользоваться простыми
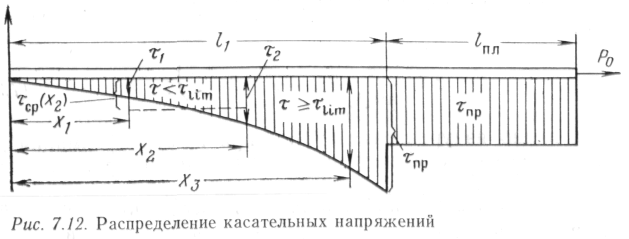
зависимостями. Одной из основных характеристик, определяемых в опытах по ползучести грунтов при продольном перемещении труб, является так называемый предел длительной прочности грунта. Под пределом длительной прочности понимают касательное напряжение по конкретной поверхности труба — грунт tlim, при котором ползучесть из затухающей переходит в незатухающую. Учитывая сказанное, рассмотрим, как происходит продольное перемещение прямолинейного полубесконечного трубопровода при длительном действии продольной силы. При этом будем иметь в виду, что ползучесть может проявляться как на участке упругой связи, так и на участке пластичной связи. Интересно, что на участке упругой связи предельная величина упругих продольных перемещений ограничена значением тпр/ku· Но особая форма переформирования частиц грунта в зоне контакта трубы с грунтом при длительном действии нагрузки позволяет, не изменяя картины напряженного состояния грунта в целом, перемещаться трубопроводу на значительно большие расстояния, чем определяемые условием т„р//г„. Этот факт интересен прежде всего тем, что продольное перемещение происходит при значениях τ, существенно меньших τπρ. На рис. 7.12 показан участок упругой 1\ и пластичной /„ связей. На участке х\ при t<ti (ti — касательные напряжения, при которых начинают проявляться ползучие перемещения) удлинения трубопровода за счет ползучести не будет; на участке х2 при ti<tnm ползучие перемещения будут затухающими. Наконец, на участке х3 при т^тцт ползучие перемещения не затухают до тех пор, пока полностью не будет исчерпана возможность материала труб к растяжению при продольной силе, которая действует в сечении х = 1{. Эта сила Р = Р0—
—яОпТпр/пл- ЕСЛИ /Пл = 0, ТО Р = Р0.
Для определения дополнительных, т. е. ползучих, перемещений можно использовать модели (7.36) —(7.38), которые позволяют рассчитать дополнительное (за счет ползучести) продольное перемещение трубопровода на любой момент времени действия нагрузки Ро. Но предельные дополнительные перемещения можно найти более просто.
Предельные ползучие перемещения. На участках /пл и Хз т^тмт, поэтому длительное действие силы Ρ при f-»-oo приве к полному использованию упругих свойств грунта. Конец трубопровода в сечении х = 1\ + 1„я переместится на величину
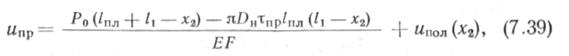
где и„ол — перемещения на участке х2, определяемые упругими и ползучими деформациями грунта.
Используя для описания ползучих свойств грунта зависимость (7.37) при ί-*-οο, получим
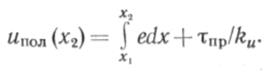
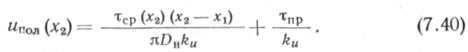
|
Если принять в пределах участка х2 среднее значение касательных напряжений τρρ(^2) (см. рис. 7.12), то перемещение
| Расстояния х\, х2 можно найти по формулам |
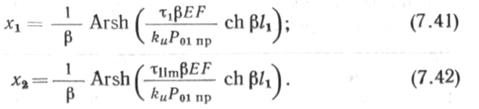
|
Можно использовать для определения «ПоЛ(*2) и уравнение перемещений с учетом ползучести, полученное нами на основании экспериментальных данных:
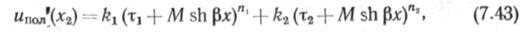
где k\, ki, n\, n-i — коэффициенты, определяемые опытным путем на коротких отрезках труб.
Нестабилизированные ползучие перемещения. Под нестабилизированными будем понимать перемещения, определяемые ползучестью грунта в момент времени />0. Для определения нестабилизированных перемещений на участке /пл можно использовать зависимость (7.36). Продольное перемещение конца участка /пл только за счет ползучести будет

Величина ипол(/пл) не может быть больше, чем позволяют упругие свойства материала труб, т. е.
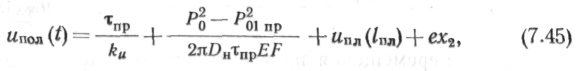
|
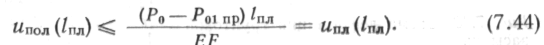
| Полное перемещение трубопровода в сечении л: = /1 + /пл складывается из перемещений участков /, и /пл, т. е. в момент времени / |
где перемещение ипл(1„л) определяется по формуле (7.44), а деформация е — по формуле (7.37). Наибольшее значение "пол (0 не может быть выше, чем ипр, определяемое по формуле (7.39).
В заключение необходимо отметить, что характеристики ползучести можно получить только опытным путем. Однако эти опыты требуют очень длительного времени. Поэтому при необходимости можно пользоваться формулой (7.45) с учетом (7.37), в которой вязкость т)д определяется довольно просто, например, по методу кольца и шара. Что касается предельных ползучих перемещений, то задача существенно упрощается введением условий, определяемых упругими свойствами трубопровода.
Расчетные характеристики грунтов. Примеры расчета продольных перемещений
|
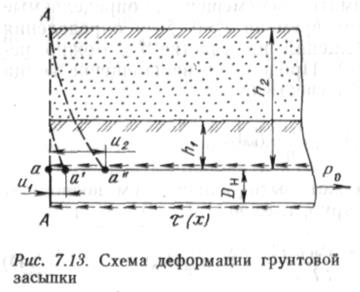
Расчетные характеристики грунтов. Для определения продольных перемещений трубопроводов необходимо иметь следующие физико-механические характеристики грунтов. Коэффициент постели грунта при сдвиге ku численно равен сдвигающему напряжению т, которое вызывает продольное перемещение единичной величины. Так, при &и = 1 Н/см3 перемещение в 1 см вызывает касательное напряжение т= 1 Н/см2. Обработка результатов многочислен-ных опытов показывает, что ku зависит от вида грунта, его состояния и толщины слоя грунта, окружающего трубу. Это обстоятельство можно пояснить с помощью рис. 7.13. К трубопроводу диаметром О„ прило-жена продольная сила Ро. Допустим, что материал труб нерастяжим; при этом по всей длине поверхности труб возникают одинаковые касательные напряжения т. До приложения нагрузки какая-то точка а находилась на вертикальной линии А — А. После приложения ро труба переместится вперед на величину и, которая будет зависеть от толщины слоя грунта h. Так, при ft = fti и = ыь а при Л = Й2 и = ич. При этом для совершенно

|
одинаковых грунтов Uz>u\, поскольку h2>h1. Учитывая линейный характер зависимости касательных напряжений и перемещений, можно использовать для определения ku следующую формулу:'


По формуле (7.46) можно найти ku для любого значения А2, имея при этом хотя бы одно значение ku для h\. Лучше всего его определить опытным путем. При отсутствии опытных данных можно использовать ориентировочные значения ku, полученные при толщине слоя грунта 1 м (табл. 7.1).
Предельные касательные напряжения тпр. Они зависят от вида, состояния грунта и средней глубины заложения труб в грунте. Сопротивление грунта сдвигу определяется по формуле Кулона тпр=о^ф + с, где а — нормальное напряжение; Ф — угол внутреннего трения грунта; с — сцепление грунта. Таким образом, от того, насколько правильно определено а, зависит и действительное тпр- Были проведены опыты с трубами диаметром от 300 до 1400 мм, которые четко показали, что можно принимать в расчетах ст=9«р=Уест h и соответственно
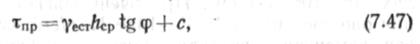
где уест — удельный вес грунта в естественном состоянии; Лср — средняя глубина заложения трубопровода (см. рис. 7.13).
Величина Лср не может быть больше, чем высота свода обрушения /ггв, определяемая по М. Протодьяконову, АСв = £//кр, где L = D» [1+2 tg (45°ф/2)]; fKp—коэффициент крепости грунта (табл. 7.2). Значения ф и с
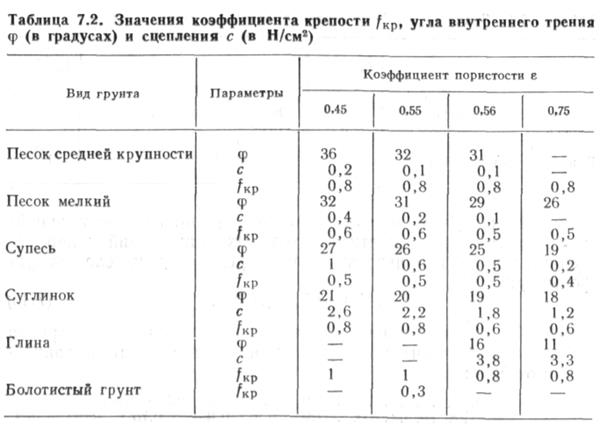
определяются испытанием грунта на сдвиг в сдвижном приборе (ГОСТ 12248—78). При отсутствии этих данных можно воспользоваться ориентировочными расчетными значениями ф и с, приведенными в табл. 7.2.
Характеристики ползучести. В зависимости от расчетной модели грунта необходимо иметь т]д в формулах (7.36) и (7.37) или так называемую меру ползучести К в уравнении (7.38). Если использовать уравнение (7.43), то необходимы данные о коэффициентах k\, k2, п\ и п2. Как уже отмечалось, все характеристики получают экспериментально. Эти эксперименты требуют весьма длительного времени проведения. Что касается динамической вязкости т)д, то она сравнительно просто определяется по известному методу кольца и шара или на сдвижном приборе. При определении т]д на сдвижном приборе коэффициент вязкости получают по формуле т)д = т/г/у, где т —замеренные в условиях опыта касательные напряжения; h — свободная высота образца, v — скорость смещения срезаемой части образца.
Опытами установлено, что значение т)д глинистых грунтов в тугопластичной и мягкой консистенциях колеблется в пределах 106—109 Н • с/см2. При очень мягкой и текучей консистенции оно составляет 10-10—10~12 Н-с/см2. Столь широкий диапазон изменения свидетельствует о необходимости определения характеристик ползучести для конкретных грунтов опытным путем.
Примеры расчета продольных перемещений. Во всех примерах примем следующие исходные данные: наружный диаметр труб £>я=122 см, толщина стенки труб 6=1,2 см, площадь сечения стенки трубы /7=455 см2, момент инерции / = 8,3- 105 см4, момент сопротивления W=l,36- 104 см3, площадь поперечного сечения трубы Ф=1,012-104 см2, модуль упругости металла Е= =21 • 10е Н/см2, сила тяжести единицы длины труб <7тр=35,8 Н/см, давление продукта в трубе р=50 МПа, начальная температура стенки труб 1„ — 0 "С.
Пример 1. (Основной расчетный случай).
Полубесконечный трубопровод, температура которого составляет в рассматриваемый момент времени?=30 °С, расположен в глинистом заторфованном грунте мягкой консистенции на средней глубине /!ср=150 см. Требуется найти продольное перемещение конца трубопровода и<>, находящегося под воздействием внутреннего давления р и температурного перепада А/= = t — to. Расчетная схема трубопровода показана на рис. 7.10. Продольное перемещение находим по формуле (7.31), предварительно определив недостающие составляющие этой формулы: тпр, Я0, An пр. Предельное касательное напряжение тпр находим по формуле (7.47); недостающие характеристики грунта Veer, «рис необходимо определить лабораторным путем. Примем ф и с, используя ориентировочные данные табл. 7.2: у<.ст=0,017 Н/см3, ф=11°, с=3,3 Н/см2. По формуле (7.47) тпр = 0,017 • 150- 0,2+3,3=3,8 Н/см2. Коэффициент постели грунта при сдвиге примем по табл. 7.2: ku = = 1,5 Н/см'. Граничное значение продольной силы найдем но формуле

где «I — коэффициент линейного расширения материала труб; для металла а(=1,2-Ю-5 1/°С. Подставляя в формулу (7.48) необходимые данные, получаем Р<н=500-1 -0,12-104+1,2 -Ю-5 -21 -10е -455 -30=8,49 -10е Н. Предельную силу poi пг найдем по формуле (7.30), где Р определяется по формуле (7.28)
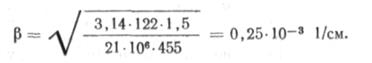
|
| Подставив значение р в (7.29), получим poi np = 6,05 • 10* Н. По формуле (7.31) искомое перемещение составит |

|
Таким образом, мгновенное перемещение конца полубесконечного трубопровода в рассмотренных условиях составит 3,81 см.
Пример 2. Определим ипр (условия см. в примере 1) с учетом ползучести грунта (в этом и последующих примерах цифровые расчеты не приводятся). Будем считать, что трубопровод должен работать время, достаточное для полного проявления ползучести. Это позволяет воспользоваться уравнением (7.39), в котором перемещение ипол(*2) находим по формуле (7.40).
В формуле (7.39) названа длина участка Хг- Найти ее можно, построив эпюру T=f(jc) и графически определив сечение хг, где т<Тцт можно получить аналитически по формуле (7.42).
В формуле (7.42) неизвестны тцт и 1\. Для определения Тнт можно воспользоваться следующим соотношением Тцт/Тпр:

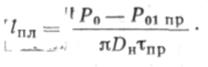
|
В рассматриваемом примере грунт — глина мягкопластичмая, Тцт^= = т„р -0,6 = 2,28 Н/см2. Что касается определения Л, то ее можно принять 3,5/р. Учитывая, что Р найдено в примере 1 и равно 0,25-10~3 1/см, находим fi = l,4-104 см. Подставляя далее в (7.42) необходимые значения величин, получаем дс2=1,18-10* см. По формуле (7.41), приняв Tt=0,6 Тцт, находим ДС| = 1,01-10* см. Далее, приняв тср=0,7 Тцга=1,6 Н/см2, находим по формуле (7.40) «Пол(*2) =7,26 см. В выражении (7.39) осталось неизвестным
Подставив в нее необходимые составляющие, получим /пл = 1,67-103 см. По формуле (7.39) находим предельное значение продольного перемещения

|
только /Пл. Его мы находим по формуле
конца трубопровода с учетом ползучести грунта unp = 10,14 см. Сравнив мгновенные перемещения и» (см. пример 1) и ыпр, видим, что учет ползучести грунта приводит к увеличению перемещения конца трубопровода в 2,66 раза. Следует отметить, что нарастание перемещений за счет ползучести происходит очень медленно. Это важно иметь в виду при проектировании и эксплуатации трубопроводов.
Пример 3. Определить продольное мгновенное перемещение конца полубесконечного трубопровода, испытывающего упругий отпор перемещению по линейному закону. Такой случай может иметь место, например, при повороте трубопровода в вертикальной или горизонтальной плоскости (рис. 7.14). Грунт препятствует продольному перемещению по закону r|Uo, и действительное значение растягивающей силы определяется как ЯД = Я0— 1\и<>, где tj — коэффициент упругого отпора перемещающемуся концу трубопровода. В рассматриваемом примере, приняв упругую модель грунта, коэффициент отпора Г) = *50Ф, где kit — коэффициент постели грунта при сжатии (табл. 7.3); Ф — площадь опирания конца трубопровода о грунт.
Пусть сечение х—1 расположено в свеженасыпанном песке с fe0 = 5 h/cms. Площадь опирания равна площади сечения трубы, т. е. Ф=1,012-104 см2. При этом т) = 5,06- 10* Н/см. Как и в предыдущих примерах, P0=8,49'10e H; Poinp = 6,05-10«Н; 0 = 0,25-10-» 1/см; т„р = 3,8 Н/см2; *„ = 1,5 Н/см3. Граничное перемещение «о находим по формуле (7.34), вычислил предварительно/1 и В по формуле (7.35): Л = 8,36-10«; В = 2,78-10". По формуле (7.34) и„=3,73 см.
Принятое в качестве упругого отпора сопротивление слабого свеженасыпанного песка по торцу трубы приводит к уменьшению перемещения по сравнению со свободным концом (пример 1) на 0,08 см. При более значительном отпоре например, за счет специального опорного устройства, разница будет большей.
Пример 4. Определить перемещение трубопровода I, соединенного с трубопроводом 2 (рис. 7.14, б) и расположенного в песчаном грунте.

|
Перемещение и0 находим по формуле (7.34), как и в предыдущем примере. Значение упругого отпора перемещения найдем, рассматривая трубопровод 2 как балку в упругой грунтовой среде:
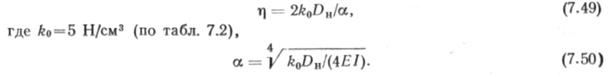
Подставив в (7.50) значение величин, находим a=l,72-10~3 1/см. По формуле (7.49) г)=7,09-105 Н/см, т. с. в 14 раз больше, чем в предыдущем случае.
Прежде чем определить по формуле (7.34) ц0, нужно по формуле (7.33) найти Uo и сравнить его с иПр=ТпР/£„. Если окажется, что uoi<"np, то расчет по формуле (7.34) не требуется, так как участок /пл не образуется. При "oi>unp его необходимо определить по формуле (7.33). Выполняя вычисления, находим

По формуле (7.29) и0щр = 2,53 см. Поэтому граничное перемещение следует определять по формуле (7.34). Выполнив вычисления, получим и0=2,75 см.
Сравнив мгновенные перемещения в примерах 1, 3 и 4, имеем и0 = = 3,81 см (свободный конец трубы), и0=3,73 см (т) = 5,06-104 Н/см), Uo-= =2,75 см (ti = 7,09 • 105 Н/см). Эти данные наглядно иллюстрируют важность учета упругого отпора. Наконец, пример 2 показывает исключительное значение учета ползучести грунта.
Возвращаясь к примеру 4, определим силу, с которой трубопровод 1 действует на трубопровод 2:
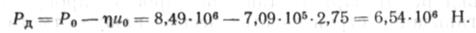
Упругий изгиб трубы 2 уменьшает действие продольной силы со стороны трубы /.
Раздел IV
Date: 2015-06-07; view: 1583; Нарушение авторских прав