Формализация процесса расстановки НС

Графический метод расстановки НС чрезвычайно осложняет получение наилучшего решения задачи о выборе оптимальной трассы. Для использования методов оптимального проектиро­вания при выборе наилучшей трассы необходимо формализо­вать рассмотренный метод таким образом, чтобы НС можно было расстанавливать без графических построений П. П. Бородавкиным и Б. И. Кимом предложен следующий алгоритм оп­ределения числа и расстановки НС, легко реализуемый на ЭВМ. Запишем формулу (2.36) в виде

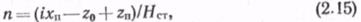
где х_n — координата перевальной точки; z₀, z_n — отметка на­чальной и перевальной точек; H_ст — напор на выходе из НС.

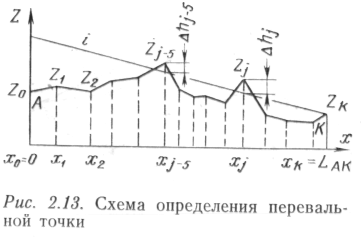
Неизвестными величинами в (2.15) являются хn и z_n, для определения которых необходимо исследовать профиль трассы нефтепровода на наличие перевальной точки. Рассмотрим произ­вольный профиль трассы длиной /, заданный координатами то­чек излома рельефа местности (рис. 2.13). Проведем из конце­вой точки трубопровода (x_k, z_k) заданную линию гидравличе­ского уклона. Если на профиле имеются перевальные точки, то линия гидравлического уклона пересечет или коснется про­филя трассы.

Из рисунка видно, что возможное превышение каких-либо

точек профиля над линией

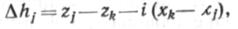
где j = 1, 2, 3,..., k.

Рассмотрим следующие случаи: Ah_j,<0; Ah_jj>0; Ah_j<=0.

В первом случае пере­вальная точка на профиле отсутствует. Отсюда z_n = z_k и х_n = l_АК. Во втором слу­чае перевальная точка на­ходится среди некоторого числа точек с Ah_j>0. Точка с максимальным значением Ah_j и будет перевальной,

а ее координаты искомыми величинами. В третьем случае пе­ревальной будет точка с Ah_j= 0 и с минимальным для данного i значением X_j.

Алгоритм решения задачи определения числа НС при про­филе трассы, заданном набором значений

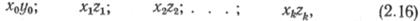
и гидравлическом уклоне i можно описать следующим образом.

Первый шаг. Исключаем из (2.16) все точки с z<=z_k.

Второй шаг. Для х=х_k-1 (если эта точка 'не исключена) определяем Ah_k-1. Если Ah_k-1, то значения X_k-1, z_k-1 и Ah_k-1 заносим в специальный список (назовем его со) и исклю­чаем из (2.16) точки с с z<=z_k. Если Ah_k-1<0, то исключаем эту точку, а заодно и все точки z<=z из (2.16) и из дальней­шего рассмотрения. Далее для x = X_k-2 (если эта точка уже ис­ключена, то рассматриваем x=x_k-3-) определяем Ah_k-2. Анало­гично, если Ah_k-2>0, значения х_k-2, z _k-2 и Ah_k-2 заносим в спи­сок со и исключаем из (2.16) точки с z<=z_k-2. Если Ah_k-2<0, то исключаем эту точку, а вместе с ней и все точки z<=z_k-2 из даль­нейшего рассмотрения. Вычисления выполняем последовательно для всех x ₀<х<х_k.

Третий шаг. Рассматриваем список со. Если в нем не оказа­лось ни одного значения Ah_j, то х_п = l_АК и z_Л = z_k. В противном случае (если в списке со имеются точки с Ah_j>=0) определяем max Ah_j и min x_j, если Ah_j = 0.

Четвертый шаг. Определяем по (2.15) число НС n.

Уравнение линий гидравлического уклона для определения координат любой НС можно представить в виде

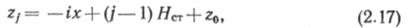
где j — порядковый номер НС; х — текущая координата.

Точки пересечения с профилем трассы и будут искомыми ко­ординатами (координаты первой станции х = х_o, z=z_o).

Число НС (n), определяемое по формуле (2.15), оказыва­ется чаще всего дробным и округляется до ближайшего целого. При округлении числа НС в большую сторону (допустим, до n') необходимо уменьшить напор, приходящийся на каждую станцию, до H'_ст = (n/n')H_ст.

Координаты НС получим, определив точки пересечения линии (2.17) с профилем трассы при H_ст и n'>=j>1.

Рассмотрим случай, когда число НС округлено в меньшую сторону, предположим, до n*. Уменьшение числа НС обычно компенсируют прокладкой лупинга, длина которого Л*. Стои­мость сооружения лупинга, как и основной нитки, зависит от условий местности. Поэтому целесообразно разместить его по трассе так, чтобы стоимость строительства была наименьшей. Вычислим координаты НС по формуле (2.17) при всех n*>=j>1 и обозначим их через x_j, z_j. Прокладка лупинга позволяет изме­нить положение промежуточных НС в некоторых пределах. Для определения границ возможного расположения НС воспользу­емся уравнением.

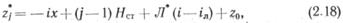
соответствующим размещению лупинга на любом перегоне между НС (здесь i_Л — гидравлический уклон лупинга).

Обозначим точки пересечения линии (2.18) с профилем трассы через х_j*, z_j*. Исследуем далее условия местности на участке прокладки лупинга длиной Л* перед точками x₂*, z₂*, x_з*, z₃*,..., x_n*, z_n* и х_n, z_n. Поскольку величина i _Л<1, то на некоторых участках перед НС может оказаться локальная пе­ревальная точка. В этих случаях для определения стоимости сооружения лупинга необходимо рассматривать участок мест­ности длиной X_jn — х_j, где х_j'— решение уравнения (2.18) и уравнения линий гидравлического уклона, проходящей через локальную перевальную точку (обозначим ее х_jn, z_jn):

Если для прокладки лупинга выбран участок перед концевой или перевальной точкой трубопровода, то окончательными ко­ординатами НС будут х_j, Zj, а если этот участок выбран перед второй НС, то ее координатами будут х_j*, z _j*. В остальных случаях координаты НС определяются соответствующими рас­четами.

Алгоритм решения задачи расстановки НС при заданном профиле трассы (2.16) и гидравлических уклонах в магистрали и лупинге описывается следующим образом.

Первый шаг. Определяем координаты второй НС по формуле (2.17) при j = 2. Для этого вычисляем z_2,1 при х = х₁ и сравни­ваем с г\. Если z_2,1<Z₁, то, интерполируя z₂ в интервале xb<x<.xi, находим х₂ и z₂. Если 22,1=21, то вычисляем z₂,₂ при х=х₂ и сравниваем с z₂. Если z_2,2<z₂, то х₂ = х₁ и z₂=z₁. Если z_2,2>z₁ то вычисляем z₂,^ при х=х₃ и сравниваем с zз, и т. д. Если z_2,1>z₁, то вычисляем z_2,2 и сравниваем с z₂. Про­должаем таким образом вычисления для всех х_о<х<х_n до тех пор, пока не найдем х₂ и z₂. Затем при j = 3 и x ₂<х<х_n опре­деляем х₃ и z₃, и т. д.

Второй шаг. Аналогичным образом вычисляем х_j*, z_j* по формуле (2.18).

Третий шаг. Исследуем по исходной информации условия местности на участке длиной Л* перед точками х₂*, z₂*; x _з*, z₃*; х*_п*,, z*_n*, х_п, z_n. Вычисляем стоимости прокладки лупинга на каждом из этих участков и выбираем наилучший, т. е. тот, которому соответствуют наименьшие затраты.

Координатами насосных станций, находящихся до лупинга, будут x₁, z₁; x₂, z₂; x_i*-1, z_j*-1, а для станций, расположенных

после лупинга, x_j^*,z_j*,....,x_n**, z_n**, где j* — номер НС, перед

которой размещен лупинг.

При целом числе станций или округлении п в большую сто­рону решение заканчивается первым шагом.

Date: 2015-06-07; view: 864; Нарушение авторских прав