
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод зон Френеля
|
|
За допомогою принципу Гюйгенса–Френеля можна обґрунтувати з хвильових властивостей світла закон прямолінійного поширення світла в однорідному середовищі. Френель розв’язав цю задачу, розглянувши взаємну інтерференцію вторинних хвиль, і застосував прийом, який отримав назву методу зон Френеля.
Знайдемо в довільній точці М амплітуду світлової хвилі, що поширюється в однорідному середовищі від точкового джерела 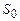 .
.
Згідно з принципом Гюйгенса–Френеля замінимо дію джерела 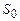 дією уявних джерел, які розміщені на допоміжній поверхні S, що є однією з хвильових поверхонь хвилі, яка поширюється від джерела
дією уявних джерел, які розміщені на допоміжній поверхні S, що є однією з хвильових поверхонь хвилі, яка поширюється від джерела 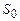 (рис. 2.9).
(рис. 2.9).
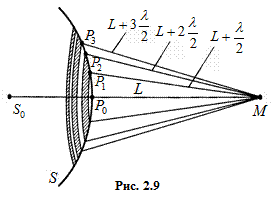
Ця допоміжна поверхня є поверхнею сфери з центром в 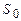 . Френель розбив хвильову поверхню S на кільцеві зони такого розміру, щоб відстані від країв зони до М відрізнялись на
. Френель розбив хвильову поверхню S на кільцеві зони такого розміру, щоб відстані від країв зони до М відрізнялись на 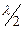 (
(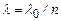 , де
, де 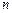 – показник заломлення середовища), тобто
– показник заломлення середовища), тобто
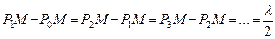 .
.
Подібне розбивання хвильової поверхні S на зони можна виконати, провівши з точки М концентричні сфери радіусами
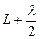 ;
; 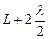 ;
; 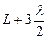 ;...
;...  .
.
Точки сфери S, що лежать від точки М на відстанях 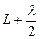 ;
; 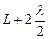 ;
; 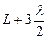 і т.д. утворюють межі 1-ї, 2-ї, 3-ї і т.д. зон Френеля.
і т.д. утворюють межі 1-ї, 2-ї, 3-ї і т.д. зон Френеля.
Оскільки коливання від сусідніх зон проходять до точки М відстані, які відрізняються на 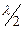 , то в точку М вони надходять з протилежними фазами і при накладанні ці коливання будуть взаємно ослаблюватися. Тому амплітуда результуючого коливання в точці М
, то в точку М вони надходять з протилежними фазами і при накладанні ці коливання будуть взаємно ослаблюватися. Тому амплітуда результуючого коливання в точці М
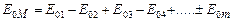 , (2.24)
, (2.24)
де 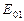 ,
, 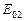 , …
, … 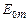 – амплітуди коливань, що збуджуються 1-ю, 2-ю,…, m -ю зонами. В цей вираз всі амплітуди коливань від непарних зон входять зі знаком „+”, а від парних зон – зі знаком „–”.
– амплітуди коливань, що збуджуються 1-ю, 2-ю,…, m -ю зонами. В цей вираз всі амплітуди коливань від непарних зон входять зі знаком „+”, а від парних зон – зі знаком „–”.
Величина 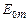 залежить від площі
залежить від площі 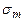 m -ї зони і кута
m -ї зони і кута 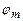 між зовнішньою нормаллю до поверхні зони в якій-небудь її точці і прямою, яка напрямлена з цієї точки в точку М.
між зовнішньою нормаллю до поверхні зони в якій-небудь її точці і прямою, яка напрямлена з цієї точки в точку М.
Із збільшенням номера зони m зростають кут 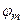 і відстань від зони до точки М. Згідно із принципом Гюйгенса-Френеля це приводить до монотонного зменшення інтенсивності випромінювання в напрямку точки M. Тому
і відстань від зони до точки М. Згідно із принципом Гюйгенса-Френеля це приводить до монотонного зменшення інтенсивності випромінювання в напрямку точки M. Тому
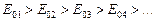 .
.
Загальне число N зон Френеля, які вміщуються на частині сфери, яка повернена до точки М, дуже велике. Тому можна вважати, що в межах не дуже великих змін m залежність 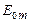 від m є лінійною, і амплітуда коливань, яка викликана якою-небудь m -ю зоною, дорівнює півсумі амплітуд коливань, що викликані
від m є лінійною, і амплітуда коливань, яка викликана якою-небудь m -ю зоною, дорівнює півсумі амплітуд коливань, що викликані  -ю і
-ю і 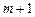 -ю зонами. Тобто
-ю зонами. Тобто
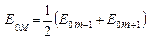 . (2.25)
. (2.25)
Тоді амплітуда результуючого коливання в точці М матиме такий вигляд:
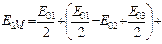
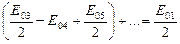 , (2.26)
, (2.26)
оскільки усі вирази, що стоять у дужках, дорівнюють нулю. Тоді амплітуда коливань, що створюється в довільній точці М сферичною хвильовою поверхнею, дорівнює половині амплітуди коливань, що створюється однією центральною зоною. Дія всієї хвильової поверхні на точку М зводиться до дії її малої ділянки, меншої, ніж центральна зона.
Отже, поширення світла від джерела світла 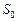 до точки М відбувається так, немовби світловий потік поширюється всередині дуже вузького каналу вздовж
до точки М відбувається так, немовби світловий потік поширюється всередині дуже вузького каналу вздовж 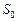 M, тобто прямолінійно. У такий спосіб хвильовий принцип Гюйгенса-Френеля дозволяє пояснити прямолінійне поширення світла в однорідному середовищі.
M, тобто прямолінійно. У такий спосіб хвильовий принцип Гюйгенса-Френеля дозволяє пояснити прямолінійне поширення світла в однорідному середовищі.
Інтенсивність світла в точці M можна значно збільшити, якщо закрити всі парні або непарні зони Френеля. Тоді результуюча амплітуда коливань відповідно дорівнюватиме:
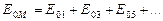
або
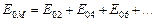 .
.
Екран, який перекриває всі парні або непарні зони Френеля, називається зонною пластинкою. Пластинка має складатися з прозорих або непрозорих кілець, радіуси яких дорівнюють 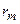 . Радіуси прозорих кілець підраховують для m= 0, 2, 4 ,…, непрозорих – для m= 1, 3, 5,….
. Радіуси прозорих кілець підраховують для m= 0, 2, 4 ,…, непрозорих – для m= 1, 3, 5,….
§2.2.3. Дифракція Фраунгофера на одній щілині
Дифракція Фраунгофера – це дифракція плоских світлових хвиль, коли джерело світла і точка спостереження нескінченно віддалені від перешкоди, яку огинають хвилі. Для здійснення дифракції Фраунгофера потрібно джерело світла 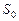 помістити у фокусі збиральної лінзи
помістити у фокусі збиральної лінзи 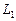 , а дифракційну картину досліджувати у фокальній площині другої збиральної лінзи
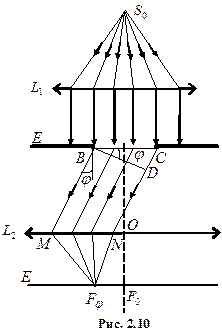
, а дифракційну картину досліджувати у фокальній площині другої збиральної лінзи 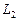 , встановленої за перешкодою (рис. 2.10).
, встановленої за перешкодою (рис. 2.10).
Нехай паралельний пучок монохроматичного світла падає нормально на непрозору плоску поверхню, в якій прорізано вузьку щілину ВС, що має сталу ширину а=ВС і довжину l>>а (рис. 2.10). Згідно принципу Гюйгенса-Френеля точки щілини є вторинними джерелами хвиль, які коливаються в однакових фазах, бо площина щілини збігається з фронтом падаючої хвилі.
У побічному фокусі 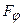 лінзи
лінзи 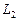 збираються всі паралельні промені, які падають на лінзу під кутом
збираються всі паралельні промені, які падають на лінзу під кутом 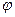 до її головної оптичної осі
до її головної оптичної осі 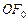 , що перпендикулярна до фронту падаючої хвилі. При цьому оптична різниця ходу
, що перпендикулярна до фронту падаючої хвилі. При цьому оптична різниця ходу 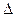 між крайніми променями CN і BM дорівнює
між крайніми променями CN і BM дорівнює 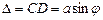 . ВD – перпендикуляр, який опущений з точки В на промінь CN.
. ВD – перпендикуляр, який опущений з точки В на промінь CN.
 Результат інтерференції світла в точці
Результат інтерференції світла в точці 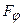 визначиться числом зон Френеля, що вкладається в щілині. Якщо кількість зон парна, то
визначиться числом зон Френеля, що вкладається в щілині. Якщо кількість зон парна, то
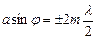 ,
, 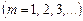 (2.27)
(2.27)
і в точці 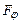 буде дифракційний мінімум
буде дифракційний мінімум 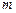 – го порядку. Знак “–” у правій частині рівності (2.27) відповідає променям світла, які поширюються від щілини під кутом –
– го порядку. Знак “–” у правій частині рівності (2.27) відповідає променям світла, які поширюються від щілини під кутом – 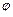 і збираються в побічному фокусі
і збираються в побічному фокусі 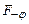 лінзи, який симетричний до
лінзи, який симетричний до 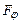 відносно головного фокусу
відносно головного фокусу 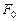 . Якщо кількість зон непарна, то
. Якщо кількість зон непарна, то
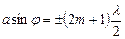 ,
, 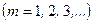 , (2.28)
, (2.28)
і в точці 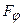 буде дифракційний максимум
буде дифракційний максимум 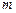 – го порядку з інтенсивністю
– го порядку з інтенсивністю 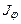 і який відповідає дії однієї зони Френеля.
і який відповідає дії однієї зони Френеля.
У напрямку j= 0 спостерігатиметься найінтенсивніший центральний максимум нульового порядку інтенсивністю 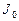 .
.
Залежність відношення 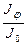 від
від 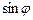 наведено на рис. 2.11.
наведено на рис. 2.11.
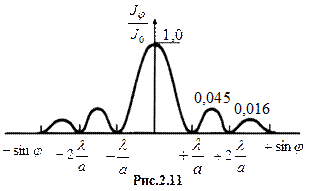
Розрахунок показує, що інтенсивності центрального і наступних максимумів співвідносяться як
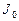 :
: 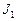 :
: 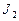 :
: 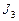 = 1:0,045:0,016:0,0083:…,
= 1:0,045:0,016:0,0083:…,
тобто основна частина світлової енергії зосереджена в центральному максимумі.
§2.2.4. Дифракція Фрунгофера на двох щілинах
Розглянемо дифракцію плоскої монохроматичної хвилі, яка падає нормально на поверхню, що містить дві щілини. Позначимо BC=DP=a; CD=b; d=a+b (рис. 2.12). Коливання в усіх точках щілин відбуваються в одній фазі, оскільки ці точки лежать на тій самій хвильовій поверхні. Знайдемо результуючу амплітуду коливань у точці 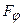 екрана Е, в якій збираються промені від двох щілин, що падають на лінзу L під кутом j до її оптичної осі
екрана Е, в якій збираються промені від двох щілин, що падають на лінзу L під кутом j до її оптичної осі 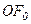 .
.
Очевидно, що в тих напрямках, в яких одна із щілин не поширює світла, воно не буде поширюватися і при двох щілинах, тобто головні мінімуми інтенсивності будуть спостерігатися в напрямках, що визначаються умовою:
a sin j= 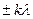 , (k= 1, 2, 3 ,…). (2.29)
, (k= 1, 2, 3 ,…). (2.29)
Різниця ходу променів, що йдуть від двох сусідніх щілин становить
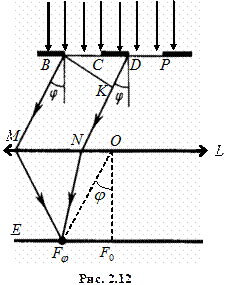
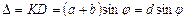 . (2.30)
. (2.30)
Внаслідок взаємної інтерференції світлових променів, які посилаються двома щілинами, в деяких напрямках промені будуть гасити один одного, тобто виникнуть додаткові мінімуми. Ці додаткові мінімуми будуть спостерігатися для променів, які поширюються від точок B і D двох щілин, якщо різниця ходу променів 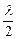 ,
, 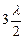 , ….
, ….
Отже, з урахуванням 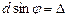 умовадодаткових мінімумів:
умовадодаткових мінімумів:
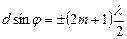 ,
, 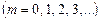 . (2.31)
. (2.31)
Якщо ж в різниці ходу променів, які випромінюються з точок B і D, вміщується ціле число довжин хвиль, а саме 0, 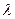 ,
, 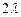 ,..., то дія одної щілини буде підсилюватися дією іншої. Отже, умова головних максимумів
,..., то дія одної щілини буде підсилюватися дією іншої. Отже, умова головних максимумів
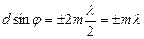 ,
, 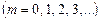 . (2.32)
. (2.32)
§2.2.5. Дифракція світла на дифракційній гратці
Розглянемо дифракцію світла, зумовлену дією дифракційної гратки.
Дифракційна гратка – це система з великої кількості N однакових за шириною щілин і паралельних одна до одної, які лежать в одній площині і відокремлені непрозорими проміжками, однаковими за шириною. Для пояснення дифракцію світла, зумовлену дією дифракційної гратки використаємо рис. 2.12. На рис. 2.12 також BC=DP=a; CD=b; d=a+b – період дифракційної гратки.
Якщо монохроматична хвиля падає нормально на поверхню гратки, то коливання в усіх точках щілин відбуваються в однаковій фазі, оскільки ці точки лежать на одній хвильовій поверхні.
Запишемо результуючу амплітуду коливань у точці 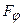 екрана Е, в якій збираються промені від усіх щілин гратки, що падають на лінзу L під кутом j до її головної оптичної осі
екрана Е, в якій збираються промені від усіх щілин гратки, що падають на лінзу L під кутом j до її головної оптичної осі 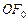 . Якщо дифракційна гратка складається з N щілин, то умовою головних максимумів є вираз
. Якщо дифракційна гратка складається з N щілин, то умовою головних максимумів є вираз
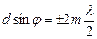 ,
, 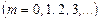 , (2.33)
, (2.33)
а умовою головних мінімумів − вираз
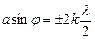 ,
, 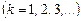 . (2.34)
. (2.34)
Умова додаткових мінімумів –
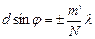 , (2.35)
, (2.35)
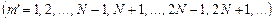
або
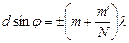 ,
, 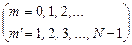 . (2.36)
. (2.36)
Між двома сусідніми додатковими мінімумами утворяться максимуми, які називаються вторинними.
Між двома сусідніми головними максимумами знаходиться N –1 додаткових мінімумів і N– 2 вторинних максимумів. На них накладатимуться мінімуми, що виникають при дифракції від однієї щілини.
Із формул
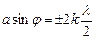 і
і 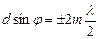
видно, що головний максимум m- го порядку збігається з k- им мінімумом від одної щілини, якщо виконується рівність
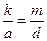 , або
, або 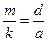 .
.
На рис. 2.13 наведено розподіл інтенсивності 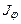 світла в дифракційній картині від sin φ для
світла в дифракційній картині від sin φ для 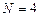 і
і 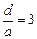 .
.
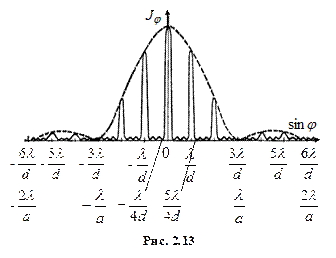
Пунктирна крива, що проходить через вершини головних максимумів, зображає інтенсивність, яка зумовлена дифракцією на одній щілині. Як видно з рис. 2.13, при відношенні 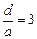 головні максимуми 3 - го, 6 - го тощо порядків збігаються з мінімумами інтенсивності від однієї щілини, тому ці максимуми зникають.
головні максимуми 3 - го, 6 - го тощо порядків збігаються з мінімумами інтенсивності від однієї щілини, тому ці максимуми зникають.
Якщо дифракційну гратку освітлюють білим світлом, то для різних значень 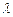 положення всіх головних максимумів, крім центрального, не збігаються один з одним. Тому центральний максимум має вигляд білої смужки, а всі інші – кольорових смужок, які називають дифракційними спектрами першого, другого і вищих порядків. У межах кожної смужки забарвлення змінюється від фіолетового біля внутрішнього краю, який найближчий до максимуму нульового порядку до червоного – біля зовнішнього краю дифракційної картини. Таким чином, дифракційна гратка розкладає немонохроматичне світло в дифракційний спектр і її можна використовувати як дисперсійний прилад.
положення всіх головних максимумів, крім центрального, не збігаються один з одним. Тому центральний максимум має вигляд білої смужки, а всі інші – кольорових смужок, які називають дифракційними спектрами першого, другого і вищих порядків. У межах кожної смужки забарвлення змінюється від фіолетового біля внутрішнього краю, який найближчий до максимуму нульового порядку до червоного – біля зовнішнього краю дифракційної картини. Таким чином, дифракційна гратка розкладає немонохроматичне світло в дифракційний спектр і її можна використовувати як дисперсійний прилад.
§2.3. Поляризація світла
§2.3.1. Природне і поляризоване світло. Закон Малюса
Наслідком теорії Максвелла є твердження про поперечність світлових хвиль: вектори напруженості електричного 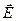 і магнітного
і магнітного 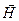 полів електромагнітної хвилі взаємно перпендикулярні і коливаються перпендикулярно до вектора швидкості
полів електромагнітної хвилі взаємно перпендикулярні і коливаються перпендикулярно до вектора швидкості 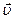 поширення хвилі. При розгляді світлових електромагнітних хвиль усі міркування зазвичай проводять для вектора
поширення хвилі. При розгляді світлових електромагнітних хвиль усі міркування зазвичай проводять для вектора 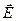 , який називається світловим вектором, тому що він має визначальний вплив при дії світла на речовину. Площина, в якій відбувається коливання вектора
, який називається світловим вектором, тому що він має визначальний вплив при дії світла на речовину. Площина, в якій відбувається коливання вектора 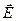 , називається площиною поляризації, а перпендикулярна до неї площина – площиною коливань.
, називається площиною поляризації, а перпендикулярна до неї площина – площиною коливань.
Світло є сумарним електромагнітним випромінюванням множини атомів. Атоми випромінюють світлові хвилі незалежно один від одного у вигляді хвильового цугу, в якому вектор 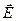 коливається в одній площині. Хвильові цуги неперервно накладаючись змінюють один одного. Тому світлова хвиля, що випромінюється тілом, характеризується рівноймовірними напрямками коливань світлового вектора
коливається в одній площині. Хвильові цуги неперервно накладаючись змінюють один одного. Тому світлова хвиля, що випромінюється тілом, характеризується рівноймовірними напрямками коливань світлового вектора 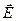 .
.
Природним (неполяризованим) називається світло з усіма можливими рівноймовірними орієнтаціями вектора 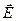 (отже, і
(отже, і 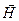 ) (рис. 2.14, а).
) (рис. 2.14, а).
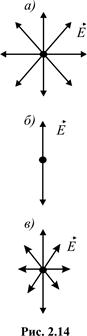 Поляризованим називається світло, в якому напрямки коливань вектора
Поляризованим називається світло, в якому напрямки коливань вектора 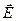 певним чином упорядковані.
певним чином упорядковані.
Якщо коливання вектора 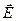 світлової хвилі відбуваються в одній певній площині, то світло називається лінійно поляризованим (плоскополяризованим (рис. 2.14, б). У випадку, коли вектор
світлової хвилі відбуваються в одній певній площині, то світло називається лінійно поляризованим (плоскополяризованим (рис. 2.14, б). У випадку, коли вектор 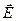 описує еліпс в площині перпендикулярній до напрямку поширення променя, то така хвиля називається еліптично поляризованою, а якщо коло - поляризованою по колу (циркулярно поляризованою).
описує еліпс в площині перпендикулярній до напрямку поширення променя, то така хвиля називається еліптично поляризованою, а якщо коло - поляризованою по колу (циркулярно поляризованою).
Коли вектор 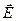 обертається проти годинникової стрілки в площині перпендикулярній до напрямку поширення променя, то поляризація називається правою, а в протилежному випадку – лівою.
обертається проти годинникової стрілки в площині перпендикулярній до напрямку поширення променя, то поляризація називається правою, а в протилежному випадку – лівою.
Якщо внаслідок яких-небудь зовнішніх впливів має місце переважаючий напрямок коливань вектора 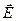 , то світло є частково поляризованим (рис. 2.14, в).
, то світло є частково поляризованим (рис. 2.14, в).
Для характеристики поляризаційного стану використовують величину, яку називають ступінню поляризації:
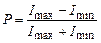 , (2.37)
, (2.37)
де 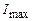 і
і 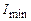 – відповідно, максимальна і мінімальна інтенсивність світла, що відповідають двом перпендикулярним компонентам вектора
– відповідно, максимальна і мінімальна інтенсивність світла, що відповідають двом перпендикулярним компонентам вектора 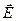 . Для природного світла
. Для природного світла 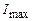 =
= 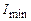 і Р= 0. Для плоскополяризованого –
і Р= 0. Для плоскополяризованого – 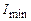 = 0 і Р= 1.
= 0 і Р= 1.
Поляризацією світла називається виділення лінійно поляризованого світла з природного або частково поляризованого.
 Плоскополяризоване світло можна отримати з природного за допомогою приладів, які називаються поляризаторами. Ці прилади вільно пропускають коливання, паралельні до площини поляризації, яка називається головною площиною, і повністю або частково затримують коливання, які перпендикулярні цій площині. В ролі поляризаторів можуть бути середовища, які анізотропні відносно коливань вектора
Плоскополяризоване світло можна отримати з природного за допомогою приладів, які називаються поляризаторами. Ці прилади вільно пропускають коливання, паралельні до площини поляризації, яка називається головною площиною, і повністю або частково затримують коливання, які перпендикулярні цій площині. В ролі поляризаторів можуть бути середовища, які анізотропні відносно коливань вектора 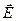 , наприклад, кристали. Одним із природних кристалів, які використовуються як поляризатори, є турмалін. Прилади, за допомогою яких аналізують ступінь поляризації світла, називають аналізаторами.
, наприклад, кристали. Одним із природних кристалів, які використовуються як поляризатори, є турмалін. Прилади, за допомогою яких аналізують ступінь поляризації світла, називають аналізаторами.
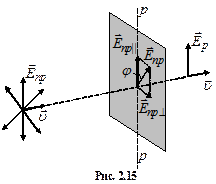
Якщо на поляризатор падає природне світло (рис. 2.15), то при вході в поляризатор падаючу хвилю, вектор напруженості 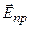 електричного поля якої коливається у площині, що утворює з головною площиною поляризатора р–р кут
електричного поля якої коливається у площині, що утворює з головною площиною поляризатора р–р кут 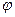 , можна зобразити у вигляді двох коливань у взаємно перпендикулярних площинах (рис. 2.15). Причому амплітуди коливань можна виразити таким чином:
, можна зобразити у вигляді двох коливань у взаємно перпендикулярних площинах (рис. 2.15). Причому амплітуди коливань можна виразити таким чином:
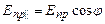 ;
; 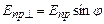 .
.
Перше коливання з амплітудою 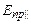 пройде через поляризатор, а друге з амплітудою
пройде через поляризатор, а друге з амплітудою 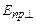 буде затримане поляризатором. Отже, при цьому
буде затримане поляризатором. Отже, при цьому 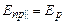 . Оскільки інтенсивність світла
. Оскільки інтенсивність світла 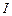 пропорційна квадратові амплітуди світлового вектора
пропорційна квадратові амплітуди світлового вектора 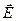 (
(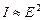 ), то співвідношення
), то співвідношення 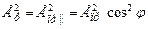 можна записати таким чином:
можна записати таким чином:
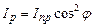 , (2.38)
, (2.38)
де 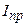 – інтенсивність коливань з амплітудою
– інтенсивність коливань з амплітудою 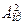 .
.
В природному світлі всі значення j рівноймовірні. Тому частка світла, що пройшло через поляризатор, буде дорівнювати середньому значенню 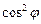 , тобто
, тобто 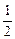 і
і
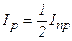 .
.
Якщо на аналізатор падає лінійно поляризоване світло, отримане за допомогою поляризатора, головна площина якого p–p утворює кут 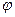 з головною площиною аналізатора a–a, то значення інтенсивності світла на виході з аналізатора буде виражатися формулою
з головною площиною аналізатора a–a, то значення інтенсивності світла на виході з аналізатора буде виражатися формулою
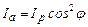 . (2.39)
. (2.39)
Якщо аналізатор і поляризатор не є абсолютно прозорими, то
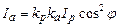 , (2.40)
, (2.40)
де 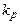 – кофіцієнт прозорості поляризатора,
– кофіцієнт прозорості поляризатора, 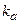 - коефіцієнт прозорості аналізатора.
- коефіцієнт прозорості аналізатора.
Отримані співвідношення (2.39) і (2.40) виражають закон Малюса.
З співвідношень (2.39) та (2.340) випливає, що зі зміною кута 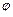 між головними площинами поляризатора і аналізатора змінюється інтенсивність світла
між головними площинами поляризатора і аналізатора змінюється інтенсивність світла 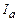 : якщо
: якщо 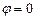 , то після аналізатора буде спостерігатися максимальна інтенсивність світла (світло повністю проходить через аналізатор), якщо
, то після аналізатора буде спостерігатися максимальна інтенсивність світла (світло повністю проходить через аналізатор), якщо 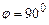 , то
, то 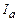 =0 − мінімальна інтенсивність світла (світло повністю гаситься).
=0 − мінімальна інтенсивність світла (світло повністю гаситься).
§2.3.2. Поляризація світла при відбиванні. Закон Брюстера
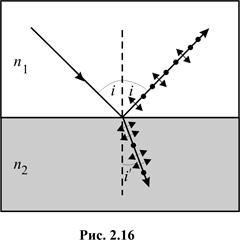 Якщо природне світло падає на межу поділу двох діелектриків, наприклад, повітря і скла, то частина його відбивається, а частина заломлюється і поширюється у другому середовищі. При цьому відбитий і заломлений промені частково поляризовані: при повертанні аналізатора навколо променів інтенсивність світла періодично посилюється і ослаблюється, але повного гасіння не спостерігається.
Якщо природне світло падає на межу поділу двох діелектриків, наприклад, повітря і скла, то частина його відбивається, а частина заломлюється і поширюється у другому середовищі. При цьому відбитий і заломлений промені частково поляризовані: при повертанні аналізатора навколо променів інтенсивність світла періодично посилюється і ослаблюється, але повного гасіння не спостерігається.
Дослідження показали, що у відбитому промені переважають коливання, перпендикулярні до площини падіння (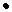 ), а в заломленому – коливання, паралельні площині падіння (
), а в заломленому – коливання, паралельні площині падіння ( ) (рис. 2.16).
) (рис. 2.16).
Ступінь виділення світлових хвиль з певною орієнтацією електричного вектора залежить від кута падіння променів і показника заломлення 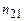 .
.
Відбитий промінь є повністю лінійно поляризованим в площині, яка перпендикулярна площині падіння променя, якщо кут падіння 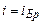 задовольняє умову
задовольняє умову
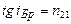 , (2.41)
, (2.41)
де 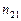 - показник заломлення другого середовища відносно першого.
- показник заломлення другого середовища відносно першого.
Цей закон називається законом Брюстера, а кут 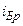 - кутом Брюстера. Ступінь поляризації заломленого променя при куті падіння
- кутом Брюстера. Ступінь поляризації заломленого променя при куті падіння 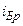 досягає найбільшого значення, проте цей промінь залишається поляризованим лише частково.
досягає найбільшого значення, проте цей промінь залишається поляризованим лише частково.
Відбивання природного світла під кутом Брюстера дає змогу отримати лінійно поляризоване світло, однак його інтенсивність невелика і для скла (n= 1,5) дорівнює близько 15%, тобто основна його частина поширюється у напрямку заломленої хвилі, яка поляризована не повністю. Для збільшення ступеня поляризації заломлених хвиль їх треба пропустити крізь набір скляних пластинок.
Так, для  набір з десяти скляних пластинок дає змогу отримати майже стопроцентну поляризацію заломлених хвиль.
набір з десяти скляних пластинок дає змогу отримати майже стопроцентну поляризацію заломлених хвиль.
§2.3.3. Обертання площини поляризації світла
Явище обертання площини поляризації світлової хвилі на деякий кут при проходженні світла крізь кристалічні тіла і деякі ізотропні рідини, називається обертанням площини поляризації або оптичною активністю.
Якщо речовина не знаходиться у зовнішньому магнітному полі, то оптична активність буде природною.
Нехай погляд спостерігача спрямований назустріч падаючому променю. Обертання називають правим (додатним), якщо площина поляризації повертається вправо (за годинниковою стрілкою) для спостерігача, і лівим (від’ємним), якщо вона повертається вліво. Кут обертання площини поляризації пропорційний до товщини шару оптично активної речовини:
 , (2.42)
, (2.42)
де 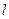 – довжина шляху променя в оптично активному середовищі;
– довжина шляху променя в оптично активному середовищі; 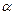 – коефіцієнт пропорційності, який називають обертальною здатністю, або питомим обертанням, залежить від природи речовини, від температури та довжини хвилі світла.
– коефіцієнт пропорційності, який називають обертальною здатністю, або питомим обертанням, залежить від природи речовини, від температури та довжини хвилі світла.
Питоме обертання 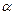 дорівнює величині кута, на який повертається площина поляризації монохроматичного світла при проходженні шару завтовшки 1 м.
дорівнює величині кута, на який повертається площина поляризації монохроматичного світла при проходженні шару завтовшки 1 м.
Для оптично активних рідин та розчинів Ж.Біо встановив, що кут повороту площини поляризації прямо пропорційний товщині шару l і концентрації C оптично активної речовини, тобто
 , (2.43)
, (2.43)
Коефіцієнт пропорційності 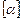 називається питомим обертанням розчину залежить від природи оптично активної речовини, розчинника, їх температури та довжини світлової хвилі.
називається питомим обертанням розчину залежить від природи оптично активної речовини, розчинника, їх температури та довжини світлової хвилі.
Властивості оптичної активності розчинів дають змогу визначити їх концентрації. Прилади, за допомогою яких проводять такі вимірювання, називаються поляриметрами. Оскільки для розчину цукру питоме обертання 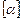 значне, то поляриметри набули широкого застосування в цукрометрії.
значне, то поляриметри набули широкого застосування в цукрометрії.
Теорію обертання площини поляризації оптично активними речовинами розробив О. Френель. Він вважав, що це явище зумовлене особливим видом подвійного заломлення променів, при якому швидкість поширення світла в активному середовищі різна для променів, що мають праву і ліву колові поляризації.
У 1845 р. М. Фарадей встановив, що при поширенні лінійно поляризованого світла в оптично неактивних речовинах в напрямку магнітного поля відбувається поворот площини поляризації на деякий кут. Досліди М. Фарадея та М. Верде показали, що кут повертання площини поляризації пропорційний довжині шляху l променя у речовині і напруженості 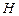 магнітного поля, тобто
магнітного поля, тобто
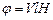 , (2.44)
, (2.44)
де V – стала Верде, яка залежить від природи речовини і довжини хвилі світла.
Сталу Верде для оптично неактивних рідин можна визначити, якщо розмістити трубку з рідиною в соленоїді і пропустити через його обмотку струм. Тоді напруженість магнітного поля всередині соленоїда (рідині) визначається з формули
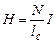 , (2.45)
, (2.45)
де 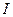 – сила струму, що протікає через соленоїд,
– сила струму, що протікає через соленоїд, 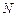 – кількість витків соленоїда,
– кількість витків соленоїда, 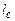 – довжина соленоїда.
– довжина соленоїда.
З врахуванням останньої формули отримаємо, що при умові 
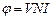 . (2.46)
. (2.46)
Згідно (2.46) графік залежності 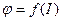 має вигляд прямої лінії, з нахилу якої
має вигляд прямої лінії, з нахилу якої 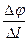 можна вирахувати сталу Верде
можна вирахувати сталу Верде
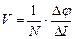 . (2.47)
. (2.47)
§2.4. Дисперсія світла
Дисперсією світла називається залежність показника заломлення n середовища від частоти 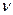 (довжини хвилі
(довжини хвилі 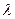 ) світла або залежність фазової швидкості
) світла або залежність фазової швидкості 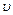 світла в середовищі від його частоти
світла в середовищі від його частоти 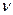 .
.
Дисперсію світла представляють у вигляді залежності 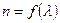 . Наслідком дисперсії є розклад у спектр пучка білого світла.
. Наслідком дисперсії є розклад у спектр пучка білого світла.
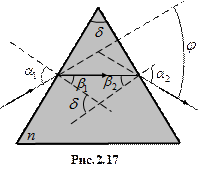
Розглянемо дисперсію світла у призмі. Нехай монохроматичний пучок світла падає на призму з показником заломлення n під кутом  (рис. 2.17). Кут
(рис. 2.17). Кут 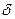 – заломлюючий кут призми. Із рис. 2.17 видно, що кут відхилення
– заломлюючий кут призми. Із рис. 2.17 видно, що кут відхилення 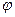 дорівнює:
дорівнює:
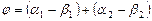
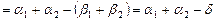 .
.
Нехай кути 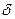 і
і 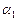 малі, тоді кути
малі, тоді кути 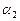 ,
, 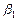 і
і 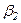 також будуть малі і синуси цих кутів дорівнюватимуть кутам. Тому
також будуть малі і синуси цих кутів дорівнюватимуть кутам. Тому
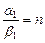 ,
, 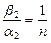 .
.
Оскільки 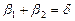 , то
, то
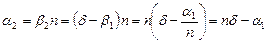 ,
,
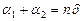 і
і 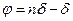 .
.
В результаті
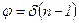 , (2.48)
, (2.48)
тобто кут відхилення променів призмою тим більший, чим більший заломлюючий кут призми. Оскільки кут відхилення 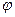 залежить від величини
залежить від величини 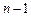 , а n є функцією довжини хвилі, то промені різних довжин хвиль після проходження призми виявляються відхиленими на різні кути.
, а n є функцією довжини хвилі, то промені різних довжин хвиль після проходження призми виявляються відхиленими на різні кути.
Кутовою дисперсією призми, що відповідає сталому значенню кута падіння  , називається величина
, називається величина
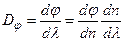 . (2.49)
. (2.49)
Кут відхилення 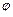 буде мінімальним, коли промінь проходить через призму паралельно до її основи. За такої умови
буде мінімальним, коли промінь проходить через призму паралельно до її основи. За такої умови 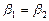 і
і 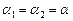 , тоді
, тоді
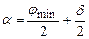 , а
, а 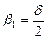 .
.
Згідно із законом заломлення
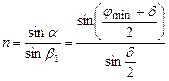 . (2.50)
. (2.50)
Звідси
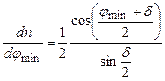 .
.
Тоді
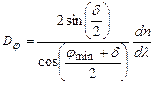
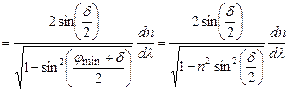 . (2.51)
. (2.51)
Для спектральних приладів призми виготовляють здебільшого із заломлюючими кутами 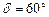 . Тоді
. Тоді
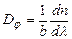 , де
, де 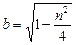 . (2.52)
. (2.52)
За допомогою призми, як і за допомогою дифракційної гратки можна визначити спектральний склад світла.
Величина, яка показує, як швидко змінюється показник заломлення п речовини з довжиною хвилі 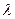 називається дисперсією речовини D:
називається дисперсією речовини D:
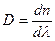 . (2.53)
. (2.53)
Дисперсію світла в середовищі називають нормальною, якщо із зростанням частоти 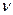 світла абсолютний показник заломлення n середовища також зростає:
світла абсолютний показник заломлення n середовища також зростає:
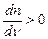 ,
, 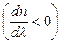 .
.
Така залежність показника заломлення n від 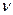 буде в тих областях частот, для яких середовище прозоре. Наприклад, звичайне скло прозоре для видимого світла і в цьому інтервалі частот має нормальну дисперсію.
буде в тих областях частот, для яких середовище прозоре. Наприклад, звичайне скло прозоре для видимого світла і в цьому інтервалі частот має нормальну дисперсію.
Дисперсію світла в середовищі називають аномальною, якщо із зростанням частоти 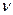 світла абсолютний показник заломлення середовища n зменшується:
світла абсолютний показник заломлення середовища n зменшується:
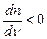 ,
, 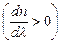 .
.
Аномальна дисперсія буде в області частот, які відповідають смугам інтенсивного поглинання світла речовиною
В різних ділянках спектра дисперсія характеризується тією зміною показника заломлення, яка припадає на одиничний інтервал довжин хвиль. Ця величина 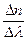 називається середньою дисперсією для ділянки спектра
називається середньою дисперсією для ділянки спектра 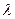 ,
, 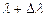 .
.
У довідникових таблицях показники заломлення 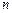 різних речовин даються для жовтої лінії натрію
різних речовин даються для жовтої лінії натрію 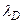 = 0,5893 мкм і позначаються
= 0,5893 мкм і позначаються 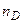 . Середня дисперсія визначається за синьою
. Середня дисперсія визначається за синьою 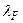 =0,4861 мкм і червоною
=0,4861 мкм і червоною 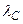 =0,6563 мкм лініях водню і позначається
=0,6563 мкм лініях водню і позначається 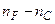 . Величина
. Величина 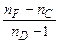 називається відносною дисперсією, обернена її величина – коефіцієнтом дисперсії.
називається відносною дисперсією, обернена її величина – коефіцієнтом дисперсії.
§2.5. Поглинання світла
Поглинанням світла називається явище втрати енергії світловою хвилею, яка проходить через речовину, внаслідок перетворення енергії хвилі у інші форми енергії.
При проходженні паралельного пучка світла крізь шар прозорого середовища його інтенсивність зменшується. Поглинання світла може приводити до нагрівання, іонізації або збудження атомів і молекул речовини, до деформації. Поглинання може супроводжуватись розсіянням світла та індуктивним випромінюванням.
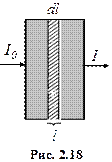 Щоб одержати співвідношення, яке виражає закон поглинання світла, розглянемо шар прозорого середовища завтовшки l, на який падає паралельний пучок променів інтенсивністю
Щоб одержати співвідношення, яке виражає закон поглинання світла, розглянемо шар прозорого середовища завтовшки l, на який падає паралельний пучок променів інтенсивністю 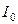 (рис. 2.18). Виділимо в середовищі нескінченно тонкий шар dl, який обмежений паралельними поверхнями, що перпендикулярні до напрямку поширення світла. Дослід показує, що зменшення інтенсивності світла шаром середовища dl пропорційне до величини інтенсивності, що входить у цей шар, і товщини шару, тобто
(рис. 2.18). Виділимо в середовищі нескінченно тонкий шар dl, який обмежений паралельними поверхнями, що перпендикулярні до напрямку поширення світла. Дослід показує, що зменшення інтенсивності світла шаром середовища dl пропорційне до величини інтенсивності, що входить у цей шар, і товщини шару, тобто
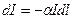 ,
,
де 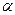 – коефіцієнт пропорційності, який не залежить від інтенсивності світла і називається коефіцієнтом поглинання.
– коефіцієнт пропорційності, який не залежить від інтенсивності світла і називається коефіцієнтом поглинання.
Знак мінус вказує на те, що із збільшенням товщини шару поглинаючого середовища інтенсивність світла, що проходить крізь нього, зменшується.
Після розділення змінних у рівнянні дістаємо
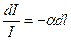 .
.
Проінтегруємо це рівняння:
 ;
; 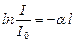 .
.
В результаті маємо, що
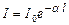 , (2.54)
, (2.54)
де І – інтенсивність світла, що виходить із шару поглинаючого середовища завтовшки l.
При 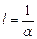 інтенсивність
інтенсивність 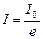 . Отже, шар, товщина якого дорівнює
. Отже, шар, товщина якого дорівнює 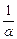 , зменшує інтенсивність світла в е разів. Співвідношення (2.54) було встановлене у 1729 р. П. Бугером і називається законом Бугера, або законом Бугера-Ламберта.
, зменшує інтенсивність світла в е разів. Співвідношення (2.54) було встановлене у 1729 р. П. Бугером і називається законом Бугера, або законом Бугера-Ламберта.
А. Бер встановив, що поглинання світла розчинами пропорційне молекулярній концентрації 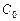 розчиненої речовини, тобто
розчиненої речовини, тобто
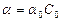 ,
,
де 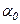 – коефіцієнт пропорційності. який залежить від природи розчиненої речовини і не залежить від її концентрації.
– коефіцієнт пропорційності. який залежить від природи розчиненої речовини і не залежить від її концентрації.
Тоді закону Бугера-Ламберта-Бера, який справедливий для газів і розчинів малих концентрацій, можна надати вигляду
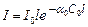 . (2.55)
. (2.55)
Рекомендована література до Розділу ІІ
1. І.Р. Зачек, І.М. Кравчук, Б.М. Романишин, В.М. Габа, Ф.М. Гончар. Курс фізики: Навчальний підручник/ За ред. І.Е. Лопатинського. – Львів: Бескид-Біт, 2002. 376 с.
2. Б.М. Яворський, А.А. Детлаф. Курс фізики ІІІ, - К.: Вища школа, 1973. 499 с.
3. Т.И. Трофимова. Курс физики. – М.: Высш шк., 1990. 478 с.
4. И.В. Савельев. Курс общей физики, т. ІІІ - М.: Наука, 1986. 318 с.
5. С.Э. Фриш, А.В. Тиморева. Курс общей физики, т. ІІІ. – М.: Физматгиз, 1962. 644 с.
Date: 2015-05-04; view: 1041; Нарушение авторских прав