
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Смуги однакового нахилу
|
|
Явище інтерференції світла можна спостерігати при падінні світлового променя на плоско–паралельну пластинку. В цьому випадку інтерференція світла визначається товщиною 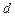 , показником заломлення n пластинки, довжиною
, показником заломлення n пластинки, довжиною 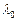 падаючої світлової хвилі та кутом падіння і. Для даних
падаючої світлової хвилі та кутом падіння і. Для даних 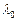 , d i n кожному куту i падіння променів відповідає своя інтерференційна смуга.
, d i n кожному куту i падіння променів відповідає своя інтерференційна смуга.
 Інтерференційні смуги, які виникають внаслідок накладання хвиль, що падають на плоскопаралельну пластинку під однаковими кутами, називаються смугами однакового нахилу.
Інтерференційні смуги, які виникають внаслідок накладання хвиль, що падають на плоскопаралельну пластинку під однаковими кутами, називаються смугами однакового нахилу.
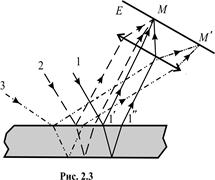
Інтерференційні смуги однакового нахилу, наприклад, можна одержати освітлюючи плоскопаралельну пластинку розбіжним пучком світла (рис. 2.3). Промені 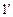 і
і 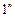 , відбившись від верхньої та нижньої граней пластинки, паралельні один до одного та інтерферують. Вони перетинаються в нескінченності, тому кажуть, що смуги однакового нахилу локалізовані в нескінченності.
, відбившись від верхньої та нижньої граней пластинки, паралельні один до одного та інтерферують. Вони перетинаються в нескінченності, тому кажуть, що смуги однакового нахилу локалізовані в нескінченності.
Для їх спостереження використовують збиральну лінзу та екран, який розміщений у фокальній площині лінзи. Паралельні промені 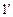 і
і 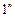 зберуться у фокусі лінзи (точці М). В ту саму точку прийдуть також інші промені, паралельні до променя 1, (на рис. 2.3. – промінь 2) внаслідок чого збільшиться загальна інтенсивність світла в точці
зберуться у фокусі лінзи (точці М). В ту саму точку прийдуть також інші промені, паралельні до променя 1, (на рис. 2.3. – промінь 2) внаслідок чого збільшиться загальна інтенсивність світла в точці 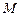 .
.
Промені, наприклад 3, які падають на пластину під іншим кутом, зберуться в іншій точці 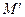 фокальної площини лінзи.
фокальної площини лінзи.
В точці M або 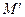 буде інтерференційний максимум, якщо виконується умова:
буде інтерференційний максимум, якщо виконується умова:
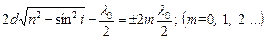 (2.7)
(2.7)
і мінімум, якщо:
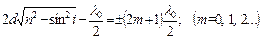 . (2.8)
. (2.8)
Інтерференційні смуги рівного нахилу при великій оптичній різниці ходу променів можна спостерігати для монохроматичного лазерного випромінювання. Для цього використовують світловий потік з великою розбіжністю, який одержують наприклад за допомогою мікрооб’єктива О, і направляють на скляну плоскопаралельну пластину П (рис. 2.4). Промені, відбиті від передньої і задньої граней плоскопаралельної пластини, дають інтерференційні смуги рівного нахилу на екрані Е у вигляді концентричних кілець
Нехай кути 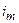 , при яких спостерігаються мінімуми інтенсивності
, при яких спостерігаються мінімуми інтенсивності 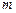 –го порядку у відбитому світла, визначаються з умов (2.8), або
–го порядку у відбитому світла, визначаються з умов (2.8), або
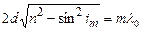 ,
, 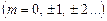 . (2.9)
. (2.9)
Якщо кути 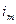 малі, то
малі, то 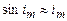 і рівняння (2.9) можна записати таким чином:
і рівняння (2.9) можна записати таким чином:
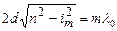 ,
,
або
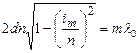 . (2.10)
. (2.10)
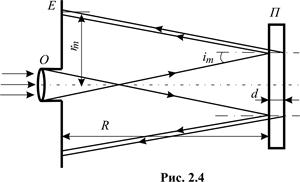
З рис. 2.4 випливає, що 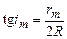 , де R – відстань від екрана до поверхні плоскопаралельної пластини,
, де R – відстань від екрана до поверхні плоскопаралельної пластини, 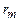 – радіус темного кільця. Так як кут
– радіус темного кільця. Так як кут 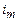 є малим, то
є малим, то  . Отже
. Отже
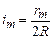 . (2.11)
. (2.11)
Підставивши значення 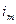 у формулу (2.10) отримаємо:
у формулу (2.10) отримаємо:
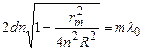 . (2.12)
. (2.12)
Рівняння (2.12) можна замінити виразом
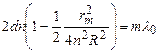 .
.
Звідки
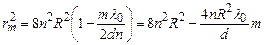 . (2.13)
. (2.13)
Як видно з (2.13), 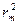 лінійно залежить від порядку
лінійно залежить від порядку 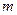 темного інтерференційного кільця. Для довільно вибраних кілець, згідно із співвідношення (2.13), випливає, що
темного інтерференційного кільця. Для довільно вибраних кілець, згідно із співвідношення (2.13), випливає, що
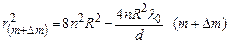
і
 ,
,
де 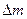 – різниця між номерами інтерференційних кілець.
– різниця між номерами інтерференційних кілець.
Нехай 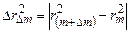 . Тоді
. Тоді
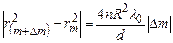 .
.
Звідки отримуємо, що
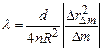 , (2.14)
, (2.14)
або
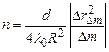 . (2.15)
. (2.15)
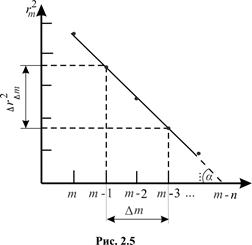
Якщо побудувати графік залежності 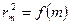 за рівнянням (2.13) (див. рис. 2.5), то тангенс кута нахилу цієї прямої дорівнює коефіцієнту при
за рівнянням (2.13) (див. рис. 2.5), то тангенс кута нахилу цієї прямої дорівнює коефіцієнту при 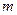 у цьому рівнянні:
у цьому рівнянні:
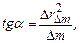
де 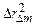 – різниця квадратів радіусів відповідних кілець;
– різниця квадратів радіусів відповідних кілець; 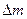 - різниця номерів кілець.
- різниця номерів кілець.
Підставивши значення 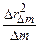 , R, n, d у формулу (2.14) можна розрахувати довжину хвилі
, R, n, d у формулу (2.14) можна розрахувати довжину хвилі 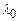 випромінювання лазера. Якщо в (2.15) підставити відомі значення
випромінювання лазера. Якщо в (2.15) підставити відомі значення 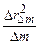 , R,
, R, 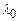 ,
, 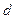 , то можна отримати значення показника заломлення
, то можна отримати значення показника заломлення 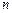 плоскопаралельної пластини.
плоскопаралельної пластини.
На цьому базується графічний метод визначення довжини хвилі, або показника заломлення скляної пластинки.
§2.1.4. Смуги однакової товщини
Нехай на клин, кут 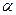 між боковими гранями якого малий, падає плоска хвиля, напрямок поширення якої збігається з променями 1 і 2 (рис. 2.6).
між боковими гранями якого малий, падає плоска хвиля, напрямок поширення якої збігається з променями 1 і 2 (рис. 2.6).
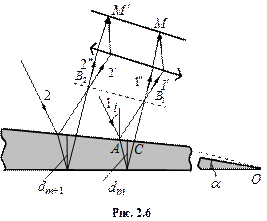
Напрямок поширення інтерферуючих хвиль, які виникають внаслідок відбивання світла від верхньої і нижньої поверхонь клина зображено відповідно променями 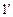 і
і 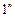 та
та 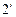 і
і 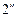 .
.
Якщо джерело хвиль розміщене далеко від поверхні, а кут 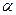 досить малий, то оптична різниця ходу променів
досить малий, то оптична різниця ходу променів 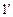 і
і 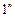 визначається за формулою
визначається за формулою
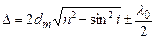 , (2.16)
, (2.16)
де 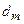 – середня товщина клина на ділянці АС;
– середня товщина клина на ділянці АС; 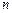 – показник заломлення клина;
– показник заломлення клина; 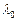 – довжина падаючої світлової хвилі;
– довжина падаючої світлової хвилі; 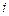 – кут падіння світлової хвилі.
– кут падіння світлової хвилі.
Оскільки значення i, n та 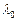 сталі, то однаковим значенням dm відповідають однакові оптичні різниці ходу. В (2.16) беруть знак “+”, якщо показник заломлення
сталі, то однаковим значенням dm відповідають однакові оптичні різниці ходу. В (2.16) беруть знак “+”, якщо показник заломлення 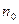 середовища є більшим ніж показник заломлення
середовища є більшим ніж показник заломлення 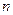 матеріалу клина і “–“, якщо показник заломлення
матеріалу клина і “–“, якщо показник заломлення 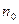 середовища є меншим ніж показник заломлення
середовища є меншим ніж показник заломлення 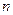 матеріалу клина.
матеріалу клина.
При певному положенні лінзи і клина промені 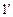 та
та 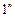 збігаються в деякій точці M на екрані та інтерферують. А всі промені, які падають на поверхню клина товщиною
збігаються в деякій точці M на екрані та інтерферують. А всі промені, які падають на поверхню клина товщиною 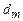 , будуть в результаті інтерференції утворювати інтерференційну смугу.
, будуть в результаті інтерференції утворювати інтерференційну смугу.
Інтерференційні смуги, що виникають внаслідок відбивання від ділянок клина з однаковою товщиною, називаються смугами однакової товщини.
Оскільки верхня та нижня грані клина не паралельні між собою, то промені 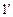 і
і 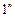 та
та 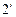 і
і 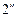 перетинаються поблизу поверхні клина. Лінія перетину
перетинаються поблизу поверхні клина. Лінія перетину 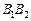 всіх променів проходить через вершину O клина. Отже, смуги однакової товщини локалізовані поблизу поверхні клина.
всіх променів проходить через вершину O клина. Отже, смуги однакової товщини локалізовані поблизу поверхні клина.
§2.1.5. Кільця Ньютона
Для утворення кілець Ньютона паралельний пучок світла направляють нормально на плоску поверхню BC з великим радіусом R кривизни плоскоопуклої лінзи, яка дотикається в точці M до плоскої скляної пластинки (рис. 2.7). Після відбивання від опуклої поверхні лінзи і дотичної до неї поверхні пластини світло поширюється у зворотному напрямку паралельним пучком. При накладанні відбитих хвиль виникають інтерференційні смуги однакової товщини. Оскільки результат накладання двох відбитих хвиль залежить від товщини прошарку між лінзою і скляною пластиною, то для всіх точок, що знаходяться на однаковій відстані r від точки M, тобто тих, що утворюють коло, буде однакова умова для інтерференційного максимуму, або мінімуму.
Нехай d – товщина повітряного прошарку на відстані r від точки M (рис. 2.7). Оптична різниця ходу Δ між променем, який відбився від межі поділу повітряний шар – скляна пластина, і променем, який зазнав часткового відбивання на межі поділу опукла поверхня лінзи – повітряний шар, дорівнює
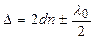 , (2.17)
, (2.17)
де доданок 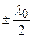 враховує втрату півхвилі при відбиванні світла.
враховує втрату півхвилі при відбиванні світла.
Так як лінза і пластина виготовлені зі скла, показник заломлення якого 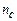 більший від показника заломлення
більший від показника заломлення 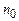 повітря, то
повітря, то 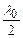 буде зі знаком “+”.
буде зі знаком “+”.
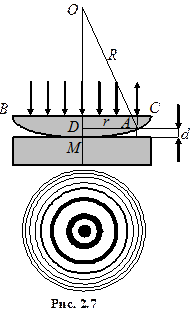 Якщо прийняти
Якщо прийняти 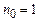 , то можна показати [1], що радіус m –го світлого кільця Ньютона, виходячи з умови інтерференційних максимумів для відбитого світла, становить
, то можна показати [1], що радіус m –го світлого кільця Ньютона, виходячи з умови інтерференційних максимумів для відбитого світла, становить
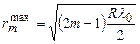 ; (m= 1, 2, 3, …) (2.18)
; (m= 1, 2, 3, …) (2.18)
а радіус m -го темного кільця для відбитого світла визначається з умови:
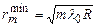 ;
;  . (2.19)
. (2.19)
В прохідному світлі
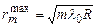 ; (m= 0, 1, 2, 3 …), (
; (m= 0, 1, 2, 3 …), (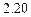 )
)
а
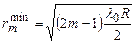 ; (m= 1, 2, 3 …). (
; (m= 1, 2, 3 …). (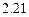 )
)
В співвідношеннях (2.18), (2.19), (2.20) і (2.21) 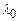 –довжина монохроматичної хвилі у вакуумі;
–довжина монохроматичної хвилі у вакуумі; 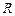 – радіус кривизни опуклої поверхні лінзи.
– радіус кривизни опуклої поверхні лінзи.
§2.2. Дифракція світла
Date: 2015-05-04; view: 1324; Нарушение авторских прав