Определение индикаторов подобия методом анализа уравнений

Сущность метода рассмотрим на примере балки, нагруженной произвольной нагрузкой и испытывающей поперечный изгиб.

Воспользуемся уравнением изогнутой оси балки в общем виде:

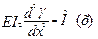. (4.9)

Очевидно, что это уравнение в равной мере описывает закон деформирования, как прототипа, так и его модели. При этом подобие деформации и усилий будет обеспечено, если в обоих уравнениях будет соблюдено соотношение сходственных величин, т. е. их масштабов. Опустив дифференциальные операторы и заменив параметры всех величин их масштабами, получим уравнение:

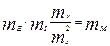. (4.10)

Изгибающие моменты в правой части уравнения (4.9) могут быть заменены сводными функциями от конкретной нагрузки на балку. Так, например, при любой погонной нагрузке q(x) можно представить уравнение изгибающих моментов в виде:

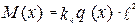. (4.11)

Заменив конкретные параметры масштабами преобразований, получим уравнение:

. (4.12)

В этом уравнении опущен масштаб т_k, который равен единице, поскольку является отношением равных чисел.

Масштабы линейных преобразований принимаем одинаковыми по всем направлениям, а именно m_х = m_v = m_z =m_l, тогда m₁ = т_l⁴ (так как размерность момента инерции см⁴). Подставив в (4.10), с учетом (4.12), получим:

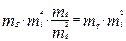(4.13)

или окончательно:

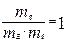. (4.14)

Полученный индикатор подобия при распределенной нагрузке q(x) в точности совпадает с аналогичным в формуле (4.8), полученным методом анализа размерностей.

Если балка нагружена сосредоточенными силами Р_i, то функцию изгибающих моментов можно представить в виде уравнения:

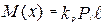. (4.15)

Заменив конкретные параметры их масштабам, учитывая, что т_k= 1, сделав преобразования уравнения (4.10) аналогичнопредыдущему, получим критерий подобия:

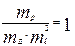, (4.16)

который в точности совпадает с аналогичным в формуле (4.8). К такому же выводу мы придем, рассматривая конструкции, нагруженные поверхностной нагрузкой, если будем оставаться в пределах гипотез простого подобия.

В заключение еще раз сформулируем необходимые и достаточные условия простого подобия при моделировании задач теории упругости:

1) модель и прототип должны быть геометрически подобными;

2) коэффициенты Пуассона для материала модели и материала прототипа должны быть равны;

3) материал модели должен быть упругим, его выбор обусловливает значение масштаба модулей;

4) все нагрузки на модель должны находиться в таком же соотношении между собой, как и соответствующие нагрузки, действующие на прототип;

5) поскольку масштаб т_Е определен выбором материала для модели, то для произвольного выбора остаются только масштабы т_l либо масштаб одной из нагрузок, например т_p, остальные вычисляют, используя индикаторы подобия.

Date: 2015-06-06; view: 1021; Нарушение авторских прав