Сущность механического моделирования. Понятие о теории подобия

Подобными в механическом смысле называют такие деформируемые системы, которые являются подобными геометрически и у которых напряжения, деформации, перемещения и другие исследуемые величины в сходственных точках в сходные моменты времени могут быть выражены через определенные соотношения, называемые масштабами перехода.

Теория подобия, лежащая в основе механического моделирования, изучает закономерности соотношений между геометрическими размерами прототипа исследуемой конструкции, так называемой натуры, и её модели, механическими константами материалов, величинами нагрузок, напряжениями и деформациями прототипа и модели.

Условия подобия, согласно этой теории, устанавливают двояким образом. Первый заключается в анализе размерностей величин, относящихся к исследуемому процессу. Если прототип или исследуемый процесс мало изучены, то можно составить для них только перечень описывающих параметров, характеризующих этот процесс и имеющих одинаковые размерности, как у прототипа, так и у его модели. Второй способ исходит из анализа уравнений, описывающих данный процесс, рассматривает поведение объекта при различных воздействиях с учётом реальных граничных условий. Этот способ считается более корректным. В последующем мы познакомимся с каждым из названных способов и убедимся, что результаты, определяющие условия подобия, в конечном счёте получаются одинаковыми.

Вспомним основные параметры, которые в общем случае могут входить в уравнение равновесия и влияют на напряжённо-деформированное состояние конструкций в стадии упругой работы. В квадратных скобках покажем символически их размерность, например, для всех линейных величин l_i [L], для сосредоточенных и любых продольных сил P_j[P], модулей упругости E _i [ PL ^-2] - размерность напряжения и т. д.

Геометрию конструкции, ее элементов характеризуют линейные размеры l_i [L] и соотношения между ними. Основными видами нагрузок могут быть - P_j [ P ] сосредоточенные силы; M_i [ PL ] - сосредоточенные моменты; q_i[PL^-1] - погонная (распределенная по длине); q_i [ PL^-1 ] - распределенная по поверхности конструкции.

Механические свойства упругих материалов характеризуются модулями упругости E_i [ PL^-2 ] и коэффициентами Пуассона µ_i, которые не имеют размерности. Относительные фибровые деформации ε_i, также величины безразмерные.

Общим недостатком представления моделируемых параметров в размерном виде является то, что численные величины и соотношения между ними изменяются в зависимости от принятой системы единиц - СИ, метрической или какой-нибудь иной. Поэтому в дальнейшем, ради удобства анализа, от размерных параметров перейдем к безразмерным.

В зависимости от сложности задач, решаемых методом моделирования, и принятых исходных предпосылок различают два вида подобия - простое, или строгое, и расширенное, или неполное. Различия между ними, достоинства и недостатки каждого отметим, ознакомившись с их особенностями.

Простое подобие упругих деформируемых систем. Метод анализа размерностей

Среди приведенных выше параметров, имеющих размерность, в качестве независимых общих удобно принять два, например l и Е, и через них путём анализа размерностей и простых преобразований перейти к безразмерным комплексам. Обязательным условием простого (строгого) подобия является равенство всех полученных таким образом безразмерных комплексов для прототипа и модели. Их одинаковость математически обозначают словом idem, что в переводе с латинского означает «одинаковый», «один и тот же». В такой форме совокупность критериев подобия модели и прототипа приобретает вид:

в отношении геометрии l = idem;

в отношении материалов Е = idem; µ = idem;

в отношении деформации ε = idem;

в отношении нагрузок получим безразмерные комплексы:

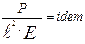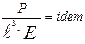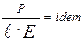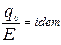; ; ; (4.2)

Критерий подобия l= idem означает, что модель в отношении геометрии должна быть подобна прототипу, т. е. все размеры модели и прототипа должны быть связаны единым масштабным множителем

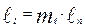. (4.3)

Критерии подобия безразмерных параметров µ = idem и ε = idem означают, что в сходственных точках модели и прототипа они должны быть одинаковыми, т. е.

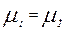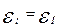; . (4.4)

Для линейного упругого материала это означает равенство отношений:

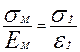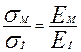или (4.5)

Эти и другие безразмерные отношения целесообразно заменить соответствующими масштабными множителями. Так, зависимости (4.4) и (4.5) можно записать в следующем виде:

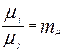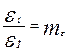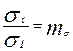; ; ; (4.6)

Из этих отношений, с учетом (4.4) и (4.5), получим:

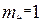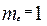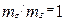; ; (4.7)

Соотношения вида (4.7) называются индикаторами подобия. При простом подобии все критерии подобия idem, выраженные через масштабные коэффициенты, также являются индикаторами подобия, равными единице, т. е.:

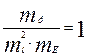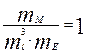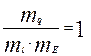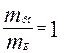; ; ; . (4.8)

Индикаторы (4.8) имеют важное значение, так как с их помощью находят соотношение между нагрузками, действующими на прототип и на модель в любых комбинациях. Рассмотрим некоторые частные случаи. Допустим, что масштабы т_l и т_E известны, т. е. размеры модели и материал, из которого она будет изготовлена, даны. Требуется рассчитать нагрузку на модель, а если нагрузки разные, то соотношение между ними.

Случай 1. К прототипу приложены только сосредоточенные силы Р_1П, Р_2П„ и т. д. Чему должны быть равны Р_1M; P_2M и т.д. в сходственных точках модели, чтобы выполнялись все критерии подобия?

Воспользуемся первым индикатором подобия (4.8), найдем т_р=т_Е·m²_l , а затем, зная т_р, определим P_iМ = P_iН ·т_р. Из последнего выражения следует также, что при нагружении модели на всех стадиях следует соблюдать закон пропорциональности и синхронности изменения нагрузок. Аналогично решается задача относительно любой схемы нагружения, предусмотренной индикаторами (4.8).

Случай 2. К прототипу приложены одновременно сосредоточенные силы P_1П, P_2П и погонные распределенные нагрузки q_1П, q_2П и т. д. Каково должно быть соотношение между интенсивностями нагрузок на модель, чтобы соблюдались все критерии подобия?

Из равенства левых частей первого и третьего критериев подобия (4.8) находим взаимосвязь m_p = m_q m_l.

Установив масштаб т_р без учета т_q, как в случае 1, находим m_q = т_р /т_l, а затем и сами нагрузки q_lM=q_iПm_q Аналогично решается задача при любом сочетании нагрузок.

Date: 2015-06-06; view: 1547; Нарушение авторских прав