
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методы решения нелинейных уравнений
|
|
Пусть задана непрерывная на интервале [ a,b ] функция f(x). Необходимо найти все или некоторые корни уравнения f(x)=0. Существует ряд методов решения этой задачи, которые сводятся к последовательному, пошаговому уточнению решения.
Дихотомия. Для применения этого метода задается интервал, на котором будет производится поиск корня. (см. рис. 3). Поиск начинается на интервале (x0,x1). Предполагается, что на этом интервале есть корень, т.е. f(x0)f(x1) <0. Интервал делится пополам точкой x2 = (x1-x0)/2. Затем производится поиск того из интервалов [ x1,x2 ], [ x2,x1 ], на котором находится корень. После этого анализа процедура повторяется до тех пор, пока не будет выполнено заранее заданное условие точности решения (либо (x1-x0<e, либо f((x1-x0)/2) <e).
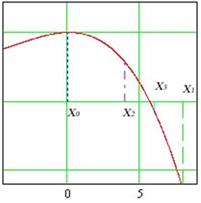
Рис. 3
Метод Ньютона. Этот метод применим, если известно выражение не только для самой функции, но и для ее первой производной. Выбирается начальное приближение x0, затем в точке f(x0) функция заменяется касательной к ней. После того, как найдена точка пересечения касательной с осью Х, эта точка принимается за новое приближение, после чего процесс повторяется.
Итерационный процесс можно описать следующим образом:
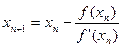
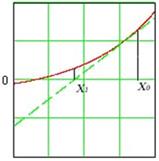
Рис.4
Метод секущих (метод хорд). Этот метод можно рассматривать как модификацию метода Ньютона для случая, когда производную от функции невозможно найти аналитически. Здесь точное значение производной заменяют ее приближенным значением, т.е. прямой, проведенной через точки xn-2 , xn-1 (для первого шага выбираются две точки). Итерационная формула выглядит следующим образом:

Date: 2015-06-06; view: 543; Нарушение авторских прав