Законы фильтрации (основы динамики подземных вод)

Законы движения подземных вод составляют предмет особой научной дисциплины - динамики подземных вод, которая в свою очередь является ча­стью подземной гидравлики, изучающей общие законы движения жидких и газообразных тел. Известно, что основная часть воды в земной коре переме­щается в связанном состоянии вместе с частицами горных пород внутри кри­сталлической решетки или на ее поверхности в виде целых молекул воды. Е.В.Пиннекер и С.Л. Шварцев движение воды вместе с горной породой называют геологическим движением воды, которое наряду с фильтрацией играет важную роль в геологической истории Земли. Таким образом, необходимо различать движение воды как самостоятельного физического тела, затем как тела физически или химически связанного с горными породами и в третьих как геологического тела [16].

Свободная вода, если она не связана силами с горными породами, ведет себя как самостоятельное физическое тело, подчиняясь законам гравитацион­ного, теплового и геофизического поля. Движение жидкой воды происходит в результате передачи гидростатического давления от участков более высокого напора к участкам его более низких значений. В этой связи свободная вода находится под влиянием только гидростатического давления, т.е. веса выше­лежащего столба воды:

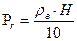(5.2)

где r_в - плотность воды; Н - глубина залегания измеряемой точки от уровня первого от поверхности земли водоносного горизонта.

Исследования, проведенные в нефтегазоносных районах, где были про­бурены глубокие скважины показали, что пластовые давления в водоносных горизонтах нередко выше расчетных гидростатических в 1,3-1,6 раза. Такое давление, обусловленное плотностью горных пород, назвали литостатиче-ским, что оказало влияние на разработку новых схем гидродинамической зо­нальности земных недр и типов гидродинамического режима: инфильтраци-онного типа, эллизионного типа (выжимающего воду из пород за счет их уп­лотнения) и глубинного типа (под действием геостатического и тектониче­ского давлений).

В настоящее время наиболее существенным является инфильтрацион-ный тип режима, в пределах которого движение подземных вод (безнапорных и напорных) происходит вследствие разности напоров в зоне современной инфильтрации и зоне разгрузки.

Движение жидкостей и газов (подземных флюидов) в породах и трещи­нах горных пород обусловленное наличием перепадов напоров называется фильтрацией. Основными гидродинамическими элементами фильтрационного потока являются: пьезометрический напор, напорный градиент, линии тока и линии равных напоров. Для простоты расчетов реальный поток жидкости, движущейся только через поровое пространство, заменяется фиктивным потоком занимающим весь водо­носный пласт, включая не только поровое пространство, но и скелет породы.

По определению русского ученого Д.Бернулли величина напора выра­жается уравнением:

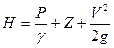(5.3)

где Р - гидростатическое давление в исследуемой точке потока; g - объемная масса воды; Z - высота исследуемой точки потока над выбранной плоскостью сравнения напоров; V²/2g - скоростной напор, который в потоке весьма мал и обычно приравнивается нулю. В этом случае

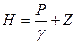(5.4)

Правая часть уравнения (5.3) известна под названием пьезометрическо­го напора, а отношение Р/g = h_p как пьезометрическая высота. В случае безна­порного потока пьезометрическая высота равна глубине погружения точки выбранной для замера от зеркала грунтовых вод, а в случае напорных вод -глубине погружения точки от пьезометрической поверхности этих вод (рис.). При горизонтальном залегании подошвы водоупора пьезометрический на­пор Н равняется мощности потока h.

При движении воды через поровое пространство часть напора теряется на трение, что создает уклон поверхности подземных вод в сторону их движения. У вод со свободной поверхностью в разрезе образуется кривая депрессий, а у напорных вод - пьезометрическая кривая. Средний уклон Iср кривой депрессии подземных вод равен

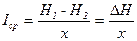(5.5)

где H₁ и Н₂ - напоры воды в любых двух сечениях; х - расстояние между этими сечениями.

Для потоков подземных вод характерно преобладание протяженности фильтрационного поля в плане над его мощностью при преимущественно го­ризонтальном направлении движения, что не исключает наличия, например, вертикального движения потоков. В зависимости от характера траектории движения воды различают одномерные (прямые линии), двухмерные (криволинейные) и трехмерные (пространственные кривые) потоки. Структу­ру потока представляет гидродинамическая сетка, которую образуют линии равных напоров и линии токов (рис).

В зависимости от поведения линий тока различают установившееся и неустановившееся движение. При установившемся движении параметры по­тока - мощность, напорный градиент и расход - не изменяются во времени, при неустановившемся эти параметры быстро изменяются и по величине и по направлению. Соответственно гидродинамическая сетка в условиях устано­вившегося движения будет постоянной во времени, в условиях неустановив­шегося - переменной.

В общем случае движение подземных вод - неустановившееся. Однако, при решении практических задач изменениями характеристик потока, если они незначительны, можно пренебречь. Считают, что на рассматриваемый расчетный момент времени в пределах определенной зоны устанавливается так называемый квазистационарный режим. Для этой зоны справедливы за­висимости, применяющиеся при стационарном (установившемся) режиме.

Потоки подземных вод имеют естественные границы. Нижней границей является водоупорное основание (горизонтальное или наклонное). Верхней границей потока является свободная поверхность воды (для безнапорных вод) или кровля водоупорного слоя (для напорных вод). Боковыми границами по­тока являются зоны его дренажа и питания. Ими могут быть реки, овраги, болота, озера. Если границы находятся на большом удалении от изучаемого участка, то поток рассматривается как неограниченный. Уравнения, описы­вающие фильтрационные процессы, их выбор для решения задач зависит от взаимного расположения и конфигурации границ водоносных пластов, а также условий на этих границах. Кроме того, должны быть известны т.н. на­чальные условия, т.е. распределение напоров (уровней) по области фильтра­ции. Простейшее условие на границе области фильтрации - постоянный на­пор, который характерен обеспеченным питанием водоносных горизонтов (граница первого рода). Чаще всего такие контуры представляют собой внешние границы дренируемых пластов. Горные и дренажные выработки могут обеспечивать постоянный напор и на внутренних границах дренажа. На непроницаемых контурах обычно задается нулевая скорость фильтрации, т.е. нулевой расход потока (граница второго рода). Такие границы могут быть при выклинивании водоносных горизонтов. На границах питания, дренажа или площади развития водоносных пластов может возникать перетекание через слабопроницаемые породы (граница третьего рода). В качестве примера можно привести условие, при котором в дренируемый пласт перетекает поток из водотока через слабопроницаемые породы или разгрузка водоносного горизонта при дренировании его горной выработкой отделенной слабопро­ницаемым экраном. Интенсивность такого перетока зависит от фильтраци-онных свойств экрана и перепада напоров на нем. Кроме приведенных трех разновидностей граничных условий выделяют условия четвертого рода, ко­торые фиксируются на разделе зон характеризующихся различными фильтра-ционными свойствами.

Отражение общих закономерностей фильтрации в совокупности с на­чальными и граничными условиями при решении уравнений движения пото­ков реализуется в определенной гидродинамической схеме.

В 1856 на основе опытов фильтрации воды через различные пористые среды, французский исследователь Анри Дарси установил закон движения подземных вод. Этот закон, получивший его имя, описывается уравнением

Q = К I F (5.6)

где К - коэффициент пропорциональности, зависящий от физических свойств породы и фильтрующейся жидкости; F - площадь поперечного сечения поро­ды.

Разделив обе части уравнения на F, получим

V = КI (5.7)

Уравнение выражает закон Дарси, отражающий линейную зависимость между скоростью фильтрации и напорным градиентом. Коэффициент К по­лучил название коэффициента фильтрации, который при гидравлическом градиенте равном единице, представляет собой скорость фильтрации. Раз­мерность коэффициента фильтрации та же, что и скорость фильтрации, т.е. см/с, м/ч или м/сут.

Для того, чтобы получить действительную скорость движения воды не­обходимо скорость фильтрации V разделить на эффективную пористость по­роды п:

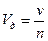(5.8)

Закон Дарси применим для движения воды в любом направлении и ха­рактеризует ламинарное движение воды в горных породах. В практике иссле­дований зафиксированы отклонения от закона Дарси, происходящие при больших скоростях движения подземных вод. При скоростях, характеризую­щихся критическими значениями числа Рейнольдса (2300), движение воды приобретает турбулентный (вихревой) характер. Однако, практически в во­доносных горизонтах отклонений от закона Дарси не наблюдается. Переход от ламинарного движения к турбулентному сопровождается отклонением от линейного закона фильтрации. Наряду с фильтрацией воды в горных породах имеет место ее конвекция - тепло- и массоперенос движущимися потоками вещества. Благодаря конвекции происходит перемещение тепла и растворен­ного вещества в горных породах. Кроме конвекции, перенос вещества проис­ходит вследствие т.н. молекулярной диффузии, ощутимое значение которой сказывается, если фильтрационный поток пренебрежимо мал по сравнению с диффузионным.

Для характеристики фильтрационных свойств горных пород наряду с коэффициентом фильтрации используется коэффициент водопроводимости Т, равный произведению коэффициента фильтрации на мощность водоносного горизонта.

К фильтрационным свойствам горных пород также относятся коэффи­циент уровнепроводности (для безнапорных вод) и коэффициент пьезопро-водности (для напорных вод), имеющие размерность м²/сут. Они характеризуют скорость перераспределения уровней воды или напоров в водоносном горизонте при возмущении в последнем.

К емкостным свойствам водоносного горизонта относят, помимо по­ристости, безразмерные коэффициенты гравитационной (безнапорные воды) и упругой (напорные воды) водоотдачи, а также коэффициент, учитывающий недостаток насыщения горных пород.

Коэффициент гравитационной водоотдачи (m) представляет собой от­ношение объема свободно вытекающей под действием гравитации воды к объему осушенной породы и численно равен коэффициенту недостатка на­сыщения. Обычно он равен 0,1-0,3 для песков и 0,01-0,1 для суглинков. Вели­чина упругой водоотдачи - количество воды, высвобождающейся с единицы площади при снижении напора на 1 м. Наличие упругих сил в водоносном пласте вызывает некоторое запаздывание реакции напора (неустановившийся режим).

Параметры водоносных горизонтов (коэффициентов фильтрации, во-допроводимости, уровнепроводности, пьезопроводности, гравитационной и упругой водоотдачи и др.) могут быть получены лабораторным методом, по данным режимных наблюдений и опытным путем. Опытные работы пред­ставляют собой различные виды откачек (пробные, опытные, опытно-эксплуаатционные и др.), наблюдения за режимом водоотлива и соответст­вующим положением уровней воды в горных выработках. Расчеты парамет­ров по данным опытных работ и режимных наблюдений выполняются, как правило, аналитическими, графоаналитическими и другими методами, а так­же с использованием ЭВМ.

Для оценки водопритоков к горным выработкам и дренажным соору­жениям используют следующие методы: гидрогеологических аналогий, вод­ного баланса и гидродинамический (аналитический, математического моде­лирования). Кроме того может быть использован гидравлический метод оценки.

Метод гидрогеологической аналогии основан на использовании пара­метров осушения уже разрабатываемого участка. Он, как правило, применя­ется для оценки водопритоков проектируемого горного предприятия. Оценка водопритоков методом водного баланса производится с помощью приходных и расходных элементов ресурсов подземных вод (осадки, инфильтрация, ис­парение, модуль стока, расход поверхностных водотоков и др.). Метод при­меняется, как правило, в сочетании с аналитическим и самостоятельно ис­пользуется редко. Наиболее распространенным является гидродинамический метод с использованием уравнений динамики подземных вод.

При постоянном дебите выработки (скважины) для расчетов понижений в любой точке напорного неограниченного пласта при неустановившемся ре­жиме фильтрации используют формулу:

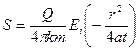(5.9)

где S - понижение уровня в выработке, м;

Q - водоприток, м³/сут;

k - коэффициент фильтрации, м/сут;

m - мощность напорного потока, м;

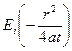- интегральная экспоненциальная функция, определяемая по

табличным данным;

г - радиус выработкам;

а - коэффициент пьезопроводности, м²/сут;

t - расчетный момент времени, сут.

При длительной эксплуатации выработок наблюдается т.н. квазиста­ционарный режим фильтрации и интегральная экспоненциальная функция в определенной зоне (при r²/4at £ 0,1) может быть заменена на логарифмиче­скую:

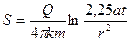(5.10)

Формула подобна известной для установившегося притока к скважине формуле Дюпюи,

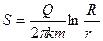(5.11)

а величину R = 1,5Öat нередко называют неустановившимся радиусом влияния выработки (скважины). При этом зона квазистационарного режима формируется в радиусе г < 0, 5 Öat.

Приведенные выше уравнения действительны для напорных вод. В слу­чае фильтрационных расчетов для безнапорных условий в формулах (3.10, 3.11) следует заменить величину m на (2H+h₀)/3 (где Н - мощность безнапор­ного водоносного горизонта, м; h0 - остаточная мощность водоносного гори­зонта, м).

Уравнение (5.9-5.11) позволяют решать фильтрационные задачи для одиночных выработок (скважин) в неограниченных условиях. Для расчета понижений при работе нескольких взаимодействующих скважин (или при ра­боте с переменным дебитом) и в ограниченных условиях используют принцип сложения течений (суперпозиции) и метод зеркальных отражений.

Принцип сложения течений заключается в том, что воздействие не­
скольких взаимодействующих скважин на фильтрационное поле может быть
оценено простым суммированием реакций от каждой скважины в отдельности. Так, суммарное понижение уровня в водоносном горизонте от нескольких взаимодействующих водопонижаюших скважин в какой-либо расчетной
точке (r) неограниченного пласта можно оценить по формуле:

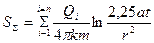(5.12)

где r_i - расстояние от скважины i до расчетной точки r;

Q – дебит скважины,

n - число скважин.

Принцип зеркальных отражений позволяет ограниченные и полуогра­ниченные фильтрационные поля привести к неограниченным условиям и ре­шить поставленную задачу, использовав принцип суперпозиции. Например, скважина расположена в пласте, ограниченном прямолинейной границей с постоянным напором (граница I рода). В этом случае реальную скважину от­ражают от границы, получая фиктивный неограниченный пласт. Затем мето­дом суперпозиции решают задачу для двух симметрично расположенных скважин с дебитами, имеющими противоположные знаки. Если граница не­проницаемая (граница II рода), то у реальной и фиктивной скважин стоки имеют одинаковый знак.

Используя уравнения (5.9-5.11) и принципы суперпозиции (наложение течений) и зеркальных отражений можно решать фильтрационные задачи в любых ограниченных фильтрационных полях, каждый раз приводя реальную схему к фиктивным неограниченным условиям.

Широко используется в горном деле расчет водопритоков к выработкам по т.н. методу «большого колодца». В этом случае понижения уровня и водо-притоки (суммарные) рассчитываются по тем же формулам. Однако, радиус (т.н.приведенный) радиального потока принимается эквивалентным сумме отдельных радиальных потоков. Например, если скважины расположены в виде линейного ряда, то за приведенный радиус «большого колодца» может бытьпринят 0,21 (где l - протяженность линейного ряда), при площадном размещении скважин за радиус «большого колодца» принимают 0,16 П (где П - периметр площади размещения скважин).

В последние годы большое распространение получил метод расчета процессов фильтрации с использованием математического моделирования на ЭВМ (численное моделирование). Последний при наличии надежной гидро­геологической информации (начальные и граничные условия) позволяет дос­тигать универсальных результатов.

При выборе расчетных формул для оценки водопритоков в горные вы­работки и дренажные сооружения аналитическим методом необходимо знать (по данным геологоразведочного процесса или наблюдениям при эксплуата­ции) начальные и граничные условия: положение уровней (напоров), пара­метры водоносного горизонта (комплекса), условия питания и разгрузки под­земных вод (расчетные гидродинамические схемы).

Для определения водопритоков к горным выработкам и дренажным со­оружениям аналитическим методом обычно используют усредненные пара­метры водоносных горизонтов, приведенные к схеме однородного в разрезе и плане пласта.

Прогноз водопритоков к вертикальным и горизонтальным горным вы­работкам (шахтному стволу, карьеру, горизонтальным дренам) обычно про­водят раздельно для каждого вскрытого водоносного горизонта по методу «большого колодца», а затем рассматривают общий водоприток как сумму водопритоков из всех водоносных горизонтов.

Расчет водопритоков к вертикальным горным выработкам.

В условиях установившейся фильтрации приток к шахтному стволу, вскрывающему безнапорный водоносный пласт на всю мощность, при распо­ложении шахты у контура питания (река, водохранилище и т.д.), определяют по формуле (рис.5.):

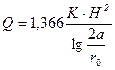(5.13)

где Q - водоприток к шахтному стволу, м³/сут; К - коэффициент фильтрации, м/сут; Н - мощность водоносного горизонта, м; r₀ - радиус шахтного ствола, м; а - расстояние от шахты до контура питания, м.

При нестационарной фильтрации для неограниченного в плане водо­носного горизонта водоприток к шахтному стволу можно рассчитать по формулам:

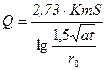(для напорной фильтрации).............. (5. 14)

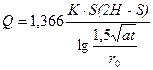(для безнапорной фильтрации)..….. (5.15)

где m - мощность водоносного горизонта, м; S - заданное понижения уровня, м; а - коэффициент пьезопроводности или уровнепроводности, м²/сут;

t - вре­мя сооружения выработки, сут.

Date: 2015-06-06; view: 4543; Нарушение авторских прав