
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема: Интеграл и его приложения
|
|
По данной теме сначала изучите § 45-52 гл.8,9 [l]. Затем ознакомьтесь с методическими указаниями по данной теме и внимательно разберите решение примеров из данного пособия. Решите задачи № 11-13, приведенные в пособии.
Неопределенный интеграл. Дифференцирование - это действие, с помощью которого по данной функции находится ее производная. Интегрирование - это действие, обратное дифференцированию. С помощью интегрирования по данной производной находится сама функция. Например, если
F/(x) =7x6, то F(x) = х7 так как (х7)/ = 7x6.
Дифференцируемая функция F(x), х  (а;b) называется первообразной для функции f(x) на интервале (a;b), если F'(x) = f(x) для каждого х
(а;b) называется первообразной для функции f(x) на интервале (a;b), если F'(x) = f(x) для каждого х  (а;b).
(а;b).
Совокупность всех первообразных функций f(x) на интервале (а;b) называют неопределенным интегралом от функции f(x) на этом интервале и пишут  =F(x) + C. Здесь f(x)dx - подынтегральное выражение; f(x) -подынтегральная функция; х - переменная интегрирования; С - произвольная постоянная.
=F(x) + C. Здесь f(x)dx - подынтегральное выражение; f(x) -подынтегральная функция; х - переменная интегрирования; С - произвольная постоянная.
Например,  , так как
, так как 
Приведем основные свойства неопределенного интеграла.
1. Дифференциал неопределенного интеграла равен подынтегральному
выражению:
d  dx=f(x)dx.
dx=f(x)dx.
2. Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной, т. е.
 df(x) = F(x) + C.
df(x) = F(x) + C.
3. Постоянный множитель можно выносить за знак неопределенного интеграла:
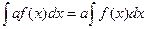
4. Неопределенный интеграл от алгебраической суммы функций равен
алгебраической сумме неопределенных интегралов от каждой функции:



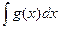
Основные формулы интегрирования (табличные интегралы)
1.  2.
2.  3.
3.  4.
4.  5.
5. 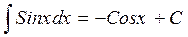 6.
6.  7.
7.  8.
8.  9.
9.  10.
10.  11.
11. 
| 12.  13.
13.   14
14  15.
15.  16.
16.  17.
17.  18.
18.  19.
19.  20.
20. 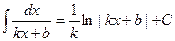 21.
21. 
|
Методы интегрирования:
Непосредственное интегрирование. Непосредственное интегрирование основано на прямом использовании свойств неопределенного интеграла и табличных интегралов.
Пример 1. Найти  .
.
Решение. Имеем,
 =
= 
 +
+  +
+ 

Метод подстановки. Сущность интегрирования методом подстановки заключается в преобразовании интеграла  в интеграл
в интеграл  F(t)dt, который легко вычисляется по какой-либо из основных формул интегрирования.
F(t)dt, который легко вычисляется по какой-либо из основных формул интегрирования.
Пример 2. Найти  .
.
Решение. Произведем подстановку 2-3x2 = t; тогда dt = - 6xdx, xdx= 
Далее получаем,

Определенный интеграл. Непосредственное вычисление определенного интеграла производится по формуле Ньютона-Лейбница:  = F(x)
= F(x)  = F(b)-F(a), где а - нижний предел, b - верхний предел, F(x) - какая-нибудь первообразная функции f(x).
= F(b)-F(a), где а - нижний предел, b - верхний предел, F(x) - какая-нибудь первообразная функции f(x).
Из этой формулы виден порядок вычисления определенного интеграла:
1) Находят одну из первообразных F(x) данной функции;
2) находят значения F(x) при х = а и х = b
3) вычисляют разность F(b) - F(a).
Приведем основные свойства определенного интеграла.
1. При перестановке пределов интеграла знак интеграла меняется на противоположный:  =-
=- 
2. Отрезок интегрирования можно разбивать на части:
 =
=  +
+ 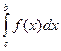
3. Постоянный множитель можно выносить за знак интеграла:  = c
= c 
4.Интеграл от суммы функций равен сумме интегралов от всех слагаемых:  =
= 


Методы интегрирования определенного интеграла (Те же что и для неопределенного интеграла):
1. Непосредственное интегрирование.
Пример 1. Вычислить интеграл 
Решение. Воспользуемся определением степени с дробным и отрицательным показателем и вычислим определенный интеграл:


 3
3 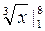 =
=
3 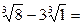 3 (2 - 1) = 3
3 (2 - 1) = 3
Пример 2. Вычислить интеграл 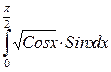
Решение. 1) Положим cos х = t; тогда t = -sin xdx и sin xdx = - dt.
2) Определим пределы интегрирования для переменной t: tн = Сos0 = 1; tв = Сos  = 0.
= 0.
3) Выразив подынтегральное выражение через t и dt и, перейдя к новым
пределам, получим
 =
=  =-
=-  .
.
Приложения определенного интеграла. Площадь плоской фигуры. Площадь криволинейной трапеции аАВb, ограниченной графиком непрерывной функции у = f(x), отрезком [а;b] оси Ох, отрезками прямых х = а и х = b, вычисляется по формуле S =  .
.
Площадь фигуры ABCD, ограниченной графиками непрерывных функций у =f(x) и у = g(x), где x  [a;b], отрезками прямых х = а и х = b, вычисляется по формуле
[a;b], отрезками прямых х = а и х = b, вычисляется по формуле
S = 
Пример 3. Вычислить площадь фигуры, ограниченной линиями у = x2 и у2 х.
Решение. Найдем пределы интегрирования, т. е. абсциссы точек пересечения графиков функций у = х2 и у2 = х. Для этого решим систему
 х4 = х, х(х3 –1) = 0, х = 0 и х = 1.
х4 = х, х(х3 –1) = 0, х = 0 и х = 1.
Искомую площадь вычисляем по формуле S =  при f(x) = х2, g(x)=
при f(x) = х2, g(x)=  : S =
: S =  =
= 
Date: 2015-11-15; view: 868; Нарушение авторских прав