
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры решения задач. Пример №1.Два когерентных источника S1и S2испускают свет с длиной волны λ=500 нм
|
|
Пример №1. Два когерентных источника S 1и S 2испускают свет с длиной волны λ= 500 нм. На каком расстоянии х от точки О на экране располагается первый максимум освещённости (k= 1), если расстояние между источниками d= 0,5мм, а расстояние от каждого источника до экрана L= 2м.
| d |
| S2 |
| S1 |
| экран |
| С |
| k=1 |
| r2 |
| r1 |
| d/2 |
| d/2 |
| L |
| k=0 |
| k=1 |
| M |
| х |
Пути лучей определим теоремой Пифагора:  и
и 
 (1)
(1)
 , (2)
, (2)
 , или
, или 
Интерференционная картина будет чёткой, если расстояние  между источниками невелико по сравнению с расстоянием их до экрана
между источниками невелико по сравнению с расстоянием их до экрана 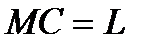 , т.к. d<<L. В этом случае
, т.к. d<<L. В этом случае  и
и  , или
, или  откуда
откуда  .
.
Согласно условию максимума освещённости при интерференции 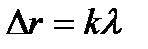 .
.
С учётом этого 
Пример №2. Расстояние между штрихами дифракционной решётки d= 3мм. На решётку падает нормально свет с длиной волны λ= 0,58мкм. Максимум какого наибольшего порядка падает на эту решётку?
Решение:
На основании формулы дифракционной решётки напишем выражение порядка дифракционного максимума:
 (1)
(1)
где d – период решётки; φ – угол между направлением на дифракционный максимум и нормалью к решётке; λ – длина волны монохроматического света.
Так как sin φ не может быть больше 1, то число т не может быть больше  , т.е.
, т.е.
 (2)
(2)
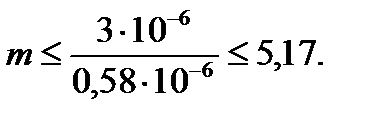
Если учесть, что порядок максимумов является целым числом, то т max =5.
Пример №3. Пучок естественного света падает на полированную поверхность стеклянной пластинки, погружённой в жидкость. Отражённый от пластины пучок света составляет угол  с падающим пучком. Определить показатель преломления п жидкости, если отражённый свет полностью поляризован.
с падающим пучком. Определить показатель преломления п жидкости, если отражённый свет полностью поляризован.
Решение:
Согласно закону Брюстера, свет, отражённый от диэлектрика, полностью поляризован в том случае, если тангенс угла падения
 ,
,
где п 21 – относительный показатель преломления второй среды (стекла) относительно первой (жидкости). Относительный показатель преломления равен отношению абсолютных показателей преломления этих сред.
| п1 |
| п2 |
| ε2 |
| ε1 ε1 |
Следовательно, 
Согласно условию задачи, отражённый луч повёрнут на угол φ относительно падающего луча. Так как угол падения равен углу отражения, то  и, следовательно,
и, следовательно,  , откуда
, откуда  .
.
Подставим числовые значения:
 .
.
Пример №4. Максимумэнергии излучения чёрного тела при некоторой температуре приходится на длину волны  . Вычислить излучённость тела при этой температуре и энергию W, излучаемую с площади
. Вычислить излучённость тела при этой температуре и энергию W, излучаемую с площади 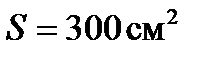 поверхности тела за время
поверхности тела за время  . Определить также массу, соответствующую этой энергии.
. Определить также массу, соответствующую этой энергии.
Решение:
Излучённость чёрного тела определим из закона Стефана-Больцмана:
 , (1)
, (1)
где σ – постоянная Стефана-Больцмана;
Т – термодинамическая температура тела.
Из закона смещения Вина 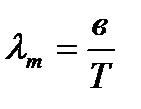 определим
определим
 , (2)
, (2)
где λт – длина волны, на которую приходится максимум излучения при температуре Т; в – постоянная Вина.
Подставив выражение для Т из (2) в (1), получим:
 . (3)
. (3)
Энергию, излучаемую с площади S поверхности тела за время t, определим по формуле
 . (4)
. (4)
По закону Эйнштейна взаимосвязи энергии и массы
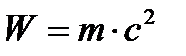 .
.
Найдём массу, соответствующую энергии излучателя:
 . (5)
. (5)
Проверим размерность (3):
 .
.
Подставим числовые значения величин в формулы (3), (4), (5) и вычислим:

Пример №5. Определить импульс Р и кинетическую энергию Т частицы, движущейся со скоростью  , где с – скорость света в вакууме.
, где с – скорость света в вакууме.
Решение:
Импульсом частицы называется произведение массы частицы на её скорость:
 . (1)
. (1)
Так как скорость электрона близка к скорости света, то необходимо учесть зависимость массы от скорости, определяемую по формуле
 , (2)
, (2)
где т – масса движущейся частицы; т 0 – масса покоящейся частицы; 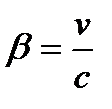 − скорость частицы, выражаемая в долях скорости света.
− скорость частицы, выражаемая в долях скорости света.
Заменив в формуле (1) массу т её выражением (2) и приняв во внимание, что  , получим выражение для релятивистского импульса:
, получим выражение для релятивистского импульса:
 . (3)
. (3)
Подставим числовые значения величин, входящих в формулу (3):
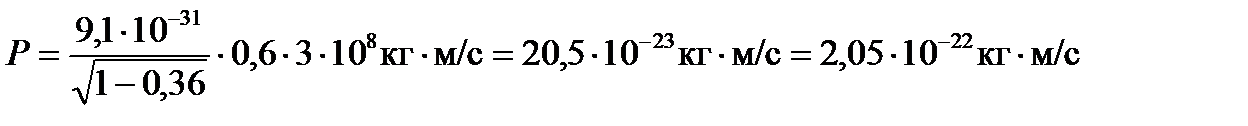 .
.
В релятивистской механике кинетическая энергия Т частицы определяется как разность между полной энергией Е и энергией покоя Е 0 этой частицы, т.е.  . Так как
. Так как  , то
, то  . Учитывая зависимость массы от скорости, получим:
. Учитывая зависимость массы от скорости, получим:
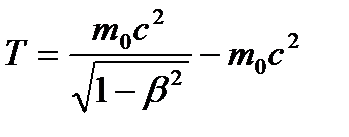 ,
,
или  . (4)
. (4)
Подставив числовые данные, выраженные в единицах СИ, найдём:
 .
.
Во внесистемных единицах энергия покоя электрона  .
.
Подставив это выражение в формулу (4), получим:
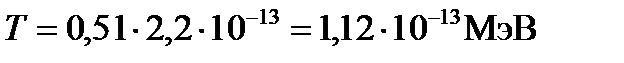 .
.
Пример №6. Определить скорость v электрона, имеющего кинетическую энергию 
Решение:
В релятивистской механике кинетическая энергия Т частицы определяется как разность между полной энергией Е и энергией покоя Е 0 этой частицы, т.е.  . Так как
. Так как  и
и 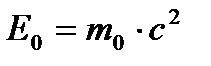 , то, учитывая зависимость массы от скорости, получим:
, то, учитывая зависимость массы от скорости, получим:
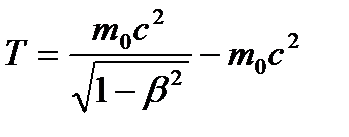 , (1)
, (1)
где т0 – масса покоящейся частицы.
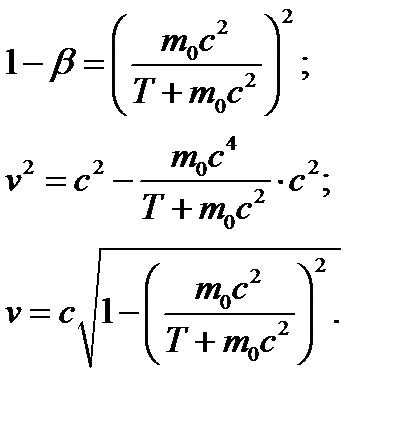 (2)
(2)
Во внесистемных единицах энергия покоя равна  .
.
Подставив числовые значения, найдём:
 .
.
Пример №7. Длина волны, на которую приходится максимум энергии излучения абсолютно чёрного тела,  . Определить температуру Т тела.
. Определить температуру Т тела.
Решение:
Температуру Т можно вычислить с помощью закона смещения Вина:
 , (1)
, (1)
где в – постоянная закона смещения Вина.
Используя формулу (1), получим:
 . (2)
. (2)
Выпишем числовые значения величин, входящих в эту формулу:

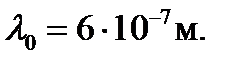
Подставим числовые значения в формулу (2), произведём вычисления:

Пример №8. На цинковую пластину падает пучок ультрафиолетовых лучей ( ). Определить максимальную кинетическую энергию
). Определить максимальную кинетическую энергию  и максимальную скорость
и максимальную скорость  фотоэлектронов.
фотоэлектронов.
Решение:
Максимальную скорость фотоэлектронов можно определить из уравнения Эйнштейна для фотоэффекта:
 (1)
(1)
где Е – энергия фотонов, падающих на поверхность металла; А – работа выхода; Ттах – максимальная кинетическая энергия фотоэлектронов.
Энергия фотона вычисляется также по формуле
 (2)
(2)
где h – постоянная Планка; с – скорость света в вакууме; l - длина волны.
Кинетическая энергия электрона может быть выражена или по классической формуле
 (3)
(3)
или по релятивистской формуле
 (4)
(4)
в зависимости от того, какая скорость сообщается фотоэлектрону.
Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект. Если энергия Е фотона много меньше энергии покоя Е0 электрона, то может быть применена формула (3), если же Е сравнима по величине с Е0, то вычисление по формуле (3) приводит к ошибке, поэтому нужно пользоваться формулой (4).
1. Вычислим энергию фотона ультрафиолетовых лучей по формуле (2):
 ,
,
или

Полученная энергия фотона (6,22 эВ) много меньше энергии покоя электрона(0,51 МэВ). Следовательно, для данного случая кинетическая энергия фотоэлектрона в формуле (1) может быть выражена по классической формуле (3):

откуда  (5)
(5)
Выпишем числовые значения величин:
E 1=9,945 ∙ 10-19Дж,
А = 4,7 эВ = 4,7 ∙ 1,6 ∙ 10-19Дж = 0,75 ∙ 10-18 Дж.
Подставив числовые значения в формулы (3) и (5), найдём:

Пример №9. Параллельный пучок монохроматических лучей с длиной волны  падает на зачернённую поверхность и производит на неё давление
падает на зачернённую поверхность и производит на неё давление 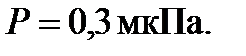 Определить концентрацию п фотонов в световом пучке.
Определить концентрацию п фотонов в световом пучке.
Решение:
Концентрация п фотонов в пучке может быть найдена как частное от деления объёмной плотности энергии  на энергию Е одного фотона:
на энергию Е одного фотона:
 (1)
(1)
Из формулы  определяющей давление света, где
определяющей давление света, где  - коэффициент отражения, найдём:
- коэффициент отражения, найдём:
 . (2)
. (2)
Подставив выражение для  из уравнения (2) в формулу (1), получим:
из уравнения (2) в формулу (1), получим:
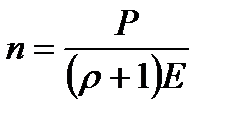 . (3)
. (3)
Энергия фотона зависит от частоты  , а следовательно, и от длины световой волны
, а следовательно, и от длины световой волны 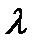 :
:
 . (4)
. (4)
Подставив выражение для энергии фотона в формулу (3), определим искомую концентрацию фотонов:
 (5)
(5)
Коэффициент отражения 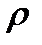 для зачернённой поверхности принимаем равным нулю.
для зачернённой поверхности принимаем равным нулю.
Подставив числовые значения в формулу (5), получим:

Date: 2015-11-15; view: 4404; Нарушение авторских прав