Уравнение динамики вращательного движения тверд.тела

Согласно уравнению второй закон Ньютона для вращательного движения

По определению угловое ускорение и тогда это уравнение можно

переписать следующим образом

с учетом

или

(5.10)

Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела , равно импульсу момента всех внешних сил, действующих на это тело.

Момент импульса материальной точки относительно точки O определяется векторным произведением
, где — радиус-вектор, проведенный из точки O, 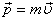— импульс материальной точки.
Момент импульса материальной точки относительно неподвижной оси равен проекции на эту ось вектора момента импульса, определенного относительно произвольной точки O данной оси. Значение момента импульса не зависит от положения точки O на оси z.

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что , получим
.

Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса):
.

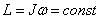Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело:
.

Величина момента импульса системы материальных то- чек, вообще говоря, зависит от выбора начала координат, относительно которого он определен. И только в том случае, если в выбранной систе- ме отсчета скорость поступательного движения твердого тела V = 0, его момент импульса не зависит от выбора точки отсчета. Поэтому в этом случае естественно в качестве такой точки выбрать центр инерции тела — начало подвижной системы координат. Тогда в выражении для момента импульса

M = Xm[r × v] (1) скорость v надо заменить на [Ω × r]: M = Xm [r × [Ω × r]] = Xm ¡ Ωr 2 − r(Ω · r) ¢. (2)

Вводя тензорные обозначения, получим Mi = Xm ¡ Ωix 2 l − xi(Ωkxk) ¢ = Xm(δikΩkx 2 l − xixkΩk) = = Ωk Xm(x 2 l δik − xixk) = ΩkIik. (3) Таким образом, связь между двумя векторами M и Ω можно записать в виде Mi = IikΩk. (4) Если оси x1, x2, x3 направлены вдоль главных осей инерции тела, то недиагональные компоненты тензора инерции равны нулю и эта формула дает M1 = I1Ω1, M2 = I2Ω2, M3 = I3Ω3.

Момент импульса материальной точки» Закон сохранения момента импульса Аналогично моменту силы определяется момент импульса (момент количества движения) материальной точки. Момент импульса относительно точки О равен

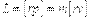
Введя плечо 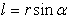, модуль вектора момента импульса можно записатьв виде:

(37.2)

Моментом импульса относительно оси z называется составляющая Lz по этой оси момента импульса L относительно точки О, лежащей на оси

Выясним, чем определяется изменение момента импульса со временем. Для этого продифференцируем (37.1) по времени t, воспользовавшись правилом дифференцирования произведения:

(37.5)

Первое слагаемое равно нулю, так как оно представляет собой векторное произведение векторов одинакового направления. В самом деле, вектор равен вектору скорости v и, следовательно, совпадает по направлению с вектором р=mv. Вектор 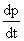по второму закону Ньютона равен действующей на тело силе f [см. (22.3)]. Следовательно, выражение (37.5) можно написать так:

(37.6)

где М — момент приложенных к материальной точке сил, взятый относительно той же точки О, относительно которой берется момент импульса L.

Из соотношения (37.6) следует, что если результирующий момент действующих на материальную точку сил относительно какой-либо точки О равен нулю, то момент импульса материальной точки, взятый относительно той же точки О будет оставаться постоянным.

Взяв составляющие по оси z от векторов, входящих в формулу (37.6), получим выражение[1]:

(37.7)

). Из сравнения этих формул вытекает, что подобно тому, как производная по времени от импульса равна силе, действующей на материальную точку, производная по времени от момента импульса равна моменту силы.

Рассмотрим несколько примеров.

огласно формуле (2.11)

где 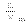—проекция на ось z вектора , а L_z- проекция на ось z вектора L. Умножим обе части равенства на орт e_z оси z и, учтя, что e_z от t не зависит, внесем его в правой части под знак производной. В результате получим:

Но произведение e_z на проекцию вектора на ось z дает составляющую этого вектора по оси z (см. сноску на стр. 132). Следовательно,

где — составляющая пo оси z вектора .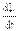

Date: 2015-11-15; view: 350; Нарушение авторских прав