Способы задания множеств

Обсудив особенности употребления логической символики, вернемся к рассмотрению множеств.

Два множества 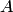и 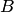считают равными, если любой элемент множества 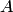является элементом множества 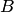и наоборот. Из приведенного определения равных множеств следует, что множество полностью определяется своими элементами.

Рассмотрим способы задания конкретных множеств. Для конечного множества, число элементов которого относительно невелико, может быть использован способ непосредственного перечисления элементов. Элементы конечного множества перечисляют в фигурных скобках в произвольном фиксированном порядке . Подчеркнем, что поскольку множество полностью определено своими элементами, то при задании конечного множества порядок, в котором перечислены его элементы, не имеет значения. Поэтому записи и т.д. все задают одно и то же множество. Кроме того, иногда в записи множеств используют повторения элементов. Будем считать, что запись задает то же самое множество, что и запись .

В общем случае для конечного множества используют форму записи . Как правило, при этом избегают повторений элементов. Тогда конечное множество, заданное записью , состоит из элементов. Его называют также n-элементным множеством.

Однако способ задания множества путем непосредственного перечисления его элементов применим в весьма узком диапазоне конечных множеств. Наиболее общим способом задания конкретных множеств является указание некоторого свойства, которым должны обладать все элементы описываемого множества, и только они.

Эта идея реализуется следующим образом. Пусть переменное пробегает некоторое множество , называемое универсальным множеством. Мы предполагаем, что рассматриваются только такие множества, элементы которых являются и элементами множества . В таком случае свойство, которым обладают исключительно элементы данного множества 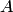, может быть выражено посредством предиката , выполняющегося тогда и только тогда, когда переменное принимает произвольное значение из множества 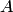. Иначе говоря, истинно тогда и только тогда, когда вместо подставляется индивидная константа .

Предикат называют в этом случае характеристическим предикатом множества 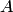, а свойство, выражаемое с помощью этого предиката, — характеристическим свойством или коллективизирующим свойством.

Множество, заданное через характеристический предикат, записывается в следующей форме:

Например, означает, что " 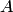есть множество, состоящее из всех таких элементов , что каждое из них есть четное натуральное число".

Термин "коллективизирующее свойство" мотивирован тем, что это свойство позволяет собрать разрозненные элементы в единое целое. Так, свойство, определяющее множество 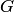(см. ниже), в буквальном смысле слова формирует некий "коллектив":

G = {х: х есть студент 2-го курса специальности ИУ5 МГТУ им. Баумана, поступивший в 1999 г.},

Если мы вернемся к канторовскому определению множества, то характеристический предикат множества и есть тот закон, посредством которого совокупность элементов соединяется в единое целое. Предикат, задающий коллективизирующее свойство, может быть тождественно ложным. Множество, определенное таким образом, не будет иметь ни одного элемента. Его называют пустым множеством и обозначают .

В противоположность этому тождественно истинный характеристический предикат задает универсальное множество.

Обратим внимание на то, что не каждый предикат выражает какое-то коллективизирующее свойство.

Замечание 1.1. Конкретное содержание понятия универсального множества определяется тем конкретным контекстом, в котором мы применяем теоретико-множественные идеи. Например, если мы занимаемся только различными числовыми множествами, то в качестве универсального может фигурировать множество всех действительных чисел. В каждом разделе математики рассматривается относительно ограниченный набор множеств. Поэтому удобно полагать, что элементы каждого из этих множеств суть также и элементы некоторого "объемлющего" их универсального множества. Зафиксировав универсальное множество, мы тем самым фиксируем область значений всех фигурирующих в наших математических рассуждениях переменных и констант. В этом случае как раз и можно не указывать в кванторах то множество, которое пробегает связываемое квантором переменное. В дальнейшем изложении мы встретимся с разными примерами конкретных универсальных множеств.

Date: 2015-11-15; view: 503; Нарушение авторских прав