Меры расстояния

Объединение или метод древовидной кластеризации используется при формировании кластеров несходства или расстояния между объектами. Эти расстояния могут определяться в одномерном или многомерном пространстве. Наиболее прямой путь вычисления расстояний между объектами в многомерном пространстве состоит в вычислении евклидовых расстояний. Если имеется двух- или трёхмерное пространство, то эта мера является реальным геометрическим расстоянием между объектами в пространстве (как будто расстояния между объектами измерены рулеткой). Однако алгоритм объединения не «заботится» о том, являются ли «предоставленные» для этого расстояния настоящими или некоторыми другими производными мерами расстояния, что более значимо для исследователя; и задачей исследователей является подобрать правильный метод для специфических применений.

Евклидово расстояние. Это, по-видимому, наиболее общий тип расстояния. Оно попросту является геометрическим расстоянием в многомерном пространстве и вычисляется следующим образом:

.

Заметим, что евклидово расстояние (и его квадрат) вычисляется по исходным, а не по стандартизованным данным. Это обычный способ его вычисления, который имеет определенные преимущества (например, расстояние между двумя объектами не изменяется при введении в анализ нового объекта, который может оказаться выбросом). Тем не менее, на расстояния могут сильно влиять различия между осями, по координатам которых вычисляются эти расстояния. К примеру, если одна из осей измерена в сантиметрах, а потом она переводится в миллиметры (значения умножаются на 10), то окончательное евклидово расстояние (или квадрат евклидова расстояния), вычисляемое по координатам, сильно изменится, и, как следствие, результаты кластерного анализа могут сильно отличаться от предыдущих.

Квадрат евклидова расстояния. Иногда может возникнуть желание возвести в квадрат стандартное евклидово расстояние, чтобы придать большие веса более отдаленным друг от друга объектам. Это расстояние вычисляется следующим образом (см. также замечания в предыдущем пункте):

.

Расстояние городских кварталов (манхэттенское расстояние). Это расстояние является просто средним разностей по координатам. В большинстве случаев эта мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида. Однако отметим, что для этой меры влияние отдельных больших разностей (выбросов) уменьшается (так как они не возводятся в квадрат). Манхэттенское расстояние вычисляется по формуле:

.

Расстояние Чебышева. Это расстояние может оказаться полезным, когда желают определить два объекта как «различные», если они различаются по какой-либо одной координате (каким-либо одним измерением). Расстояние Чебышева вычисляется по формуле:

.

Расстояние Махаланобиса. Данное расстояние учитывает корреляции между переменными.

.

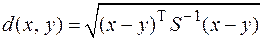Данная мера расстояния плохо работает, если ковариационная матрица S высчитывается на всем множестве входных данных. Вообще лучше не использовать расстояние Махаланобиса если есть структура (т. е. кластеры) – тем самым в S будут внесены искажения. В то же время, будучи сосредоточенной на конкретном классе (группе данных), т. е. внутри кластера, данная мера расстояния показывает хорошие результаты.

Степенное расстояние. Иногда желают прогрессивно увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Это может быть достигнуто с использованием степенного расстояния. Степенное расстояние вычисляется по формуле:

,

где r и p – параметры, определяемые пользователем. Параметр p ответственен за постепенное взвешивание разностей по отдельным координатам, параметр r ответственен за прогрессивное взвешивание больших расстояний между объектами. Если оба параметра – r и p, равны двум, то это расстояние совпадает с расстоянием Евклида.

Процент несогласия. Эта мера используется в тех случаях, когда данные являются категориальными. Это расстояние вычисляется по формуле:

.

Пиковое расстояние предполагает независимость между случайными переменными, что говорит о расстоянии в ортогональном пространстве. Но в практических приложениях эти переменные не являются независимыми. Это расстояние вычисляется по формуле:

.

Любую из приведенных мер расстояния можно выбирать с уверенностью лишь в том случае, если имеется информация о характере данных, подвергаемых кластеризации.

Date: 2015-11-15; view: 603; Нарушение авторских прав