Введение. Всякое тело, подвешенное в точке, лежащей выше его центра тяжести, может колебаться и представляет собой физический маятник (рис

Всякое тело, подвешенное в точке, лежащей выше его центра тяжести, может колебаться и представляет собой физический маятник (рис. 10.1).

Если мятник отклонить от положения равновесия на угол j, то сила тяжести создает относительно оси вращения (проходит через т. О₁ перпендикулярно к плоскости рисунка) вращающий момент

, (10.1)

где l₁ - расстояние от оси вращения до центра тяжести С, m – масса маятника, а угол j отсчитывается от вертикальной линии против часовой стрелки. Момент силы М стремится вернуть маятник в положение равновесия.

При малых углах отклонения колебания маятника будут близки к гармоническим. Действительно, при малых углах sinj» j и (10.1) принимает вид:

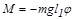. (10.2)

По основному закону динамики вращательного движения

, (10.3)

где J – момент инерции маятника относительно оси О₁,

ε = d²φ / dt² - угловое ускорение

Подставляем M и ε в (10.3), получим

. (10.4)

Обозначая , перепишем (10.4) в виде

. (10.5)

Уравнение (10.5) – дифференциальное уравнение гармонических колебаний. Решением этого уравнения является функция

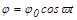, (10.6)

где j₀ - максимальный угол отклонения маятника от положения равновесия, а - круговая (или циклическая) частота.

Для периода колебаний получаем:

. (10.7)

Величину называют приведенной длиной физического маятника. Подставив это в (10.7), найдем, что приведенной длина физического маятника равна длине математического маятника с таким же периодом колебаний.

Точка, находящаяся на расстоянии l_пр от точки подвеса по лини, проходящей через центр тяжести, называется центром качания.

Точка подвеса и центр качания обладают свойством обратимости: если центр качания сделать точкой подвеса, то прежняя точка подвеса станет новым центром качания, при этом период колебаний не изменится.

Для доказательства этого утверждения воспользуемся теоремой Штейнера: момент инерции тела относительно оси z равен моменту инерции этого тела относительно оси z’, проходящей через его центр инерции параллельно оси z, плюс произведение массы тела на квадрат расстояния между осями z и z’, т.е. (рис. 10.2)

, (10.8)

где J - момент инерции относительно оси z, J₀ - момент инерции относительно оси z’, m - масса тела, l - расстояние между осями z и z’.

Рассмотрим вращение физического маятника вокруг т. О₁ (рис. 10.1).

Проведем линию О₁С и на ее продолжении возьмем точку О₂, такую, что О₁О₂= . Обозначим О₂С= , так что . Тогда

.Таким образом, . Теперь перевернем маятник и рассмотрим его вращение вокруг оси, проходящей через т. О₂, при этом

,

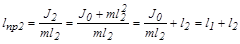откуда следует, что l_пр1 =l_пр2.

Зная период колебаний физического маятника и его приведенную длину l_пр, ускорение свободного падения рассчитаем по формуле:

. (10.9)

Таким образом, для определения g с помощью физического маятника необходимо измерить период колебаний T и определить приведенную длину маятника l_пр.

Date: 2015-11-13; view: 414; Нарушение авторских прав