Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Нормальные формы для формул алгебры высказываний
|
|
Для каждой формулы алгебры высказываний можно указать равносильную ей формулу, содержащую лишь отрицание, конъюнкцию и дизъюнкцию. Для этого нужно, все имеющиеся в формуле импликации и эквивалентности выразить через отрицание, конъюнкцию и дизъюнкцию.
Понятие нормальных форм.
Конъюнктивным одночленом от переменных x1, x2,…, xn называется конъюнкция этих переменных или их отрицаний (в конъюнктивный одночлен может входить и переменная, и ее отрицание одновременно).
Например: 
.
Дизъюнктивным одночленом от переменных x1, x2,…, xn называется дизъюнкция этих переменных или их отрицаний (в дизъюнктивный одночлен может входить и переменная, и ее отрицание одновременно).
Например: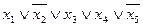 
.
Дизъюнктивной нормальной формой называется дизъюнкция конъюнктивных одночленов 
, где ki (i = 1,2,…,s) – являются конъюнктивными одночленами (не обязательно разными).
Конъюнктивной нормальной формой называется конъюнкция дизъюнктивных одночленов 
, где di (i = 1,2,…,p) – являются дизъюнктивными одночленами (не обязательно разными).
Дизъюнктивной (конъюнктивной) нормальной формой будут называться выражения при s = 1 и p = 1.
Нормальную форму, равносильную форме F называют просто нормальной формой этой формулы.
Всякая формула обладает как дизъюнктивной нормальной формой, так и конъюнктивной нормальной формой. У этой формулы F существует неограниченно много дизъюнктивных и конъюнктивных нормальных форм. Среди них существует уникальная совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ).
Одночлен (конъюнктивный или дизъюнктивный) от переменных высказываний 
называется совершенным, если в него от каждой пары Аi 
(i = 1,2,….n) входит точно одна буква.
Нормальная форма (конъюнктивная или дизъюнктивная) от переменных высказываний называется совершенной, если в нее входят лишь совершенные одночлены соответственно .
Теорема (о представлении формул алгебры высказываний СДНФ).
Каждая не тождественно ложная формула алгебры высказываний от n аргументов имеет единственную совершенную дизъюнктивную нормальную форму.
Правила отыскания СДНФ:
1. Выбирают все наборы значений переменных, на которых формула принимает значение 1;
2. Для каждого набора выписывают совершенный конъюнктивный одночлен, принимающий значение 1 на этом наборе и только на нем.
3. Полученные совершенные конъюнктивные одночлены соединить знаками дизъюнкции.
Теорема (о представлении формул алгебры высказываний СКНФ).
Каждая формула алгебры высказываний от n аргументов, не являющаяся тавтологией, имеет единственную совершенную конъюнктивную нормальную форму.
Правила отыскания СКНФ:
1. Выбирают все наборы значений переменных, на которых формула принимает значение 0;
2. Для каждого набора выписывают совершенный дизъюнктивный одночлен, принимающий значение 0 на этом наборе и только на нем.
3. Полученные совершенные дизъюнктивные одночлены соединить знаками конъюнкции.
Date: 2015-11-13; view: 1322; Нарушение авторских прав