Шестое действие

Сложение и умножение имеют по одному обратному действию, которые называются вычитанием и делением. Пятое математическое действие – возведение в степень – имеет два обратных: разыскание основания и разыскание показателя. Разыскание основания есть шестое математическое действие и называется извлечением корня. Нахождение показателя – седьмое действие – называется логарифмированием. Причину того, что возведение в степень имеет два обратных действия, в то время как сложение и умножение – только по одному, понять нетрудно: оба слагаемых (первое и второе) равноправны, их можно поменять местами; то же верно относительно умножения; однако числа, участвующие в возведении в степень, т. е. основание и показатель степени, неравноправны между собой; переставить их, вообще говоря, нельзя (например, 3⁵ ¹ 5³). Поэтому разыскание каждого из чисел, участвующих в сложении и умножении, производится одинаковыми приемами, а разыскание основания степени и показателя степени выполняется различным образом.

Шестое действие, извлечение корня, обозначается знаком 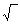. Не все знают, что это – видоизменение латинской буквы r, начальной в латинском слове, означающем "корень". Было время (XVI в.), когда знаком корня служила не строчная, а прописная буква R, а рядом с ней ставилась первая буква латинских слов "квадратный" (q) или "кубический" (с), чтобы указать, какой именно корень, требуется извлечь. [В учебнике математики Магницкого, по которому обучались у нас в течение всей первой половины XVIII в., вовсе нет особого знака для действия извлечения корня.] Например, писали

R. q. 4352

вместо нынешнего обозначения

.

Если прибавить к этому, что в ту эпоху еще не вошли в общее употребление, нынешние знаки для плюса и минуса, а вместо них писали буквы р. и т., и что наши скобки заменяли знаками |_ _|, то станет ясно, какой необычный для современного глаза вид должны были иметь тогда алгебраические выражения.

Вот пример из книги старинного математика Бомбелли (1572):

R. c. |_ R. q. 4352 p. 6 _| m. R. c. |_ R. q. 4352 m. 16 _|.

Мы написали бы то же самое иными знаками:

.

Кроме обозначения теперь употребляется для того же действия еще и другое, , весьма удобное в смысле обобщения: оно наглядно подчеркивает, что каждый корень есть не что иное, как степень, показатель которой – дробное число. Оно предложено было замечательным голландским математиком XVI в. Стевином.

<Paaaa

Date: 2015-11-13; view: 420; Нарушение авторских прав