
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

II.4. Географические координаты
|
|
Положение точек на земной поверхности определяется географической долготой и географической широтой.
В сетке географических координат через полюса Земли проводят большие круги — географические меридианы, а параллельно плоскости земного экватора — малые круги, называемые географическими параллелями. За начальный или нулевой принят Гринвичский меридиан, на котором находится астрономическая обсерватория вблизи Лондона.
Географическая долгота X отсчитывается вдоль экватора к востоку от Гринвичского меридиана со знаком "+" и к западу — со
знаком "-". Географическая широта у читывается вдоль меридианов в направлении географических полюсов со знаком "+" к северу и со знаком"-" к югу от экватора.
Географическая широта принимает значения от -90 до +90" а долгота — от -180 до +180° (рис. 11.13). Иногда географическую долготу измеряют в единицах времени от 0 до 24 часов, причем отсчитывают ее только в одном направлении — к востоку от Гринвича. Перевод угловых единиц в единицы времени проводят из расчета: 360° = 24 часа; 1 градус =4 минуты; 1мин= 4 секунды; 1 час - 15°; 1 минута= 15'; 1 секунда - 15".

|

|
Ш. СТРОЕНИЕ СОЛНЕЧНОЙ СИСТЕМЫ
Наша Земля вместе с другими планетами вращается вокруг Сол-нца. Ближайшая к Солнцу планета — Меркурий. Далее, по мере удаления от Солнца, следуют Венера, Земля, Марс, Юпитер, Сатурн Уран, Нептун, Плутон. Орбиты этих планет лежат вблизи одной плоскости, называемой плоскостью эклиптики.
Кроме планет, Солнечная система включает тысячи астероидом иногда называемых малыми планетами, множество комет и миллионы метеорных и метеоритных тел. Астероиды — это твердые глыбы неправильной формы. (Лишь у четырех самых крупных форма близка к щарообразной). Большинство из них движутся вокруг Сол-нца между орбитами Марса и Юпитера, образуя пояс астероидов.
По своим физическим характеристикам планеты Солнечной системы делятся на две группы. Планеты, расположенные между Солнцем и поясом астероидов — Меркурий, Венера, Земля, Марс,- земная группа планет. Они невелики по размерам и массе, имею-твердую поверхность и довольно высокую плотность и, кроме Мер курия, обладают атмосферами. Планеты, движущиеся за кольцом астероидов, образуют группу планет-гигантов: Сатурн, Уран, Не-птун. Они представляют собой газообразные тела, сжатые пол гигантским давлением. Данные о последней обнаруженной к сегод-няшнему дню планете — Плутоне — неполны.
Все планеты, включая Землю, обращаются вокруг Солнца и одном направлении, которое мы будем называть прямым (рис. III.1 масштабы искажены).
Размеры планетной системы огромны. Ее диаметр около 12 млрд км, а самая удаленная планета Плутон отстоит от Солнца в 40 paз
дальше, чем земля, Относительные средние расстояния планет от Солнца и периоды их обращения представлены в табл. III. 1.
Великий математик и астроном Иоганн Кеплер вывел законы, описывающие орбитальное движение планет:
1. 
 Планеты в своем движении вокруг Солнца описывают эллипс, причем Солнце находится в одном из фокусов этого эллипса.
Планеты в своем движении вокруг Солнца описывают эллипс, причем Солнце находится в одном из фокусов этого эллипса.
2. Прямая линия, соединяющая планету с Солнцем, так называемый радиус-вектор планеты, описывает равные площади в равные промежутки времени. Следствие из этого закона — непостоянство скорости движения планет по орбите.
3. Квадраты периодов обращения любых двух планет соотносятся между собой как кубы их средних расстояний от Солнца.
III. 1. Относительные средние расстояния планет от Солнца и периоды их обращения
| Планеты | R (большие полуоси орбит) | Т (периоды обращения планет) | |
| в относительных единицах | в абсолютных единицах | ||
| Меркурий | 0,387 | 0,241 | 87,97 суток |
| Венера | 0,723 | 0,615 | 224,70 суток |
| Земля | 1,000 | 1,000 | 365,26 суток |
| Марс | 1,524 | 1,881 | 1 год 322 дня |
| Юпитер | 5,203 | 11,862 | 11 лет 315 дней |
| Сатурн | 9,539 | 29,458 | 29 лет 167 дней |
| Уран | 19,191 | - | 84 года 8 дней |
| Нептун | 30,061 | - | 164 года 282 дня |
| Плутон | 39,44-39,529 | - | 247 лет 305 дней |

Орбиты всех планет имеют один общий фокус, находящийся в центре Солнца (рис. Ш.2). Эллиптическую форму имеет и орбита Луны — спутника Земли. В одном из фокусов этого эллипса находится Земля (рис. Ш.З).
|
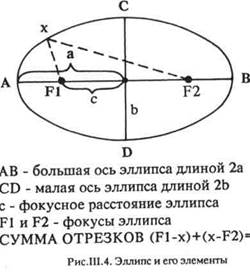
Можно нестрого
определить эллипс как сплюснутую окружность, но лучше воспользоваться математическим определением: эллипс — это плоская замкнутая кривая, для любой точки которой сумма расстояний от двух фокусов постоянна и v равна длине большой оси эллипса (рис. Ш.4).
Степень вытя-нутости эллипса характеризуется эксцентриситетом е - с/а.
Значение эксцентриситета меняется от 0 до 1. При е - 0 эллипс превращается в окружность, а при е- 1 — в разомкнутую кривую — параболу, имеющую лишь один фокус.
Все планеты Солнечной системы, кроме Меркурия и Плутона, имеют маленькие эксцентриситеты, т.е. движутся по орбитам, близким к правильным окружностям. Орбиты самой ближней к Солнцу и самой удаленной от него планет более вытянуты (см. табл. III.2).
Данные таблицы показывают, что наиболее близкие к окружности орбиты имеют Венера и Нептун. Еще древние астрономы и астрологи знали, что планеты, перемещаясь по звездному небу

|

|
111,2. Эксцентриситеты и наклон орбит планет Солнечной системы
| Планеты | Эксцентриситеты орбит | Наклон орбит | |
| градусы | минуты | ||
| Меркурий | 0,206 | ||
| Венера | 0,007 | ||
| Земля | 0,017 | - | - |
| 1 Марс | 0,093 | ||
| Юпитер | 0,048 | ||
| . Сатурн | 0,056 | ||
| Уран | 0,046 | ||
| Нептун | 0,009 | ||
| Плутон | 0,249 | 9_________ | |
вблизи эклиптики, периодически удаляются от нее в обе стороны на небольшие угловые расстояния, например, Юпитер — на Г, Марс — на 2, Сатурн — на 2,5, Меркурий — на 7°. Эти удаления планет объясняются наклонением плоскостей их орбит к плоскости земной орбиты, т.е. плоскости эклиптики. Величины наклона орбит планет I представлены в табл. Ш.2, откуда видно, что наиболее приближена I к плоскости эклиптики плоскость орбиты Урана, а наиболее удалены плоскости орбит Меркурия и Плутона.
Прямая линия, по которойплоскость орбиты планеты (любой, кроме Земли, чья плоскость орбиты и является плоскостью эклиптики) пересекается с плоскостью эклиптики, называется линией узлов орбиты, а точки ее пересечения с эклиптикой — узлами орбиты данной планеты.
В восходящем узле планета переходит к северу от эклиптики, а в нисходящем — к югу от нее (рис. III.5). Поэтому
восходящий узел
иногда называют
северным, а
нисходящий - южным.
Вернемся к
рассмотрению
второго закона
Кеплера. Ближай
шая к Солнцу точ-
ка орбиты
называется перигелием 1, а наиболее удаленная — афелием.. Эти точки лежат на большой оси
орбиты по разные стороны от солн-ца (рис. Ш.6). Большая ось орбиты носит название линии апсид. При движении планеты вокруг Солнца ее гелиоцентрическое расстояние (радиус-вектор) постоянно изменяется. Несложно показать, что длина радиус-вектора при нахождении планеты в точке перигелия равна а(1 — е), в точке афелия а(1 + е), где а — длина большой полуоси
1 "пери" (греч.) — около.
2 Искаженное "апогелий", где "а п о" (греч.) — вдали.
 |
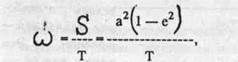
|
эллиптической орбиты, равная среднему расстоянию планеты от Солнца.
На рис. III.6 площади секторов S1 и S2 равны. В соответствии со вторым законом Кеплера вблизи перигелия планета имеет максимальную скорость обращения вокруг Солнца, а вблизи афелия — минимальную. Площадь, описываемая радиус-вектором планеты в единицу времени, называется ее секториальной скоростью. Второй закон Кеплера иногда формулируют и так: секториаль-ная скорость планеты есть величина постоянная.
Секториальная скорость планеты связана с периодом ее обращения вокруг Солнца (сидерическим, или звездным периодом) формулой:
где W— секториальная скорость планеты; S— площадь ее орбиты; Т — сидерический период обращения; а — большая полуось орбиты; е — эксцентриситет.
Первые два закона Кеплера описывают планетарные орбиты по отдельности, а третий связывает все планеты в единую систему.
Если через Тп обозначить сидерический период обращения п-ой планеты, а через ап — ее среднее гелиоцентрическое расстояние (большую полуось орбиты планеты), то

По известным периодам обращения небесных тел вокруг Солнца несложно вычислить их средние расстояния от него в относительных единицах (см. табл. III. 1).
Кроме поступательного движения планет по их эллиптическим орбитам вокруг Солнца каждая из планет, включая Землю и Луну, вращается вокруг своей собственной оси. Меркурий медленно вращается вокруг оси вращения в том же направлении, что и Земля (далее будем говорить "в прямом направлении") с периодом 58,65 земных суток, что составляет примерно 2/3 периода его обращения вокруг Солнца* Наклон оси вращения Меркурия к плоскости его орбиты равен 7°.
Ось вращения Венеры отклонена от перпендикуляра на 3°. Планета вращается вокруг своей оси в направлении, обратном направлению вращения Земли. Вращение Марса прямое с периодом 24 часа 37 минут и 23 секунды. Наклон оси вращения Марса (24е 48') близок к наклону земной оси (23°27'). Ось вращения Юпитера отклонена от перпендикуляра к плоскости его орбиты на 3°7\ Газообразное состояние Юпитера определяет его зональное вращение. Экваториальная зона вращается с периодом 9 часов 50,5 минут, а умеренные зоны — несколько медленнее — 9 часов 55,7 минут. Быстрым
| Ш.З. Периоды вращения планет и наклон их осей вращения относительно вертикали к плоскости эклиптики | ||
| Планеты | Период вращения | Наклон оси вращения |
| Меркурий | 58,65 дней (земных) | 7град |
| Венера | -243,16 дней | 177град |
| Земля | 23 часа 56 минут | 23e27' |
| Марс | 24 часа 37 минут | 24в48, |
| Юпитер | 9 часов 50 минут | 3 град 7 мин |
| Сатурн | 10 часов 14 минут | 26°45' |
| Уран | -10 часов 49 минут | 98° |
| Нептун | 15 часов 48 минут | |
| Плутон | 6 дней 9 часов 17 минут | ? |
*3нак минус означает, что планета вращается вокруг своей направлении, обратном направлению вращения Земли.
вращением Юпитера объясняется его значительное сжатие у полюсов.
У Сатурна ось вращения наклонена под углом 26°45\ а вращается он подобно Юпитеру зонально и очень быстро. Период вращения в экваториальной зоне составляет 10 часов 14 минут, а умеренных зон — 10 часов 38 минут.
Уран вращается в обратном направлении вокруг оси, отклоненной от перпендикуляра к плоскости его орбиты на 98°, т.е. его ось вращения лежит почти в плоскости его орбиты. Период вращения Урана вокруг оси — 10 часов 49 минут.
Нептун вращается в прямом направлении с периодом 15 часов 48 минут вокруг оси, наклоненной на 29°. Период вращения Плутона вокруг своей оси 6 дней 9 часов 17 минут. Угол наклона оси окончательна не установлен. Данные по периодам вращения планет и наклону осей вращения сведены в табл. III.3.
III.1. Сведения об орбитах и физических характеристиках планет
В табл. III.4 приведены параметры планетарных орбит. Буквенные обозначения расшифровываются следующим образом: а — большая полуось орбиты; е — эксцентриситет орбиты; i — наклонение орбиты (угол между плоскостью орбиты и плоскостью эклиптики); Т — сидерический период обращения; Va — средняя линейная скорость движения по орбите; w — среднее угловое суточное движение планеты относительно Солнца (не путать со средним угловым суточным движением планеты относительно земного наблюдателя!); S — средний синодический период обращения (период повторения одноименной конфигурации планеты).
В табл. III.5 приведены физические характеристики планет. В этой таблице: М — масса в массах Земли (М0 = 5,98x1024кг); R — средний радиус планеты; р — средняя плотность; Е — сжатие; £ —-наклон оси вращения (наклонение экватора к орбите вращения); Р — период вращения (знак минус указывает на обратное вращение); Sut — продолжительность солнечных суток на планете; g — уско-
III.4. Параметры планетарных орбит
| Планета | а, астрономические единицы | е | i, градусы! минуты | т | w, градус за сутки | Va, км/с | S,сутки | |
| годы | годы и сутки | |||||||
| Меркурий | 0,387 | 0,206 | 7"00 | 0,241 | - 88 | 4,09 | 47,9 | (115,88) |
| Венера | 0,723 | 0,007 | Зв24' | 0,615 | - 225 | 1,60 | 35,0 | 584 (583,92) |
| Земля | 1,000 | 0,017 | - | 1,000 | 1 000 | 0,986 | 29,8 | - |
| Марс | 1,524 | 0,093 | Г51' | 1,881 | 1 322 | 0,524 | 24,1 | 780 (779,94) |
| Юпитер | 5,203 | 0,048 | 1"18> | 11,862 | 11 315 | 0,083 | 13,1 | 399 (398,88) |
| Сатурн | 9,539 | 0,055 | 2°29' | 29,458 | 29 167 | 0,034 | 9,6 | 378 (378,09) |
| Уран | 19,19 | 0,047 | 0°46' | 84,01 | 84 7 | 0,012 | 6,8 | (369,66) |
| Нептун | 30,07 | 0,008 | 1*47» | 164,79 | 164 280 | 0,006 | 5,4 | (367,48) |
| Плутон* | 39,52 | 0,253 | 174)8' | 247,70 | 248 150 | 0,004 | 4,7 | (366,74) |
* Элементы орбиты Плутона заметно меняются*
рение силы тяжести; Wn — критическая скорость на поверхности планеты (вторая космическая скорость). При этой скорости возмож-
 | |||
 |

|
но преодолеть притяжение планеты и покинуть ее, двигаясь по параболической орбите.
Ш.2. Спутники планет
Ш.2.1. Общий обзор
Все планеты Солнечной системы, кроме Меркурия и Венеры, обладают спутниками. Вокруг Земли обращается единственный ее спутник — Луна. У самой далекой планеты — Плутона в 1978 году обнаружили пока один спутник, названный Хароном.
Марс и Нептун имеют по два спутника. Первый спутник Нептуна — Тритон — был открыт еще в 1846 году. Это довольно большой спутник радиусом около 1850 км. Второй спутник Нептуна — Нереида — имеет значительно меньшие размеры (радиус около 150 км) и был обнаружен в 1949 году.
Спутники Марса Фобос и Деймос были открыты в 1877 году. Это глыбы неправильной округлой формы, имеющие соответственно 25 и 13,5 км в поперечнике.
До 1980 года считалось, что самым многочисленным семейством спутников обладает самая большая планета Солнечной системы — Юпитер. Первые четыре спутника Юпитера были открыты еще в 1610 году Галилеем, и их называют галилеевыми спутниками. Это Ио, Европа, Ганимед, Каллисто, — большие спутники. Радиус наименьшего из них — Европы — около 1450 км, а наибольшего —- Ганиме-да — около 2500 км. (Для сравнения радиус Луны 1738 км.) В 18^2 году был открыт самый близкий к Юпитеру и гораздо меньший спутник, названный впоследствии Амалътеей. Его оси 230 и 130 км.
С 1904 до 1974 года были открыты еще восемь значительно более далеких от Юпитера спутников. Семь из них имеют 20-30 км в поперечнике, один — около 100 км. Сейчас в семействе Юпитера известны 16 спутников.
Пять самых больших спутников Сатурна были открыты в XVII веке. Это Тефия, Диона, Титан, Япет и Рея. Наибольший из них

 Титан, имеющий радиус около 2800 км. Радиусы остальных четырех от 410 до 800 км. В XVIII-XIX веках были открыты еще четыре спутника меньших размеров. Это Мимас, Энцелад, Гиперион и Феба (самый далекий от планеты). В 1966 году был открыт десятый спутник Сатурна — Янус, — самый небольшой и самый близкий к Сатурну. В 1974 году, пролетая мимо Сатурна, американский "Пионер-11" обнаружил еще два небольших спутника, а "Вояджер-1" и "Вояджер-2" сфотографировали еще пять небольших спутников. Сейчас в семействе Сатурна известны 17 спутников, и пока оно самое многочисленное.
Титан, имеющий радиус около 2800 км. Радиусы остальных четырех от 410 до 800 км. В XVIII-XIX веках были открыты еще четыре спутника меньших размеров. Это Мимас, Энцелад, Гиперион и Феба (самый далекий от планеты). В 1966 году был открыт десятый спутник Сатурна — Янус, — самый небольшой и самый близкий к Сатурну. В 1974 году, пролетая мимо Сатурна, американский "Пионер-11" обнаружил еще два небольших спутника, а "Вояджер-1" и "Вояджер-2" сфотографировали еще пять небольших спутников. Сейчас в семействе Сатурна известны 17 спутников, и пока оно самое многочисленное.

|
Четыре самых больших спутника Урана были открыты в XVIII-XIX веках: Ариэль, Умбриэль, Титания, Оберон. Радиусы их от 300 до 600 км. В 1948 году был открыт пятый спутник — Миранда (радиус около 250 км). В январе 1986 года "Вояджер-2", пролетая вблизи Урана, сфотографировал еще 10 спутников, близких к планете. Девять из них имеют от 15 до 100 км в поперечнике, а один — около 160 км. Семейство Урана насчитывает 15 спутников.
Планеты-гиганты Юпитер, Сатурн и Уран окружены не только спутниками, но также удивительными образованиями — кольцами вокруг планеты. У Сатурна кольцо было обнаружено еще в XVII веке голландским механиком и астрономом Христианом Гюйгенсом (рис. III.7).
Считалось, что Сатурн окружен по крайней мере тремя кольцами, но недавно обнаружены новые кольца, вложенные одно в другое и разделенные сравнительно узкими "щелями". Одно из них состоит из крупных тел, имеющих 20-30 км в поперечнике, расположенных не особенно близко друг к другу. Другие кольца состоят из множества мелких частиц и более крупных тел размерами от нескольких сантиметров до 1 км в поперечнике.
Date: 2015-11-13; view: 1486; Нарушение авторских прав