Косозубые и шевронные цилиндрические передачи

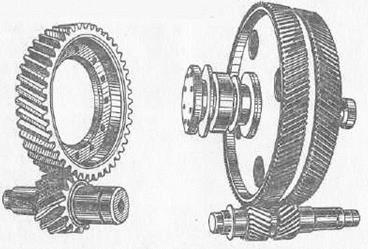
У косозубых колес зубья располагаются не по образующей делительного цилиндра, а составляют с ней некоторый угол b= 8...40°. (рис. 5.35,а; 5.36,а). Такая конструкция приводит к осевым силам. В шевронных зубьях компенсируются осевые нагрузки и зубья расположены V- образно (рис.5.35,б; 5.36,б). Оси колес параллельны. Для нарезания косых зубьев используют инструмент такого же исходного контура, как и для нарезания прямых зубьев. Поэтому профиль косого зуба в нормальном сечении n-n совпадает с профилем прямого зуба. Модуль в этом сечении должен быть также стандартным.

а) б)

Рис. 5.35 Пары с косозубыми (а) и шевронными (б) колесами.

а) б)

Рис. 5.36 Геометрические особенности косозубой (а) и шевронной (б)

зубчатых пар

В торцовом сечении t-t параметры косого зуба изменяются в зависимости от угла b:

окружной шаг P_t= P_n/ cos b;

окружной модуль m_t= m_n/ cosb;

делительный диаметр d= m_t z= m_nz/ cosb. (5-42)

Индексы n и t приписывают параметрам в нормальном и торцовом сечениях соответственно.

Рис. 5.37

К вопросу об эквивалентном прямозубом колесе.

Прочность зуба определяют его размеры и форма в нормальном сечении. Форму косого зуба в нормальном сечении принято определять через параметры эквивалентного прямозубого колеса (рис.5.37).

Нормальное к зубу сечение образует эллипс с полуосями c= r и e= r/cosb, где r= d/2. В зацеплении участвуют зубья, расположенные на малой оси эллипса, т.к. второе колесо находится на расстоянии c= d/2. Радиус кривизны эллипса на малой оси

r_u= e²/c= r/cos²b.

В соответствии с этим форма косого зуба в нормальном сечении определяется эквиваленитным прямозубым колесом, диаметр которого

d_u= d/ cos²b

и числом зубьев

z_u= d_u / m_n= d/(m_ncos²b)= m_t z /(m_t cos³b)

или z_u= z/cos³b.

Так, при b= 20°, d_u= 1,13d; z_u= 1,2 z.

Увеличение эквивалентных параметров (d_u и z_u) с увеличением угла b является одной из причин повышения прочности косозубых передач. Вследствие наклона зубьев получается колесо как бы больших размеров или при той же нагрузке уменьшаются габариты передачи. Кроме того, здесь имеет место многопарность зацепления, уменьшение шума и др. Поэтому в современных передачах косозубые колеса получили преимущественное распространение.

В отличие от прямых косые зубья входят в зацепление постепенно. Оно здесь распространяется от точек 1 к точкам 2 (рис.5.36).

Косозубое зацепление не имеет зоны однопарного зацепления. В прямозубом зацеплении нагрузка с одного зуба на другой передается мгновенно, что сопровождается шумом, колебаниями.

В косозубых передачах зубья нагружаются постепенно. Плавность косозубого зацепления значительно снижает шум и динамические нагрузки. Последнее особенно ощутимо в быстроходных передачах.

Косозубые колеса могут работать без нарушения зацепления, если обеспечено осевое перекрытие, определяемое из соотношения

e_b= b_wtgb/P_bt» b_wsinb/ (pm_n),(рекомендуют e_b³ 1,1). (5-43)

даже при коэффициенте торцевого перекрытия e_a< 1, которое определяется с помощью формулы

e_a= 1,88- 3,2(z^-1₁± z^-1₂)cos b. (5-44)

Здесь знак «+»- для внешнего, а «-» -для внутреннего зацепления.

Рекомендуют принимать для косозубых передач e_b³ 1.

В косозубом зацеплении нагрузка распределяется на всю длину контактных линий, равную

l_å= b_w e_a/cosb.

Т.е. чем больше угол b, тем больше l_å, но во избежание больших осевых сил рекомендуют принимать b= 8°....20°. В шевронных колесах может быть b= 40°.

Через крутящий момент, передаваемый зубчатой парой, определяется окружная сила

F_t= 2M_кр/d. (5-45)

которая является одной из составляющих нормальной силы

F_n= F’_t/ cos a_w, (5-46)

где F’_t= F_t/cosb.

Другими составляющими являются

радиальная сила

F_r= F’_ttga_w, (5-47)

осевая сила

F_а= F_ttgb. (5-48)

Нормальные напряжения в контактирующих поверхностях можно рассчитать по выражению

s_Н= 1,18Z_Hb {E_npM_кр1К_Н (u± 1)u^-1[d²_w1b_wsin(2a_w)]}^1/2£ [s_Н], (5-49)

где Z_Hb= (K_Hacos²b/e_a)^1/2- коэффициент повышения прочности косозубых передач по контактным напряжениям (K_Ha - берется из таблиц); b_w - ширина зуба; [s_Н] - допускаемое контактное напряжение (определение его будет рассмотрено ниже). Знак “-” берется для внутреннего зацепления.

В начале расчета можно коэффициент ширины колеса отноcительно межосевого расстояния принять равным y_ba= 0,4, а коэффициент K_Hb = 1.

Тогда при известных u, [s_H], Е_пр можно рассчитать межосевое расстояние

A» 0,75(u+1){E_npМ_кр2K_Hb/([s_H]²u²y_ba)}^1/3. (5-50)

Полученное значение округляется до значений ряда, а затем определяется ширина колеса

b’_w= y_baA.

Затем по таблице принимается значение коэффициента y_m= b_w/m. Для обычных редукторов принимают y_m=30. Тогда нормальный модуль зацепления будет

m_n = b’_w/y_m. (5-51)

Полученное значение округляется по ряду.

После этого находится число зубьев

суммарное z_å= 2A/m_n;

шестерни z₁= z_å/(u+1);

колеса z₂= z_å- z₁.

Полученные значения затем округляются до целого.

Далее определяются делительные диаметры

шестерни d₁= z₁m_n; колеса - d₂= z₂m_n.

Следуя практическим рекомендациям, выбираем коэффициент торцевого перекрытия e_b = 1,2 и определяем угол

b= arcsin(pe_bm_n/b_w). (5-52)

Далее с учетом наклона зубьев вычисляем

z’₁= d₁cosb/m_n; z’₂= d₂cosb/m_n. (5-53)

При этом целесообразно выполнять неравенство z’₁>16, а число зубьев должно быть целым.

Уточняем значение b, который не должен быть меньше 8°

b= arccos [0,5(z₁+ z₂)m_n/A]. (5-54)

Если этот угол меньше 8°, то следует варьированием числом зубьев колес получить величину b³ 8° и при этом отклонения значения фактического передаточного числа от заданного не должно превышать 4%.

Делительные диаметры колес будут d₁= mz₁/cos b; d₂= mz₂/ cos b.

После этого производится проверочный расчет на прочность.

Определяется окружная скорость u= pd₁n₁/60 [м/с].

Назначается степень точности, часто 9-я.

Вычисляется коэффициент y_bd= 0,5y_ba(u+1).

На основании этих данных определяется коэффициент K_Нu; c учетом расположения колес и величины коэффициента y_bd определяется коэффициент K_Hb, а затем и коэффициент K_H= K _Нu K_Hb.

После этого в зависимости от окружной скорости и выбранной степени точности определяется коэффициент неравномерности нагрузки одновременно зацепляющихся пар зубьев K_Ha.

После вычисления коэффициентов e_a, Z_Hb по формулам, соответственно, (5-44), (5-49) при a = 20° по формуле (5-49) определяется контактное напряжение s_H. Разница между этим значением и допускаемым напряжением не должна превышать 4%.

Далее вычисляются эквивалентные числа зубьев шестерни и колеса

z_u1= z₁/cos³b; z_u2= z₂/cos³b.

По графику определяются коэффициенты формы зуба Y_F1, Y_F2, а затем отношения [s_F1]/ Y_F1, [s_F2]/ Y_F2 и для колеса с меньшим значением этого отношения проверяется прочность зуба на изгиб.

Перед этим в зависимости от окружной скорости и принятой степени точности по таблицам выбираются коэффициенты K_Fa, K_Fb, а также в зависимости от конструкции передачи и коэффициента y_bd - коэффициент K_Fu. Откуда K_F= K_FuK_Fb, Определяется коэффициент повышения прочности косозубых передач по напряжениям изгиба Z_Fb= =K_Fa(1- b°/140)/e_a.

s_F2= Y_F2Z_FbF_tK_F/(b_wm_n). (5-55)

Date: 2015-11-13; view: 658; Нарушение авторских прав