Основное уравнение динамики вращательного движения твердого тела

(5.10)

Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела , равно импульсу момента всех внешних сил, действующих на это тело.

10. Работа постоянной и переменной силы.

1.Если на тело действует постоянная сила F (Рисунок 13), и это приводит к перемещению ∆ r тела, то элементарной работой ∆А постоянной силы называется скалярное произведение вектора силы F и вектора перемещения ∆ r:

∆А = (F ∙∆ r) = ½ F ½½∆ r ½ cos a,

где a - угол между направлениями векторов силы F и перемещения ∆ r, (F ∙ ∆ r) – скалярное произведение двух векторов (см.[8]).

Рисунок 13 - Перемещение тела под действием постоянной силы.

Работа ∆А - скаляр. Если угол a - острый, то ∆А положительная величина, и говорят, что сила совершает работу. Если угол a - тупой, то ∆А - отрицательная величина, и говорят, что работа совершается против действия силы. Если a = 90⁰, т.е. направления силы и перемещения взаимно перпендикулярны, то такая сила работы не совершает ∆А = 0. Такая сила не может изменить величину скорости тела, но она меняет направление скорости.

2. Работа переменной силы. Если сила или равнодействующая сил изменяет свою величину или направление (движение по криволинейной траектории, причем угол α ≠ 90⁰), то работа ∆А, совершаемая переменной силой F (или F рез) на конечном участке траектории вычисляется следующим образом.

На рисунке 14 представлен график зависимости силы F от пути S. Разобьем весь путь на N участков. Перемещение и действующая сила на каждом участке соответственно равны F _i и ∆ r _i. Тогда работа А, совершаемая силой F, равна алгебраической сумме работ, совершаемых каждой из сил F _i на своем малом участке (Рисунок 14):

А = ∆А₁ + ∆А₂ +....+ ∆А _N = (F ₁∙∆ r ₁) + (F ₂∙∆ r ₂) +...+(F _N∙∆ r _N) = (F _i∙∆ r _i),

где i = 1,2...... N - номер элементарного участка траектории.

Рисунок 14 - График зависимости силы от пути.

На участке ∆ r _i силу F _i можно считать постоянной, тогда элементарная работа ∆А_i на участке ∆ r _iравна ∆А_i = F _i∙∆ r _i и равна площади заштрихованной фигуры на рисунке 14.

А= ∆А_i - это работа силы F на участке r, равна она численно площади S фигуры, ограниченной кривой зависимости F(х) и осью Х.

11. Кинетическая энергия. Теорема о кинетической энергии.

*величины - половины произведения массы тела на квадрат его скорости. Эта величина имеет особое название - кинетическая энергия.

кинетическая энергия - это физическая величина, характеризующая движущееся тело; изменение этой величины равно работе силы, приложенной к телу.

*A = E_k2 - E_k1 Работа силы равна изменению кинетической энергии тела. Это утверждение называется теоремой о кинетической энергии.

12. Работа при вращательном движении твердого тела.

За время dt вращающееся тело совершит работу dA, равную произведению момента силы M на угол поворота , сделанный радиусом этого тела, то есть

.

13. Кинетическая энергия вращательного движения.

Кинетическая энергия материальной точки W_k = mv² / 2.

Тогда для системы материальных точек или тела .

Используя связь линейной скорости с угловой в виде v_i = wr_i, получим выражение для энергии вращательного движения:

(5.20)

Замечание: При плоском движении тел (например, цилиндр скатывается по наклонной плоскости, рис. 5.12) полная скорость

,

(5.21)

где с - центр масс (инерции).

Полная кинетическая энергия тела равна сумме кинетической энергии поступательного движения его центра масс (центра инерции) и кинетической энергии вращательного движения тела относительно мгновенной оси)*, т.е.

.

(5.22)

14. Потенциальная энергия. Свойства потенциальных сил. Связь между силами поля и потенциальной энергией. Потенциальная энергия гравитационной и упругой сил.

Потенциальная энергия - энергия взаимодействия тел или частей тела. Потенциальная энергия (от латинского potentia - возможность) определяется взаимным расположением тел или частей тела, т.е. расстояниями между ними.
Потенциальная энергия тела, поднятого над Землей. Работа силы тяжести.
Пусть тело свободно падает с высоты h1 над уровнем Земли на уровень h2. Тогда: 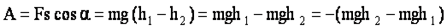  При падении сила тяжести совершает положительную работу, при движении тела вверх - отрицательную. Величину Eз = mghназывают потенциальной энергией взаимодействия тела и Земли.
Т.о. A = - (Ep2 - Ep1) = -DEp Работа сила тяжести равна изменению потенциальной энергии, взятому с противоположным знаком. Т.е., если потенциальная энергия увеличивается (тело поднимается), то сила тяжести совершает отрицательную работу и наоборот.	Eз = mgh A = - (Ep2 - Ep1) = -DEp
Т.к. потенциальная энергия определяется координатой, то величина потенциальной энергии определяется выбором системы координат (выбором нулевого уровня). Т.е. она определяется с точностью до постоянной величины. В данной задаче удобно за точку отсчета выбирать уровень Земли.
Если тело движется под углом к направлению вектора силы тяжести, то, как видно из рисунка, работа силы тяжести независимо от траектории определяется изменением положения тела (на рис. - высотой наклонной плоскости h). Если тело движется по произвольной траектории, то ее можно представить в виде суммы горизонтальных участков, на которых работа силы тяжести равна нулю, и вертикальных, на которых суммарная работа будет равна А=mgh. Работа силы тяжести не зависит от формы траектории и определяется только начальным и конечным положением тела. На замкнутой траектории работа силы тяжести равна нулю, т.к. потенциальная энергия не меняется.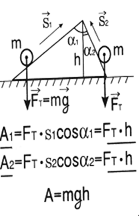
Потенциальная энергия тел, взаимодействующих посредством гравитационных сил.
,   где r- расстояние между взаимодействующими телами. Знак "-" говорит о том, что это энергия притягивающихся тел. При сближении тел потенциальная энергия увеличивается по модулю. Работа по сближению двух астрономических объектов: .
Потенциальная энергия упруго деформированного тела. Работа силы упругости.
Для вывода формулы используем, что работа численной равна площади под графиком зависимости силы от координаты. При малых упругих деформациях сила упругости прямо пропорциональна абсолютной деформации (з-н Гука) - см. рис. Тогда работа при изменении деформации от х1 до х2 равна: .
Учитывая з-н Гука, получим: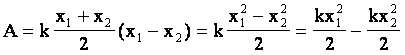
Т.о., если принять за потенциальную энергию упруго деформированного тела величину ,   где k - коэффициент жесткости, а х - абсолютная деформация тела, то можно сделать вывод, что ,   т.е. работа силы при деформации тела равна изменению потенциальной энергии этого тела, взятой с обратным знаком.
Работа силы упругости зависит только от координат (начальной и конечной деформаций) тела и, следовательно, не зависит от траектории. Работа по замкнутой траектории равна нулю.
Консервативные силы. Консервативными (сохраняющими) наз. силы, работа которых не зависит от траектории и по замкнутой траектории равна нулю (эти силы не зависят от скоростей). Примеры: гравитационные, упругие.
Диссипативные силы Диссипативными (рассеивающими) наз. силы, работа которых зависит от траектории и по замкнутой траектории не равна нулю (такие силы зависят от скорости). Пример: сила трения.

15. Законы изменения и сохранения энергии в механике, границы их применимости.

Полная энергия системы неизменна. Существуют три вида энергии-потенциальная E(формула: Eр=mgh в механике или W=qEd в электродинамике), кинетическая (формула E=m v v/2) и внутренняя. Эти энергии могут переходить друг в друга. Например с некоторой высоты к земле летит камень.. Потенциальная энергия его при этом уменьшается, а кинетическая увеличевается. Изменение кинетической энергии равно отрицательному изменению потенциальной энергии, поэтому полная энергия системы неизменна.
Но энергия никуда не исчезает-поэтому, когда камень упадёт на землю, его кинетическая энергия переходит во внутреннюю.

Молекулярная физика

1. Молекулярно-кинетическая теория идеальных газов-основные положения и управления состояния. Равновесные состояния и процессы. Абсолютный иоль.

*Основные положения молекулярно-кинетической теории:
1)Все вещества состоят из мельчайших частиц - атомов и молекул.
2)Молекулы и атомы любого вещества находятся в непрерывном хаотическом движении, которое называется тепловым движением. При нагревании вещества интенсивность движения частиц увеличивается.
3)Молекулы вещества взаимодействуют между собой с силами притяжения Fпр и отталкивания Fот.
r = r0, Fот = Fпр,

r < r0, Fот > Fпр,

r > r0, Fот < Fпр,

r, F 0.

Характер движения молекул зависит от агрегатного состояния вещества.

Движение молекул газов сводится к хаотическому поступательному движению.

Скорость молекул газов зависит от температуры.
Масса молекулы:
Молекулярная масса вещества – масса молекулы вещества, выраженная в а.е.м.
Атомная единица массы (а.е.м.) – единица массы, равная 1/12 массы атома С12.
Моль – количество вещества, в котором содержится число молекул, равное числу атомов в 0,012 кг изотопа углерода С12.
Число частиц, содержащихся в моле вещества, называется числом Авогадро:
N_A = 6,023 1023 моль-1
Молярная масса М – масса моля вещества.
Зная число Авогадро, можно найти значение а.е.м.
0,012 = N_A 12 1 а.е.м.,

Размеры молекулы:
Линейные размеры молекул воды приблизительно равны 3 10^-10 м.

* Для описания состояния термодинамической системы вводятся физические величины, которые называются термодинамическими параметрами или параметрами состояния системы. Обычно в качестве термодинамических параметров выбирают давление P, объем V и температуру T.

Температура – это макроскопический параметр, характеризующий различную степень нагретости тел. Это одна из макроскопических характеристик внутреннего состояния тел. Понятие температуры имеет смысл для равновесных состояний термодинамической системы. Равновесным состоянием (состоянием термодинамического равновесия) называется состояние системы, не изменяющееся с течением времени (стационарное состояние), причем стационарность состояния не связана с процессами, происходящими во внешней среде. Равновесное состояние устанавливается в системе при постоянных внешних условиях и сохраняется в системе произвольно долгое время. Во всех частях термодинамической системы, находящейся в состоянии термодинамического равновесия, температура одинакова.
В термодинамической шкале температур температура измеряется в кельвинах (К) и обозначается Т.

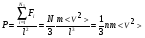
Соотношение, устанавливающее связь между параметрами состояния системы называется уравнением состояния термодинамической системы. Если какой либо из термодинамических параметров системы изменяется, то происходит изменение состояния системы, называемое термодинамическим процессом. Термодинамический процесс называется равновесным, если система бесконечно медленно проходит непрерывный ряд бесконечно близких термодинамических равновесных состояний. Изопроцессами называются термодинамические процессы, происходящие в системе с постоянной массой при каком либо одном постоянном параметре состояния.

Идеальным газом называется газ, молекулы которого не взаимодействуют друг с другом на расстоянии и имеют исчезающе малые собственные размеры. Состояние заданной массы m идеального газа определяется значениями трёх параметров: давления P, объёма V, и температуры Т. Соотношение, устанавливающее связь между этими параметрами, имеет вид:
PV=(m/M)RT - уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)
где М - масса 1 моля газа, R = 8,31 Дж/мольК универсальная газовая постоянная.
Для одного моля газа уравнение состояния идеального газа примет вид:
PV/T=R=const - уравнение Клапейрона.

Рассмотрим теперь изопроцессы для идеального газа:

1)T = const – изотермический процесс.

PV = const – закон Бойля-Мариотта

2)P = const - изобарический процесс.

V/T=const закон Гей-Люссака.

3)V = const – изохорический процесс

P /T= const - закон Шарля.

Запишем уравнение состояния идеального газа в другой форме.

Введем новую постоянную величину:

- постоянная Больцмана
и перепишем уравнение Менделеева-Клапейрона в виде: PV=(m/M)N_AkT
Учитывая, что (m/M)NA=N - число молекул в газе массы m, получим PV= nkT => P=(N/V)kT
Так как N/V=n - число молекул в единице объема или концентрация молекул, то P=nkT - другая форма записи уравнения состояния идеального газа.
3. Основное уравнение молекулярно – кинетической
теории газов.
Возьмем сосуд в форме куба с ребром L с газом и определим давление P газа на стенки сосуда.

1)Вдоль оси х движется одна треть всех молекул, т.е.;
2)Удар молекул о стенку Q идеально упругий и молекулы проходят расстояние, равное размеру куба, не испытывая соударений.

Импульс силы, полученный стенкой при ударе молекулы, определим из второго закона Ньютона:

где - изменение импульса молекулы, m – масса молекулы.

Одна молекула одна молекула за время t передает стенке импульс силы
,а за время t=1сек передаёт стенке импульс силы равный F*1=2mVk,
где k – число ударов молекул за 1 сек.
Так как - промежуток времени между двумя последовательными ударами,. то K=1/t=V/2L, тогда F*1=m V²/L
Теперь подсчитаем суммарный импульс силы, который передают стенке N1 молекул, движущихся вдоль оси x, за 1 сек
средняя квадратичная скорость молекул газа

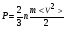
Давление, оказываемое газом на грань куба, где n – концентрация молекул. Запишем это выражение в виде:
средняя кинетическая энергия поступательного движения молекулы.

основное уравнение молекулярно-кинетической теории (уравнение Клаузиуса)
С учетом уравнения состояния идеального газа: P=nkT

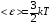
получаем выражение для средней кинетической энергии поступательного движения молекул:
kT есть мера энергии теплового движения молекул.
Молекулярно- кинетическое толкование абсолютной температуры:
А. т. – есть величина, пропорциональная средней энергии поступательного движения молекул.

* Абсолю́тный нуль температу́ры (реже — абсолютный ноль температуры) — минимальный предел температуры, которую может иметь физическое тело во Вселенной. Абсолютный нуль служит началом отсчёта абсолютной температурной шкалы, например, шкалы Кельвина. В 1954 X Генеральная конференция по мерам и весам установила термодинамическую температурную шкалу с одной реперной точкой — тройной точкой воды, температура которой принята 273,16 К (точно), что соответствует 0,01 °C, так что по шкале Цельсия абсолютному нулю соответствует температура −273,15 °C.

* Термодинамическое равновесие — состояние системы, при котором остаются неизменными по времени макроскопические величины этой системы (температура, давление, объём,энтропия) в условиях изолированности от окружающей среды. В общем, эти величины не являются постоянными, они лишь флуктуируют (колеблются) возле своих средних значений. Если равновесной системе соответствует несколько состояний, в каждом из которых система может находиться неопределенно долго, то о системе говорят, что она находится в метастабильном равновесии. В состоянии равновесия в системе отсутствуют потоки материи или энергии, неравновесные потенциалы (или движущие силы), изменения количества присутствующих фаз. Отличают тепловое, механическое, радиационное (лучистое) и химическое равновесия. На практике условие изолированности означает, что процессы установления равновесия протекают гораздо быстрее, чем происходят изменения на границах системы (то есть изменения внешних по отношению к системе условий), и осуществляется обмен системы с окружением веществом и энергией. Иными словами, термодинамическое равновесие достигается, если скорость релаксационных процессов достаточно велика (как правило, это характерно для высокотемпературных процессов) либо велико время для достижения равновесия (этот случай имеет место в геологических процессах).

2. Максвелловское распределение молекул по скоростям. Больцмановское распределение молекул в потенциальном поле. Барометрическая формула.

3. Явление переноса: диффузии, теплопроводности и внутреннего трения.

4. Первое начало термодинамики. Применение первого начала термодинамики к различным изопроцессам. Адиабатный и политропный процессы.

5. Обратимые и необратимые процессы. Круговые процессы. Цикл карно. Энтропия как фулкция состояния. Второе третье начала термодинамики.

6. Силы и потенциальная энергия межмолекулярного взаимодействия. Реальные газы. Уравнение Ван-дер-Ваальса. Изотермы реального газа. Критическое состояние вещества. Внутренняя энергия реального газа.

7. Теплоемкость многоатомных газов. Зависимость теплоемкости от вида процесса. Недостаточность классической теплоемкости.

8. Характеристика жидкого состояния. Поверхностное натяжение. Явление смачивания и несмачивания. Формула Лапласа. Капиллярные явления. Понятие о перхностно-активных веществах.

9. Фазовые равновесия и фазовые превращения. Фазовая диаграмма. Тройная точка. Уравнение Клапейрона-Клаузиса.

10. Фазовые переходы.

Date: 2015-11-13; view: 984; Нарушение авторских прав