Естественный» способ описания движения

Этот способ описания движения применяют в том случае, когда траектория движения точки заранее известна. Положение точки на траектории задают дуговой координатой 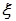(кси)[1]. На траектории стрелкой указывают положительное направление дуговой координаты.

Уравнением движения является зависимость координаты 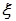от времени, т.е.:

(1.17)

Скорость точки. Введем единичный вектор , связанный с движущейся точкой 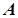и направленный по касательной к траектории в сторону возрастания дуговой координаты 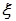(см. рис. 1.3). Вектор при движении точки изменяет свое направление, и, следовательно, не является постоянным вектором. Вектор мгновенной скорости связан с ортом соотношением:

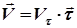, (1.18)

где 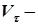проекция вектора скорости на направление вектора и равна производной от дуговой координаты по времени, т.е.:

. (1.19)

Ускорение точки. Вектор полного ускорения точки находят дифференцированием равенства (1.17) по времени, в результате чего получают равенство:

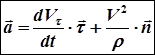, (1.20)

где 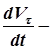производная от проекции вектора скорости на направление вектора по времени, единичный вектор нормали, а 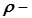радиус кривизны траектории в точке 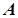. Первое слагаемое в правой части (1.20) это составляющая вектора полного ускорения на направление вектора , называемая тангенциальным ускорением, т.е.:

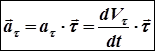, (1.21)

где 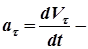проекция тангенциального ускорения на направление вектора . Тангенциальное ускорение показывает, как быстро меняется величина вектора скорости со временем.

Второе слагаемое в правой части равенства (1.20) представляет собой составляющую вектора полного ускорения, направленную на направление вектора нормали , и называется нормальным ускорением. Нормальное ускорение характеризует быстроту изменения направления вектора скорости. Величина нормального ускорения находится по формуле:

. (1.22)

Модуль вектора полного ускорения находится по формуле:

. (1.23)

Движение с постоянным по величине тангенциальным ускорением описывается уравнением:

, (1.24)

Зависимость проекции скорости от времени:

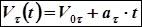(1.25)

где величина дуговой координаты в начальный момент времени, 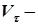проекция вектора скорости на направление вектора , тангенциальное ускорение.

Правило знаков. Величина 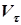положительная, если точка движется в направлении вектора (или в направлении возрастания дуговой координаты 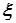), в противном случае, величина 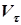отрицательная. Знак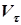и и совпадают при ускоренном движении, при замедленном движении – знаки противоположны.

2. Кинематика вращательного движения. Угловые скорости и ускорения (средние и мгновенные), связь между линейными и угловыми величинами.

Date: 2015-11-13; view: 530; Нарушение авторских прав