Дано Решение

x = At, y = At (1 + Bt)	Исключим время из уравнения для и подставим полученное выражение в уравнение для : ; .
y(x) –? (t) –? a (t) –? r (t) –?

Запишем выражение для радиуса–вектора :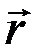

.

Скорость – это первая производная от радиуса–вектора по времени:

.

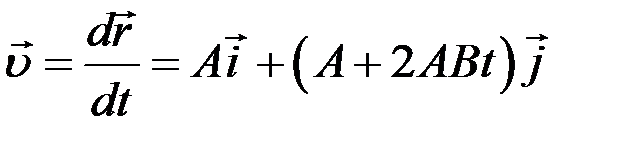Так как вектор можно представить как сумму векторов:

,

тогда , , а величина скорости:

.

Ускорение есть первая производная по времени от скорости:

.

В то же время .

Таким образом, . Модуль вектора равен:

.

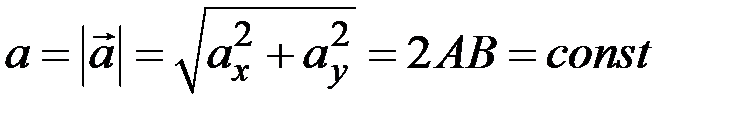Ответ: 1) 2)

3) 4)

Задачи

1. Зависимость пройденного телом пути S от времени дается уравнением S = A+Bt+Ct+Dt³, где С = 0,14 м/с² и D = 0,01 м/с³. Через какое время после начала движения тело будет иметь ускорение а = 1 м/с²? Найти среднее ускорение < а > тела за этот промежуток времени.

2. Зависимость пройденного телом пути s от времени t дается уравнением , где м, м/с и м/с². Найти ускорение и среднюю скорость < > тела за первую, вторую и третью секунды его движений.

3. Тело падает высоты км с нулевой начальной скоростью. Пренебрегая сопротивлением воздуха, определите, какое время понадобится телу для прохождения: 1)первых 10 м пути; 2) последних 10 м пути.

4. Зависимость пройденного телом пути от времени задается уравнением ( м/с² , м/с³). Определите:

1)через сколько времени после начала движения ускорение тела будет равно 2 м/с² ; 2) среднее ускорение < > тела за этот промежуток времени.

5. Уравнения движения двух материальных точек имеют вид и , где , м/с², м/с². Определите: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорения и для этого момента.

6. За пятую секунду равнозамедленного движения точка проходит

5 см и останавливается. Какой путь проходит точка за третью секунду этого движения.

7. Уравнения скорости имеют вид: (величины измерены в единицах СИ). Запишите уравнения движения и постройте графики скорости и пути от времени.

8. В последнюю секунду свободного падения тело прошло путь в двое больший, чем в предыдущую секунду. С какой высоты падало тело.

9. Камень, брошенный вертикально вверх, упал на землю через 2 с. Определите путь и перемещение камня за 1, 1,5 и 2 с. Какую скорость приобретёт камень за эти промежутки времени? Чему равна средняя скорость перемещения камня за всё время движения.

10. Мячик брошен вертикально вверх из точки, находящийся на высоте . Определите начальную скорость мячика, время движения и скорость падения, если известно, что за время движения он пролетел путь 3 .

11. В течении времени скорость тела задаётся уравнением вида . Определить среднюю скорость за промежуток времени .

12. При падении камня в колодец его удар о поверхность воды доносится через . Принимая скорость звука , определите глубину колодца.

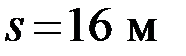13. Тело движется равноускоренно с начальной скоростью . Определите ускорение тела, если за время оно прошло путь и его скорость .

14. Материальная точка движется вдоль прямой так, что её ускорение линейно растёт и за первые 10 с достигает значения 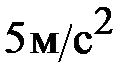. Определите в конце десятой секунды: 1) скорость точки; 2) пройденный точкой путь.

15. Зависимость пройденного телом пути от времени выражается уравнением . Запишите выражения для скорости и ускорения. Определите для момента времени после начала движения: 1) пройденный путь; 2) скорость; 3) ускорение.

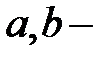16. Точка движется в плоскости из положения с координатами со скоростью ( постоянные, орты осей и ). Определите: 1) уравнение траектории точки ; 2) форму траектории.

17. Радиус – вектор материальной точки изменяется со временем по закону , где орты осей и . Определите для момента времени : 1) модуль скорости; 2) модуль ускорения.

18. Материальная точка движется по прямой. Уравнение её движения . Определить мгновенную скорость и ускорение точки в конце второй секунды от начала движения, среднюю скорость и путь, пройденный за это время.

19. Движение двух тел описывается уравнениями

, . Определите величину скоростей этих тел и момент времени, когда ускорения их будут одинаковы, а также значение ускорения в этот момент времени.

20. Материальная точка, двигаясь прямолинейно с постоянным ускорением, за пятую секунду движения прошла путь . Начальная скорость . Найти ускорение точки.

Date: 2015-11-13; view: 1386; Нарушение авторских прав