
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Topic: Propositional logic
|
|
Originally the 2-value Boolean logic was developed by John Boole (England, 1823-1864) to explore which Natural language statements are logically sound and which are not. For some decades this mathematical tool had no practical application. Later it was found that the 2-value Boolean logic is very convenient for performance description of electrical circuits with switches, compute electronic circuits and other systems.
Definitions:
 A statement is any sentence that can be true of false(has a truth value).
A statement is any sentence that can be true of false(has a truth value).
"Kharkov is a city."(true)
"Now it is summer."(false) statements
"Some birds can fly."(true)
 |
"Go home!"(order) not statements
"What is your name?"(question)
 |
"What I am saying is not true"
" A barber shaves everybody who do not shave themselves"
These are paradoxical statements: they have hidden contradiction. It is impossible to say if they are true of false.
Statements can be simple or compound.
|
 Examples of simple statements:
Examples of simple statements:
"Today is Friday."
"It is sunny now."
"2+3=5"
"2+2=6"
Compound statements are made up of one or more simple (or compound) statements that are linked together by connectives. Five basic connectives:
- not
- and
- or
- if...then...
-if and only if...
Examples of compound statements:
- It is not Monday.
- It is raining and the sky is cloudy.
- If today is Saturday then I must not go to work.
- 5* x=5 if and only if x=1.
- if x=2 and y=3 then x+y=100.
- The sun is not shining if and only if tomorrow is Saturday and there are no clouds in the sky.
Note: A compound statement does not have to make much sense.
An inductive (formal) definition of a compound statement:
1) All simple statements are compound statements.
2) If S and T are compound statements then
a) (not S) is a compound statement
b)(S and T) is a compound statement
c) (S or T) is a compound statement
d) (if S then T) is a compound statement
e) (S if and only if T) is a compound statement
3) Nothing is a compound statement unless it can be obtained by a finite number of applications of steps 1 and 2.
Note: Mathematical logic cannot tell if a simple statement is true or false. This we must decide by other means. The goal of the mathematical logic is to tell us whether a compound statement is true or false, depending on the truth values of its simple statements.
Example:

 " Today it is Wednesday and it is raining."
" Today it is Wednesday and it is raining."
statement p statement q
|
The structure of the above compound statement in a symbolic form:.
Here p, q are simple statements.
Note: In mathematical logic it is the logical structure of a compound statement that is important, not its individual simple statements.
" I am a teacher and 2+2=5"
|
All have the same logical structure and may be viewed as the same statement from logical point of view.
The precise meaning of each of the five basic connectives is defined by such truth tables:
conjunction (p  q) disjunction (p
q) disjunction (p  q) negation ~p
q) negation ~p
| p | q | p and q | p | q | P or q | p | not p | ||||
| T | T | T | T | T | T | T | F | ||||
| T | F | F | T | F | T | F | T | ||||
| F | T | F | F | T | T | ||||||
| F | F | F | F | F | F |
p ® q (conditional) p «q (biconditional)
| p | q | If p then q |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
| p | q | p if only if q |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
Note: Sentences: " if p then q", " p only if q", " p implies q" - all have the same logical meaning.
 Note: Lines 3 and 4 in the table for p q represent such a common sense concept:" If an assumption is wrong then any conclusion is acceptable because nobody bothers to consider it."
Note: Lines 3 and 4 in the table for p q represent such a common sense concept:" If an assumption is wrong then any conclusion is acceptable because nobody bothers to consider it."
Ex: If 2*2=5 then I am the mother of Napoleon. (true)
If 2*2=5 then 3*2=6. (true)
In such cases we should not consider what is after "then".
Examples of transforming compound statements into symbolic forms:
"John is in the library or he is not at the book store."(1)
p=" John is in the library." q= " John is in the book store."
The symbolic form of statement (1): p  ~q.
~q.
" If today is Monday or it is not raining then we can go to the store". (2)
p="Today is Monday." q= "it is raining". z = " we can go to the store"
 The symbolic form for statement (2): p
The symbolic form for statement (2): p  ~q r.
~q r.
Ex: Let p="I study", q=" I will pass the course."

 The formula (p q)
The formula (p q)  (~p ~q) is the symbolic form of the statement:
(~p ~q) is the symbolic form of the statement:
" If I study, then I will pass this course and if I do not study, then I will not pass this course."
Note: Letters p, q, etc, in symbolic forms are called statement variables of the compound statement.
Self test questions:
1.) Which of the following are statements?
a)All men are created equal.
b)John.
c) No smoking
d) Are you ready?
2.) Find the negation of the following statements:
a) All fish can swim.
b) Today is not Friday.
c) It is not true that today is not a holiday.
3.) Let p=" I am a teacher" and let q="2+2=5"
a) I am not a teacher nor is 2=2+5.
b) If am not a teacher then 2+2  5.
5.
We can find the truth table for an entire compound statement.
| p | q | 
| 
|
| F | F | T | F |
| F | T | F | F |
| T | F | T | T |
| T | T | F | F |
Ex1: 
Definition: A compound statement that is always true, regardless of the truth values of its statement variables, is called a tautology. This statement is logically true.
Definition: A compound statement that is always false is called a contradiction. This statement is logically false.
Ex2:  is a tautology:
is a tautology:
| p | q | 
| 
|
| F | F | F | T |
| F | T | T | T |
| T | F | T | T |
| T | T | T | T |
A tautology is always true because of its logical structure and not because of the meaning of its individual simple statements.
Ex3:  is a contradiction.
is a contradiction.

| 
| 
| 
| 
|
| F | F | F | T | F |
| F | T | F | T | F |
| T | F | F | T | F |
| T | T | F | T | F |
It is always false because of its logical structure.
Theorem1: Let A and B be compound statements. If the compound statements A and A  B are tautologies then B is also tautology.
B are tautologies then B is also tautology.
Proof: (by method of contradiction).
Suppose that A and A  B are tautologies but B is not a tautology.
B are tautologies but B is not a tautology.
| A | B | A  B B
|
| F | F | T |
| F | T | T |
| T | F | F |
| T | T | T |
Note: A, B are compound statements so  and
and 
We assumed that B is not a tautology, so it is possible to assign some truth values to x, y, z, … so that  = F. We have to use the same values in
= F. We have to use the same values in 
Now for these values of x, y, z, …, A  B = T and B = F. It is possible only if A = F (see the table). But it contradicts to the initial condition that A is a tautology
B = T and B = F. It is possible only if A = F (see the table). But it contradicts to the initial condition that A is a tautology  These contradiction proves that our assumption (B is not a tautology) was wrong. End of proof.
These contradiction proves that our assumption (B is not a tautology) was wrong. End of proof.
If in a tautology we replace some statement variable by an arbitrary compound statement the resulting statement is also a tautology.
Ex: Given a tautology p˅~ p. We replace p by  We get a new tautology:
We get a new tautology:
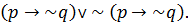
We can check it by making its truth table.
Ex: Given a tautology  . If we replace p by
. If we replace p by  we get a new tautology:
we get a new tautology:  .
.
H/a # 1: Prove that the statement  is tautology.
is tautology.
H/a #2: Use the result of the previous H/a to prove that the statement  is a tautology.
is a tautology.
H/a #3: Given a tautology 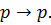 Prove that
Prove that  is a tautology.
is a tautology.
Date: 2015-12-11; view: 375; Нарушение авторских прав