Уравнения движения турбулентной атмосферы

Рассмотрим единичный объем воздуха, имеющий массу ρ. В об­щем случае на него действуют силы:

а) результирующая всех сил давления — градиент давления G; б) отклоняющая сила вращения Земли К; в) результирующая всех напряжений трения (молекуляр­ного и турбулентного) R; г) сила тяжести Р = pg. Если эти силы не уравновешиваются, то выделенный объем воздуха придет в движе­ние. По второму закону Ньютона произведение массы тела р на ускорение движения dc/dt равно сумме всех действующих на тело сил:

Это уравнение носит название уравнения движения атмосферы в векторной форме.

В метеорологии уравнения движения записывают обычно в ска­лярной форме. Прямоугольная (правая) система координат выби­рается так (см. рис. 19.1), чтобы плоскость хоу совпадала с горизон­тальной плоскостью, а ось оz — с вертикалью (положительное на­правление — вверх). Начало координат обычно помещается на уров­не моря.

Проектируя правую и левую части уравнения (19.2.1) последова­тельно на оси х, у, z, получаем с учетом результатов п. 19.1 систему уравнений движения атмосферы в координатной форме:

Систему уравнений (19.2.2) чаще всего записывают так, чтобы в левых частях стояли проекции ускорения. Для этого необходимо правую и левую части каждого уравнения последней системы разде­лить на плотность ρ. Третье уравнение движения, как показывает количественная оценка порядка величины различных членов, в бо­льшинстве случаев (но не во всех) сводится к основному уравнению статики.

В первых двух уравнениях системы (19.2.2) члены, содержащие вертикальную проекцию скорости, малы по сравнению с другими членами. Кроме того, часто пренебрегают изменением плотности с высотой. С учетом отмеченного запишем систему уравнений движе­ния атмосферы окончательно в следующем виде:

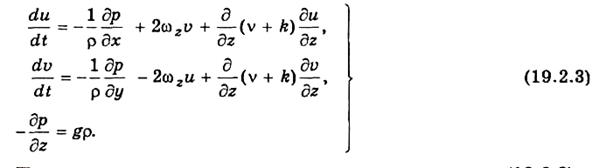
Подчеркнем, что производные в левых частях систем (19.2.2) и (19.2.3) представляют собой проекции ускорения движущегося объ­ема воздуха, т. е. являются индивидуальными производными от проекций скорости ветра по времени. Индивидуальные производ­ные записываются в виде

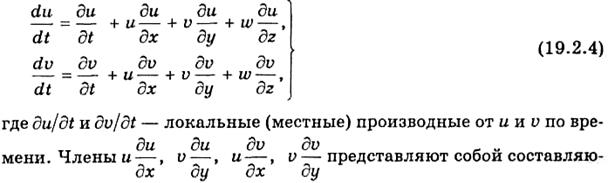
щие инерционной силы (в частном случае — центробежной силы). Подчеркнем, что и, v, w в (19.2.2), (19.2.3) и (19.2.4) представляют собой проекции средней скорости движения атмосферы (средней скорости ветра).

При изучении большинства явлений и процессов в метеорологии воздух рассматривается как идеальный газ, удовлетворяющий усло­вию сплошности среды. Это означает, что всякий малый объем (эле­мент) воздуха считается все же настолько большим, что содержит очень много молекул. Именно в таком смысле следует понимать вы­ражения „частица воздуха", „бесконечно малая частица", „элемен­тарный объем" и др. Для таких сплошных сред справедливо уравне­ние неразрывности, именуемое также уравнением сплошности сре­ды. Физически оно выражает факт неуничтожаемости массы жид­кости или газа (в нашем случае — воздуха).

Через единичную площадку (1 м²), перпендикулярную оси х, за единицу времени проходит масса воздуха, заключенная в объеме и · 1 м², т. е. равная ри. Поскольку, согласно определению, масса воз­духа, которая проходит через единичную площадку за 1с, представ­ляет собой поток массы, то приходим к заключению, что проекции этого потока на оси х, у, z равны

Дивергенция потока массы (взятая с обратным знаком):

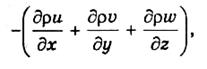
согласно теореме, доказанной в п. 9.4, равна притоку массы к еди­ничному объему за 1с. Приток же, в свою очередь, вызовет измене­ние массы единичного объема (которая равна р) во времени. За еди­ницу времени (1с) изменение массы равно dp/dt. Приравнивая изме­нение массы (dp/dt) к ее притоку

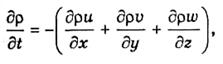
приходим к уравнению неразрывности, или сплошности среды:

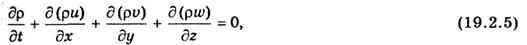
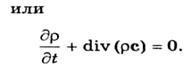
Выполнив дифференцирование произведений ри, ри, pw и вос­пользовавшись выражением для полной производной от р по t

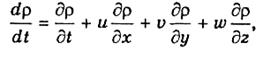
приходим ко второму виду уравнения неразрывности

:

Или

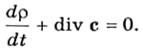
Полученные в этой главе уравнения движения атмосферы (19.2.3), уравнение неразрывности (19.2.5) вместе с выведенными в других главах уравнениями переноса тепла и влаги и уравнением состояния воздуха составляют систему основных уравнений метео­рологии, или (по предложению И. А. Кибеля) систему уравнений погоды. Дополнительными уравнениями метеорологии служат урав­нения переноса лучистой энергии, уравнение Клаузиуса—Клапей­рона и некоторые другие уравнения, которые привлекаются при ре­шении частных задач.

В общем случае система уравнений метеорологии исключитель­но сложна не только с точки зрения ее решения (эти трудности с по­мощью численных методов и вычислительной техники в настоящее время постепенно преодолеваются), но и с точки зрения физическо­го содержания (вида) отдельных членов этой системы.

При изучении конкретных атмосферных явлений и процессов система уравнений погоды всегда упрощается, в одних случаях до­статочно обоснованно, путем строгих оценок порядка величины от­дельных членов уравнений, в других — менее обоснованно, на осно­ве различных предположений.

Поскольку уравнения метеорологии являются дифференциаль­ными уравнениями в частных производных, для построения конк­ретного их решения необходимо задать начальное и граничные условия. Вид последних зависит от физического содержания изуча­емого явления или процесса.

Date: 2015-12-10; view: 1276; Нарушение авторских прав