Уравнение переноса водяного пара в турбулентной атмосфере

Водяной пар распространяется в атмосфере вследствие ее движе­ния, которое складывается из упорядоченного переноса со средней скоростью с (u, v, w) и турбулентных пульсаций. Молекулярная диффузия играет заметную роль лишь в непосредственной близости от испаряющей поверхности — вязком подслое толщиной в несколь­ко миллиметров.

Получим уравнение переноса водяного пара в турбулентной ат­мосфере. При движении индивидуальной частицы сохраняется по­стоянной (остается консервативной) массовая доля водяного пара. Все другие характеристики (абсолютная и относительная влаж­ность, давление, точка росы) при движении частицы изменяются. По этой причине турбулентный поток водяного пара, как уже ука­зывалось, пропорционален градиенту массовой доли водяного пара:

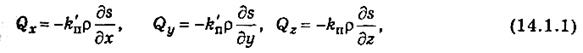
где k'_п и k_п — коэффициенты турбулентной диффузии водяного пара по горизонтали и вертикали (единица измерения — м²/с, как и в случае коэффициента турбулентности k). Обычно полагают, что эти коэффициенты равны (k _п = k), хотя некоторое различие между ни­ми, по-видимому, существует.

На основе уравнения (9.4.5), связывающего приток с потоком, можем записать следующее выражение для турбулентного притока (ε_п) водяного пара за 1 с к единичному объему:

Под влиянием этого притока происходит изменение доли водяного пара. Поскольку рассматривается движущийся индивидуальный объем воздуха, то изменение доли пара за единицу времени будет характеризовать полная производная (ds/dt); изменение же массы водяного пара в выделенном объеме составит

Приравнивая приток водяного пара под влиянием турбулентной диффузии к изменению массы его внутри выделенного объема воз­духа, получаем уравнение переноса водяного пара в турбулентной атмосфере

Если уравнение (14.1.4) разрешить относительно локальной произ­водной, то получим

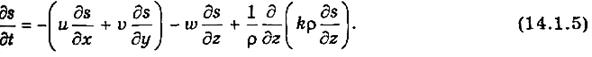
Здесь опущены члены с k '.

Согласно последнему уравнению, на изменение величины s в определенной точке пространства оказывают влияние следующие процессы.

1. Упорядоченный перенос водяного пара со средней скоростью в горизонтальном направлении. Этот процесс называют адвекцией во­дяного пара.

Под ее влиянием происходит увеличение массовой доли пара (ds/dt > 0), если воздух переносится из области с высоки­ми значениями s в область с относительно низкими s (направив ось х вдоль потока, получим: и > 0, v = 0, ds/dx < 0, а -uds/дх > 0). В том случае, когда в направлении переноса доля пара возрастает (ds/dx > 0), со временем под влиянием адвекции она уменьшается (ds/dt < 0).

2. Упорядоченный перенос пара вертикальными токами. Этот процесс называется конвекцией водяного пара. Если доля пара убы­вает с высотой (ds/dz < 0), что наиболее часто наблюдается в атмо­сфере, то при восходящем движении (w > 0) на фиксированном уровне влажность увеличивается со временем (ds/dt > 0), а при ни­сходящем (w < 0) уменьшается (ds/dt < 0).

3. Турбулентная диффузия пара в вертикальном и горизонталь­ном направлении. Диффузия всегда приводит к выравниванию доли пара, если не происходит притока или оттока водяного пара через границу области. Так, если в некотором слое доля пара в исходном
состоянии убывала с высотой, то под влиянием турбулентной диф­фузии произойдет увеличение s в верхней части слоя и уменьшение в нижней. Наиболее существенна роль диффузии в вертикальном направлении. Перенос и перераспределение пара по горизонтали
осуществляются в основном адвекцией. Турбулентная диффузия в этом процессе играет заметную роль лишь в тех областях, где резко изменяются свойства земной поверхности (например, вблизи бере­гов озер, морей и океанов).

Уравнение (14.1.5) — дифференциальное уравнение 2-го поряд­ка в частных производных. Для получения однозначного решения его необходимо задать граничные и начальное условия.

Начальное условие задается в виде известного (полученного, на­пример, из наблюдений) распределения в пространстве доли пара в исходный момент, от которого ведется отсчет времени. Граничные условия задаются в виде некоторых известных функций, которые описывают изменение доли пара во времени на границах области. За нижнюю границу наиболее часто принимается земная поверх­ность, за верхнюю — тропопауза или верхняя граница атмосферы (где поток водяного пара обращается в нуль).

Обычно принимается, что в непосредственной близости от вод­ной или сильно увлажненной поверхности водяной пар находится в насыщенном состоянии, т. е. s =sm(T₀, р₀). где Т₀ — температура водной поверхности, р₀ — давление воздуха вблизи нее.

Значительно труднее записать граничное условие на поверхно­сти суши. Только в том случае, когда поверхность суши сильно увлажнена, можно считать, что вблизи нее водяной пар находится в состоянии, близком к насыщению. Нередко в качестве граничного условия используется уравнение теплового баланса земной поверхности, в которое, наряду с радиационным балансом, входят потоки тепла в атмосферу и почву. По этой причине к системе уравнений переноса тепла и влаги в атмосфере присоединяются уравнения пе­реноса тепла и влаги в почве. Граничное условие в этом случае ста­вится на некоторой глубине, где температура постоянна (во време­ни), а влажность равна влажности насыщенного пара.

В заключение подчеркнем, что полученное в этом параграфе уравнение переноса водяного пара справедливо для ненасыщенного воздуха.

Date: 2015-12-10; view: 1465; Нарушение авторских прав