Силы, действующие в атмосфере

Силы давления. При наличии движения воздуха изобарические поверхности наклонены под некоторым углом а _p к уровенным по­верхностям. Нетрудно видеть (рис. 19.1), что результирующая всех сил давления, действующих на объем ABCD, по абсолютной величи­не равна

а по направлению совпадает с положительным направлением нор 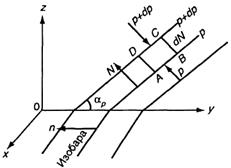мали к изобарическим повер­хностям. Поскольку объем ABCD, заключенный между изобарическими поверхностя­ми р и р + dp, равен dN, то мо­дуль результирующей сил давления, действующих на 1 м³ воздуха, равен

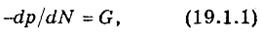
т. е., согласно п. 2 введения, представляет собой модуль градиента давления. Проекциями градиента давления G на оси (в метеороло­гии обычно правой системы) координат х, у и z служат (в соответст­вии с п. 2 введения)

Горизонтальная составляющая градиента давления G ₂ (ее мо­дуль G ₂ = - др/дп) служит единственной силой, под влиянием кото­рой возникает горизонтальное движение воздуха (ветер). Составля­ющую G ₂ часто называют барическим градиентом.

Отклоняющая сила вращения Земли — кориолисова сила. По­скольку атмосфера участвует в суточном вращении Земли с угловой скоростью ω, то на каждую частицу воздуха, движущуюся со скоро­стью с по отношению к земной поверхности, действует кориолисова сила. В общем случае кориолисова сила, действующая на 1 м³ воз­духа (на массу р), равна

где (с х ω) — векторное произведение векторов с и ω.

Если раскрыть по известным из векторного анализа правилам последнее произведение, то получим следующие выражения для проекций кориолисовой силы на оси х, y и z:

где и, v, w — проекции скорости ветра с; ω_x, ω_y, ω_z — проекции век­тора со на оси х, у и z соответственно.

Наибольший интерес представляет горизонтальная составляю­щая кориолисовой силы K s. В выражениях для проекций К х и К у составляющей K s можно пренебречь слагаемыми, содержащими вертикальную скорость ω, так как она в атмосфере в десятки—сот­ни раз меньше и и v. Таким образом, можно записать

где ω= ω sincφ — вертикальная проекция угловой скорости враще­ния Земли, φ — широта,

с = √u² +v².

При горизонтальном движении выражения для К х и К y будут точными. Исходя из соотношений (19.1.5) нетрудно показать, что горизонтальная составляющая К s кориолисовой силы действует под прямым углом к направлению движения: вправо — в северном полушарии и влево — в южном (рис. 19.2).

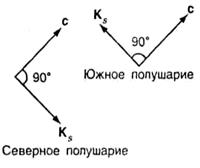
Чтобы убедиться в этом, достаточно горизонтальные оси координат выбрать так, чтобы ось х совпала с направлением скорости ветра. Тогда и = c >0, v = 0 и, как следует из

(19. 1.5), К х = 0,K y =- 2ω_zpc. Поскольку в северном полушарии пара­метр кориолиса 2ω_z > 0, а в южном 2ω_z < 0, то К у < 0 в северном полуша­рии и К у > 0 в южном, т. е. приходим к сформулированному выше утвержде­нию.

.

Силы трения (молекулярного и турбулентного). Трение прояв­ляется в жидкостях и газах в тех случаях, когда различные части их имеют разную скорость движения. В атмосфере наибольшее зна­чение имеют силы трения, порождаемые изменением скорости вет­ра с высотой, так как вертикальный градиент скорости ветра в де­сятки и сотни тысяч раз больше горизонтального: [ дс/дг ]»[ дс/дп ].

Пусть на уровнях z и z + dz скорости ветра равны соответственно с и с + dc. Молекулы воздуха, помимо поступательного движения со скоростью с + dc (на уровне z + dz), совершают хаотические тепло­вые движения. Приходя на уровень z, молекулы приносят импульс, которым они обладали на других уровнях. Соударяясь с молекула­ми, расположенными на уровне z, они будут сообщать им (или отни­мать у них) дополнительный импульс. Всякое же изменение импу­льса по второму закону Ньютона можно рассматривать как резуль­тат действия некоторой силы. Эта сила, отнесенная к единице по­верхности, называется напряжением молекулярного трения.

Обозначим через τ _м напряжение молекулярного трения, возни­кающее в результате воздействия вышележащих слоев на поверх­ность, расположенную на уровне z. Из качественных соображений очевидно, что напряжение трения должно быть пропорционально вертикальному градиенту скорости ветра:

де η — коэффициент пропорциональности, называемый динамиче­ским коэффициентом вязкости. Отношение η/ρ = v называется ки­нематическим коэффициентом вязкости. Величина η измеряется в кг/(с·м), a v — в м²/с, так как τ _м измеряется в Н/м².

Если движение имеет турбулентный характер, то обмен импуль­сом происходит благодаря перемещению не только молекул, но и значительно больших по массе частиц воздуха. В случае турбулент­ного потока мгновенная скорость отдельных частиц сильно изменя­ется (по абсолютной величине и по направлению) как во времени, так и при переходе от одной частицы к другой. Поэтому вводится понятие средней скорости потока (средней по времени или по неко­торому объему). Говоря в дальнейшем о распределении скорости ветра с высотой и об изменении ее во времени, всюду будем иметь в виду среднюю скорость с. Из таких же качественных соображений, которые были приведены при получении формулы для напряжения тм, следует, что напряжение турбулентного трения может быть за­писано в виде:

где А — коэффициент турбулентной вязкости (турбулентного обме­на), k — коэффициент турбулентности.

Коэффициент турбулентной вязкости в десятки и сотни тысяч (иногда миллионы) раз больше коэффициента молекулярной вязко­сти (А» η). По этой причине роль молекулярного трения везде мала по сравнению с турбулентным (за исключением очень тонкого вязкого подслоя, прилегающего к земной поверхности).

Для того чтобы подсчитать результирующую силу трения, дейст­вующую на выделенный объем воздуха, необходимо учесть влияние трения на этот объем со стороны как вышележащих, так и нижеле­жащих слоев атмосферы. Пусть для определенности выделенный объем воздуха имеет форму параллелепипеда с основанием 1 м² и высотой dz.

Обозначив через τ_zх проекцию напряжения трения τ_z на ось х на уровне нижнего основания и через τ_zх + dτ _zx — на уровне верхнего основания, найдем, что результирующая этих двух сил равна (на­пряжение трения на нижнем и верхнем основании направлено в противоположные стороны)

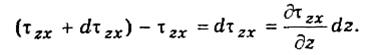
В общем случае напряжение трения представляет собой сумму напряжений молекулярного и турбулентного трения:

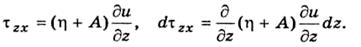
Такова проекция силы трения, действующей на объем dz.

Проекция силы трения, действующей на единичный объем воз­духа, равна

Аналогичное выражение получаем для проекции силы трения на ось и:

Количественные оценки показывают, что влияние шероховато­сти земной поверхности через молекулярный и турбулентный обмен сказывается в атмосфере до высоты от нескольких сотен метров до 1—1,5 км (в зависимости от шероховатости земной поверхности, термической стратификации, скорости ветра). Как было указано, этот слой, в котором наряду с градиентом давления и силой Кориолиса существенную роль играют силы турбулентного трения, носит название пограничного слоя атмосферы (рис. 19.3).

В свободной атмосфере турбулентный обмен (в смысле пульса­ций скорости ветра) выражен ничуть не слабее, чем в пограничном слое.

Однако роль трения в свободной атмосфере мала по сравнению 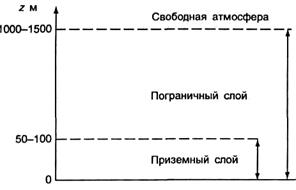с другими силами потому, что здесь малы вертикальные градиенты скорости ветра. В свободной атмосфере скорость ветра изменяется с высотой в основном под влиянием горизонтальной термической не­однородности (горизонтального градиента температуры). Велика роль сил трения в свободной атмосфере в области фронтальных зон, струйных течений и вообще в тех слоях, где градиент скорости вет­ра велик. В однородных воздушных массах в свободной атмосфере движение определяется в основном силами давления (барический градиент), силой Кориолиса и центробежной силой (при движении частиц по криволинейным траекториям).

Date: 2015-12-10; view: 1234; Нарушение авторских прав