Сухоадиабатический градиент

Исследуем вопрос об изменении температуры в адиабатически поднимающейся частице сухого воздуха. Для этого воспользуемся уравнением первого начала

и уравнением статики атмосферы, которое определяет изменение давления р = p_i = p_e с высотой:

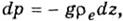
или

Последнее выражение dp/p подставим в уравнение (4.3.1). Тогда

Из этого уравнения, если разделить слагаемые на c_pdz, найдем, что изменение температуры воздушной частицы, отнесенное к еди­нице высоты, при адиабатическом процессе равно

Соотношение (4.3.3) показывает, что при адиабатическом подъе­ме воздушной частицы температура ее всегда понижается (dTi/dz < 0), что связано с расходом внутренней энергии на работу расширения.

Сухоадиабатическим градиентом называется понижение темпе­ратуры при адиабатическом подъеме сухой воздушной частицы, от­несенное к единице высоты:

Из сравнения (4.3.3) и (4.3.4) получаем

В общем случае, как показывает последнее соотношение, γ_а яв­ляется переменной величиной, зависящей от Т_i /Т_е. Но в реальной атмосфере различие в температурах воздушной частицы и окружа­ющей среды невелико (разность T_i - Т_е не превышает 5—10 °С). По этой причине отношение Т_i /Т_е можно считать близким к единице (Т_i /Т_е ≈ 1), а сухоадиабатический градиент — постоянной величи­ной:

Если воспользоваться соотношением (4.1.4), этой формуле мож­но придать другой вид:

Подставляя значения к, g и R_c, получаем:

Приближенно можно считать γ_а ≈ 1 ^oС/100 м, т. е. температура адиабатически поднимающейся сухой воздушной частицы понижа­ется примерно на 1 ^oС при подъеме на каждые 100 м высоты.

Как и введенные выше угловая скорость вращения (ω) и ускоре­ние свободного падения (g), сухоадиабатический градиент γ_а = g/c_p — постоянная величина только для данной планеты. Для сравнения приведем значения γ_а для некоторых планет Солнечной системы:

Если считать сухоадиабатический градиент постоянной величи­ной, то уравнение –dTi/dz = γ_а может быть проинтегрировано и за­писано в следующем виде:

где T_i0 и T_i — температура частицы соответственно на исходном уровне Z₀ и произвольной высоте z (в метрах). Последнее уравнение представляет собой приближенное уравнение сухой адиабаты.

Изменение с высотой температуры адиабатически поднимаю­щейся воздушной частицы графически изображается в осях коорди­нат температура — высота в виде прямой линии, которая носит на­звание сухой адиабаты, или кривой состояния сухой воздушной час­тицы.

Наряду с адиабатическими процессами, рассматриваются более общие, политропические. Политропическим процессом называется такой процесс, при котором приток тепла к воздушной частице пря­мо пропорционален изменению температуры:

где с — теплоемкость политропического процесса (величина посто­янная). Частными случаями политропического процесса являются адиабатический процесс (с = 0, dq = 0), изобарический процесс (с = с_р, dq = c_pdT), изостерический процесс (с =c_υ, dq = c_υdT), изотермический процесс (с = ± ∞, dT = 0).

Date: 2015-12-10; view: 1054; Нарушение авторских прав