Вертикальный масштаб атмосферы

Барометрические формулы широко используются, в частности, при изучении свойств верхних слоев атмосферы (термосферы и экзосферы) с помощью ИСЗ, космических кораблей и ракет. Отметим, что атмосфера и на больших высотах оказывает существенное влия­ние на летательные аппараты при их длительном пребывании в ней: под влиянием силы сопротивления происходит постепенное умень­шение полной механической энергии спутника и, следовательно, изменение элементов орбиты. Сила сопротивления и скорость изме­нения элементов орбиты спутника прямо пропорциональны плотно­сти воздуха на высоте полета. При облете Земли спутник проходит через слои атмосферы с различной плотностью. Для оценки влия­ния атмосферы на изменение элементов орбиты за полный оборот необходимо знать зависимость плотности воздуха от высоты. Выве­дем формулы для распределения давления и плотности воздуха по высоте в верхних слоях атмосферы, которые обобщают формулы п. 3.3. Необходимость такого обобщения диктуется тем, что в верх­них слоях атмосферы изменяется с высотой не только температура, но и молекулярная масса (состав воздуха). Ускорение свободного па­дения при изменении высоты в широких пределах также нельзя принимать за постоянную величину.

Если, как и в п. 3.3, в основном уравнении статики (3.2.4) плот­ность воздуха заменить по уравнению состояния (1.4.8), то полу­чим:

При последнем переходе R заменено на R*/μ. (здесь R* — универ­сальная газовая постоянная, μ — относительная молекулярная мас­са воздуха).

Одно из важнейших свойств уравнений заключается в том, что размерности их левой и правой части должны быть одинаковыми. Левая часть (3.5.1) безразмерная. Следовательно, и правая часть должна быть безразмерной. Однако множитель dz в правой части имеет размерность длины. Таким образом, приходим к заключению о том, что вошедшая в правую часть (3.5.1) величина

также имеет размерность длины; в этом можно убедиться и путем непосредственной проверки. Параметр Н, объединяющий три пере­менные величины (T, μ, g), называют высотой однородной атмосфе­ры или вертикальным масштабом атмосферы. После введения Н основное уравнение статики принимает следующий вид:

По своему физическому смыслу параметр Н совпадает с введен­ной в п. 3.2 высотой однородной атмосферы. Различие состоит в том, что в п. 3.2 в выражение для Н входила температура у земной поверхности, в то время как в формулу (3.5.2) входит температура на произвольной высоте. Но во всех случаях Н — это толщина та­кой однородной атмосферы, у которой давление и плотность на ее нижней границе равны давлению и плотности на том уровне в ре­альной атмосфере, для которого по формуле (3.5.2) рассчитан пара­метр Н. Чтобы убедиться в этом, достаточно обратиться к формуле (3.2.7). Пусть на каком-либо фиксированном уровне z₁ давление бу­дет p₁, плотность ρ₁ и температура Т₁. Тогда, согласно (3.2.7) и определению толщины H₁ однородной атмосферы, в которой (на всех высотах) плотность равна ρ₁(можем записать

Пренебрегая зависимостью g от z, получаем: p₁ = gρ₁H₁, т. е.

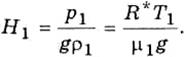
Эта формула совпадает с формулой (3.5.2), хотя получена она на основе представления об Н как о толщине однородной атмосферы.

Параметр Н можно ввести также и в уравнение состояния воз­духа:

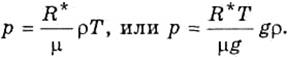
Отсюда

Подчеркнем, что с введением параметра Н, объединяющего три переменные величины (T, μ, g), при получении барометрических формул отпадает необходимость раздельного учета изменения каж­дой из этих величин (в частности, g) с высотой. Формула (3.5.3) по­казывает, что изменение давления обусловливается распределением по высоте именно Н, а не каждой из трех переменных величин в от­дельности.

В общем случае Н является достаточно сложной функцией высо­ты; выше 95—100 км изменяются с высотой не только Т и g, но и μ. Если в некотором слое параметр Н считать постоянным (Н = const), то, интегрируя уравнение (3.5.3), получим барометрическую формулу для такого слоя в виде

где z_π — высота нижней границы слоя, р_π — давление воздуха на этой границе. Именно в таком виде чаще всего используется баро­метрическая формула при решении задач о влиянии атмосферы на изменение элементов орбиты, а также на время существования ИСЗ и других летательных аппаратов. В качестве нижней границы z_π в этих случаях берется высота перигея спутника.

Если уравнение состояния (3.5.4) записать для уровня z_π:

то после деления (3.5.4) на (3.5.6) с учетом формулы (3.5.5), получа­ем формулу для плотности воздуха в слое с Н = const:

Обычно изменением g с высотой пренебрегают, полагая в послед­ней формуле g_π/g ≈ 1.

Date: 2015-12-10; view: 976; Нарушение авторских прав