Барометрические формулы

Уравнение статики является одним из важнейших уравнений метеорологии, на основе которого устанавливаются закономерности распределения давления, плотности и массы воздуха по высоте. В своем дифференциальном виде уравнение статики (3.2.4) позволяет выполнить расчет изменения давления лишь для малых прираще­ний высоты dz.

На практике всегда необходимо иметь данные о распределении давления в слоях атмосферы конечной толщины или определить толщину таких слоев по измеренным значениям давления. Для этой цели уравнение статики следует записать в конечном (интеграль­ном) виде, т. е. найти его интегралы. Интегралы уравнения статики атмосферы, полученные при разных предположениях относительно изменения температуры и плотности воздуха с высотой, носят об­щее название барометрических формул. На основе барометриче­ских формул решаются такие важные практические задачи, как расчет распределения давления и плотности по высоте, определение высоты различных летательных аппаратов по измеренному давле­нию, приведение давления к уровню моря и др.

Для получения интегральной формы уравнения статики проин­тегрируем левую и правую части (3.2.4) в пределах от уровня моря 2=0 (или земной поверхности), где давление р0, до произвольной высоты г, где давление р. Имеем

Откуда

Здесь ρ = ρ(z) – функция высоты

Другую интегральную форму уравнению статики можно при­дать, если воспользоваться уравнением состояния влажного воздуха (1.4.12) из главы 1. Подставив найденное отсюда значение р, пере­пишем (3.2.4) в виде

.

Интегрируя в пределах от 0 до z и от р₀ до р, получаем:

Интегральные формы (3.3.1) и (3.3.3) уравнения статики в даль­нейшем широко используются для получения различных баромет­рических формул. Заметим, что p₀ в формулах (3.3.1) и (3.3.3) может обозначать давление как на уровне моря, так и на поверхности Земли. Различие будет состоять лишь в начале отсчета высоты г. В общем случае температура, а вместе с ней и плотность воздуха явля­ются достаточно сложными функциями высоты, установить анали­тический вид которых не всегда представляется возможным. Поэто­му прежде чем перейти к общему случаю, рассмотрим несколько ча­стных случаев, отличающихся один от другого различными предпо­ложениями относительно вида функций Т = T(z) или р = р(z), с по­мощью которых описывается распределение температуры или плот­ности по высоте.

Однородная атмосфера. Предположим, что плотность воздуха в пределах всей атмосферы

не изменяется с высотой, т. е.

Здесь р₀— плотность воздуха при z = 0. Такая атмосфера носит на­звание однородной. Пренебрежем зависимостью ускорения свобод­ного падения от высоты. Тогда на основании (3.3.1) получаем баро­метрическую формулу однородной атмосферы:

Согласно этой формуле, давление в однородной атмосфере убывает с высотой по линейному закону (рис. 3.2).

Отметим, что в приложении к атмо­сфере формула (3.3.5) дает заведомо дале­кое от реальных условий распределение давления. Однако для гидросферы, плот­ность которой изменяется в очень узких пределах (плотность воды близка к 1 г/см3), формула (3.3.5) дает вполне удовлетворительные результаты. Поэтому ее можно назвать барометрической фор­мулой гидросферы (высота в этом случае отсчитывается от дна моря или океана).

Поставим вопрос о высоте однородной атмосферы, т. е. такой высоте, на которой давление обращается в нуль (р = 0).

Обо­значим ее через Н. Согласно (3.3.5), имеем

Поскольку в соответствии с уравнением (1.3.8) р₀/ρ₀ = R_cT₀ (T₀— температура воздуха при z = 0), формула (3.3.6) принимает вид

Отсюда следует, что высота однородной атмосферы конечна и зави­сит только от

температуры воздуха на поверхности Земли. При Т = О °С она составляет

Поскольку плотность в однородной атмосфере постоянна, а дав­ление быстро убывает с высотой, температура ее, равная в соответ­ствии с уравнением состояния

должна понижаться. Если взять производную по высоте от левой и правой части (3.3.8), то получим:

Привлекая (3.2.5), находим следующее выражение для верти­кального градиента температуры

у_А в однородной атмосфере:

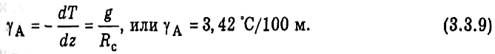
Таким образом, в однородной атмосфере температура убывает с высотой по линейному закону:

при этом скорость понижения температуры (градиент) значительно больше среднего значения у в пределах тропосферы.

Изменение плотности воздуха с высотой. Рассмотрим вопрос об изменении плотности воздуха с высотой в общем случае. С этой целью сначала прологарифмируем, а затем продифференцируем по высоте левую и правую часть уравнения состояния (1.3.8):

Заменив dp/dz в соответствии с (3.2.5) и подставив в полученное выражение р из уравнения (1.3.8), найдем:

Формула (3.3.11) справедлива для любого распределения темпе­ратуры воздуха по высоте. На основе ее можно сделать выводы отно­сительно изменения плотности воздуха с высотой. Возможны три различных случая.

1. Если γ > γ_А= 3,42 ^oС/100 м, то dρ/dz > 0, т. е. плотность возду­ха возрастает с высотой. Вертикальные градиенты температуры γ, превышающие 3,42 ^oС/100 м, в реальных условиях атмосферы мо­гут наблюдаться лишь в дневные часы (летом) в приземном слое ат­мосферы. При таких условиях плотность в этом слое увеличиваетсяс высотой.

2. Если γ = γ_А, то dρ/dz = 0, т. е. плотность воздуха не изменяет­ся с высотой (постоянна): ρ = ρ₀ = const. Это случай однородной ат­мосферы.

3. Если γ < γ_А, то dρ/dz < 0, т. е. плотность воздуха убывает с высотой. Этот случай является абсолютно преобладающим в услови­ях атмосферы. Прежде всего, выше приземного слоя γ < γ_А при лю­бых состояниях атмосферы. В приземном слое случаи γ < γ_А наблю­даются также значительно чаще, чем случаи γ > γ_А. Таким образом, наиболее характерным состоянием атмосферы является такое, ког­да плотность воздуха убывает с высотой.

Изотермическая атмосфера. Атмосфера называется изотерми­ческой, если температура не изменяется с высотой, т. е.

Т = То = const,

где То — температура на уровне моря или поверхности Земли. Изо­термическая атмосфера по своим свойствам во многом противопо­ложна однородной атмосфере. Считая атмосферу сухой и пренебре­гая зависимостью ускорения свободного падения от высоты, на основании (3.3.3) и последнего соотношения получаем барометриче­скую формулу изотермической атмосферы:

Давление в изотермической атмосфере убывает с высотой по экс­поненциальному (показательному) закону

Графически зависимость давления р от высоты z в изотермиче­ской атмосфере представлена на рис. 3.3. Рисунок 3.3 а поясняет вытекающую из формулы (3.3.12) закономерность: если высота воз­растает в прогрессии арифметической, то давление убывает в про­грессии геометрической. Кривые на рис. 3.3 б соответствуют раз­личным температурам атмосферы (постоянным по высоте): T^′′₀ > T^′₀. Из этого рисунка и анализа формулы (3.3.12) следует, что при од­ном и том же давлении у земной поверхности давление на высотах (например 5, 10, 15 км) при температуре T^′′₀ больше, чем при T^′₀. Одно и то же значение давления наблюдается при температуре T^′′₀ на более высоких уровнях, чем при температуре T^′₀. Это означает, что при более высокой температуре давление в изотермической атмо­сфере убывает с высотой медленнее, чем при более низкой темпе­ратуре.

Абсолютное значение убывания давления в слоях равной толщи­ны в нижней части атмосферы больше, чем в верхней. Так, в слое от О до 5 км давление при средних условиях падает на p₀ - p₀/2 = p₀/2, т. е. примерно на 500 гПа (при р₀ = 1000 гПа); в слое от 5 до 10 км падение давления составляет р₀/2 - р₀/4 = р₀/4 т. е. около 250 гПа, а в слое от 20 до 25 км давление уменьшается всего лишь на р₀/16 - р₀/32 = р₀/32, т. е. примерно на 31—32 гПа. Таким образом, чем выше расположен слой атмосферы определен­ной толщины, тем меньше падение давления в этом слое.

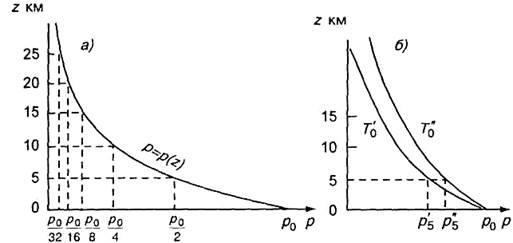
Рис. 3.3. Распределение давления по высоте в изотермической атмосфере.

а — общая закономерность падения давления, б — падение давления при разных темпе­ратурах (T^′′₀ > T^′₀).

Высота изотермической атмосферы равна бесконечности, т. е. р → 0 только при z → ∞.

Формула для плотности воздуха может быть получена, если обратиться к уравнению состояния, согласно которому

Поскольку в изотермической атмосфере Т/Т₀ =1, то на основа­нии (3.3.12) получаем

Величина δ = ρ/ρо носит название относительной плотности.

Политропная атмосфера. Политропной называют такую атмо­сферу, которая характеризуется линейным изменением температу­ры с высотой (или постоянным значением вертикального градиента температуры):

Считая атмосферу сухой (T_υ = Т) и подставляя Т в соответствии с (3.3.14) в формулу (3.3.3), получаем:

Выполнив интегрирование (в предположении g — const), прихо­дим к барометрической формуле политропной атмосферы:

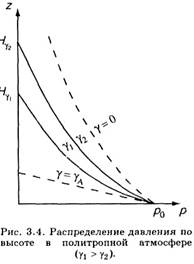
Графически зависимость р от z изображена на рис. 3.4. Кривые соответствуют одним и тем же значениям р₀ и T₀, но различным значениям вертикального градиента температуры: γ₁ и γ₂. Давле­ние при большем значении вертикального градиента температуры (γ₁) убывает с высотой быстрее, чем при меньшем (γ₂). Для сравне­ния на рис. 3.4 приведены кривые изменения давления в однород­ной и изотермической атмосферах (штриховые кривые). Высота по­литропной атмосферы конечна. В самом деле, согласно (3.3.15), дав­ление обращается в нуль на такой высоте z = Н_γ, на которой

Высота политропной атмосферы изменяется в широких пределах; при Т₀ = 288 К и γ = 0,65 К/100 м значе­ние Нγ составляет 44,3 км.

Формула для плотности воздуха в политропной атмосфере имеет вид

Полная барометрическая форму­ла (формула Лапласа).

Рассмотрим общий случай, т. е. случай произ­вольного распределения температуры по высоте. Учтем также, что реаль­ный воздух влажный, а ускорение свободного падения — функция ши­роты и высоты. Привлекая соотноше­ние (3.1.2) и учитывая, что

уравнение (3.3.2) перепишем в виде

Поскольку

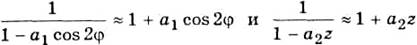
(вследствие малости слагаемых а₁ cos 2φ> и a₂z по сравнению с едини­цей), то формулу (3.3.18) приведем к виду

где H₀ = 273R_c/g₀ — высота однородной атмосферы при t = 0 °С.

Проинтегрируем (3.3.19) в пределах от высоты z₁, где давление равно p₁, до высоты z₂, где давление равно р₂. Для величин t, s и z в правой части (3.3.19) при интегрировании введем средние значения (на основании известной теоремы о среднем). Выполнив интегрирование, получим:

Поскольку

полная барометрическая формула (формула Лапласа) окончательно принимает вид

Величина В = 2,30Н₀ ≈ 18 400 м называется барометрической постоянной, а средние значения и носят название средних баро­метрических (температуры и доли водяного пара соответственно).

В таком полном виде барометрическая формула на практике ис­пользуется лишь при барометрическом нивелировании. При реше­нии подавляющего большинства метеорологических задач такой высокой точности, какую может обеспечить формула Лапласа, не требуется. К тому же следует иметь в виду, что точность измерения исходных данных (температуры, влажности, давления), необходи­мых для выполнения расчетов по формуле (3.3.21), как правило, значительно меньше тех уточнений, которые дает формула Лапласа по сравнению с приводимой ниже барометрической формулой ре­альной атмосферы. Последняя получается из формулы (3.3.21), если считать воздух сухим (s = 0) и пренебречь зависимостью уско­рения свободного падения от широты и высоты:

Возвращаясь к натуральным логарифмам и абсолютной темпера­туре, формулу (3.3.22) можно переписать в виде

где = 273(1 + a ) — средняя барометрическая температура слоя воздуха, заключенного между уровнями z₁ и z₂. Из сравнения по­следней формулы с формулой (3.3.3) следует, что средняя барометрическая температура связана с температурой воздуха следующим образом:

Средняя барометрическая температура — это такая постоянная в пределах слоя температура, которая обеспечивает значения давле­ния на границах его, наблюдаемые при реальном распределении температуры по высоте. Практически Т нередко отождествляют со средней арифметической температурой, т. е. полагают

где Т₁ и Т₂ — температуры воздуха на нижней и верхней границах слоя. Если уровень z₁ совпадает с поверхностью Земли (z₁ = 0), а уровень z₂ — произвольный (z₂ = z), то формула (3.3.23) принимает вид

Эта формула имеет такой же вид, как и барометрическая форму­ла (3.3.12) изотермической атмосферы. Принципиальное различие состоит в том, что формулы (3.3.20), (3.3.23) и (3.3.25) всегда спра­ведливы лишь для слоя заданной конечной толщины, для которого температура должна быть каждый раз определена прежде, чем по формулам можно начинать выполнять расчет. Вместе с изменением толщины слоя изменяется и величина . В случае же изотермиче­ской атмосферы температура является независимой (задаваемой) величиной. Поскольку барометрическая формула реальной атмо­сферы является показательной функцией, на основе ее анализа можно сделать такие же выводы относительно закономерностей из­менения давления с высотой, какие были сделаны в случае изотер­мической атмосферы. Роль температуры T₀ в реальной атмосфере играет средняя барометрическая температура . Все выводы в слу­чае реальной атмосферы относятся к слою конечной толщины. Поэ­тому вывод о бесконечной протяженности атмосферы, сделанный на основе формулы (3.3.12), здесь отпадает.

Если необходимо учесть влияние влажности на плотность возду­ха и распределение давления по высоте, то в формулах (3.3.22) — (3.3.25) средняя барометрическая температура должна быть заме­нена средней виртуальной барометрической температурой _υ.

Date: 2015-12-10; view: 5061; Нарушение авторских прав