Динамика атмосферы

В атмосфере постоянно наблюдаются движения воздуха. Непосредственной причиной их служит неравномерное распределение давления, обусловленное в свою очередь неоднородностью поля температуры. Каковы же силы вызывающие эти движения:

3.1 Силы, действующие в атмосфере.

Силы, действующие в атмосфере можно разделить на 2 группы: массовые и поверхностные. Массовые – это силы, которые действуют на каждый элемент массы (объема) независимо от того, существуют ли рядом другие воздушные частицы. Такими силами являются: сила тяжести, отклоняющая сила вращения Земли, центробежная сила. Поверхностные силы представляют собой силы взаимодействия некоторого объема воздуха и окружающей среды. Это сила барического градиента и вязкие силы.

3.1.1. Сила тяжести (g). Это равнодействующая силы притяжения к центру Земли (F) и центробежной силе (С), направленной по радиусу вращения. Сила тяготения (притяжения) равна: 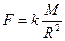, где k – гравитационная посеянная, равная 6,67*10^-8см³*г^-*с^-2; М – масса Земли; R – радиус Земли. Центробежная сила С = 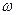²*R*Cos²φ, где 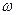= 7,29*10^-5с – угловая скорость вращения Земли; φ – географическая широта; R – радиус Земли. Следовательно 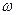²*R*Cos²φ. Из формулы видно, что g увеличивается по направлению к полюсам, т.к. в этом направлении увеличивается F(за счет уменьшения R) и уменьшается С (за счет широты). Однако вклад в «g» центробежной силы составляет всего 1/280. Таким образом, сила тяжести приводит к тому, что тело падает вниз по отвесной линии с ускорением свободного падения. Это ускорение на φ = 45⁰ составляет g = 9,8 м/с² (на уровне моря).

3.1.2. Отклоняющаяся сила вращения Земли (сила Кориолиса).

В механике доказывается, что при движении любого тела (в том числе воздуха) относительно вращающейся Земли оно отклоняется от первоначального направления вправо в северном полушарии и влево – в южном, сила направлена под углом 90⁰ к скорости. Она не меняет модуль 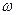, а лишь меняет направление. Причина возникновения силы заключается в том, что тело сохраняет свое направление движения, а суточное вращение Земли изменяет направление меридианов и параллелей. Поэтому с Земли кажется, что тела откланяются от направления меридианов и параллелей. Горизонтальная составляющая силы Кориолиса равна A = 2 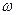*v*Sinφ, где v – скорость движения тела. Следовательно эта сила увеличивается по направлению к полюсам (за счет Sin φ) и с увеличением скорости v. На экваторе она равна 0.

3.1.3 Сила барического градиента.

В атмосфера почти всегда наблюдаются горизонтальные градиенты атмосферного давления. При этом воздух стремится перемещаться из мест с более высоким давлением в места с более низким давлением. Мерой неравномерности давления является горизонтальный барический градиент (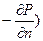. Поэтому чем больше барический градиент, тем интенсивнее движение воздуха. Если барический градиент отнести к единице массы, т.е. 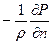, то по смыслу (и по размерности) это выражение является ускорением или силой, отнесенной к ед. массы. По направлению эта сила в каждой точке барического поля совпадает с нормалью к изобаре в сторону убывания давления. Сила барического градиента является единственной силой, которая вызывает движение воздуха. Все другие силы могут лишь тормозить движение или отклонять его от направления градиента.

Если бы на воздух действовало только ускорение, которое получает воздух под действием барического градиента, то движение воздуха постоянно бы ускорялось. Однако в действительности скорость ветра не может превышать нескольких десятков м/с. Из этого следует, что кроме силы барического градиента на воздух действуют другие силы, которые уравновешивают силу градиента.

3.1.4. Сила трения

Сила трения в атмосфере возникает, когда объемы (слои) движущегося воздуха имеют разные скорости. Между слоями воздуха имеет место определенная вязкость, которая препятствует скольжению их относительно друг друга. Поэтому чем больше скорость воздуха (их разности), тем больше сила трения или R = -kv (где k – коэффициент трения), тем сильнее затормаживается движение и изменяется его направление.

Природа вязкости между слоями воздуха двоякая: она молекулярная и турбулентная. Однако расчеты показывают, что коэффициент турбулентной вязкости на несколько порядков больше молекулярного. В связи с этим молекулярной вязкостью можно пренебречь. Тогда , где R – сила трения; p – плотность воздуха; τ – касательное напряжение внутреннего трения; z – направление движения воздуха (перпендикулярно к стенке).

С высотой влияние трения в атмосфере быстро уменьшается. И на уровне 1000-1500 м оно практически исчезает. Эта высота потому называется уровнем трения, а стой атмосферы – слоем трения (пограничным слоем).

При неустойчивой атмосфере уровень трения выше, чем при устойчивой.

3.1.5. Центробежная сила. Она возникает в том случае, если движение воздуха происходит по криволинейной траектории. В этом случае она равна: с = v²/r, где v – скорость движения; r – радиус кривизны движения. Для атмосферных движений с обычно мала, т.к. велико значение r.

3.1.6. Уравнение движения

Таким образом в атмосфере на объем воздуха действуют выше названные силы. Уравнение движения в общем виде будет иметь вид:

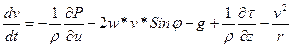
3.1.7. Геострофический ветер, его изменения с высотой

Рассмотрим один из частных случаев движения воздуха в атмосфере. Пусть частица воздуха, имеющая единицу массы, попала в атмосферу. При этом трение отсутствует и мы рассматриваем горизонтальное движение. Тогда под действием силы градиента давления частица начнет двигаться от высокого давления к низкому вдоль нормали к изобаре. Но как только она начнет двигаться на нее начнет действовать сила Кориолиса, которая будет отклонять движение частицы вправо от направления под прямым углом. В конце-концов, когда эти две силы уравновесятся частица будет совершать прямолинейное равномерное движение.

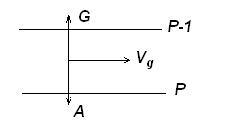
Такое движение называется геострофическим ветром.

Математически такое движение можно описать так. , где G – сила барического градиента; А – сила Кориолиса. Или 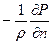= 2 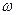*v_g*Sinφ, отсюда .

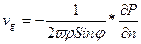Таким образом, геострофический ветер пропорционален градиенту давления и обратно пропорционален широте. На экваторе он не существует (т.к. = бесконечности). Для стандартных условий (t = 0⁰C, P = 1000гПа): , где ∆P/∆n – в гПа на 100км, v_g – в м/с.

Т.к. при геострофическом ветре сила трения не принимается во внимание, то такой ветер может наблюдаться лишь выше слоя трения, т.е. выше 1-1,5 км. С высотой из-за уменьшения ρ геострофический ветер усиливается.

Более общим случаем движения воздуха без трения является градиентное в поле криволинейных изобар (циклон, антициклон). В этом случае в уравнении движения входит помимо силы барического градиента и силы Кориолиса еще третья сила – центробежная, т.е. 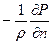- 2 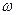*v*Sinφ - 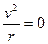; или
v_гр = - 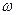*r*Sinφ + - для циклона.

Графически градиентный ветер можно изобразить следующим образом:

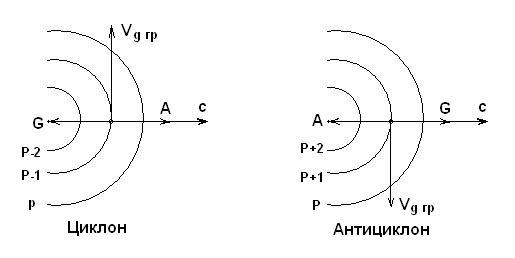
Здесь в циклоне силу барического градиента уравновешивают 2 силы А и С. Градиентный ветер направляется вправо под прямым углом к градиенту.

В антициклоне сила Кориолиса уравновешивается G и С.

В обоих случаях градиентный ветер направлен по касательной к изобаре вправо от барического градиента.

Расчеты градиентного ветра (v_гр) можно выразить через геострофический:

V_{гр.циклон} = v_g - ; V_{гр.антициклон} = v_g + .

У земной поверхности воздух испытывает трение при движении относительно Земли. Особенно заметно влияние поверхности примерно до высот 50-100 м над Землей. Этот слой называется приземным (до 1-1,5 км – пограничный). В этом слое при формировании ветра необходимо учитывать силу трения, которая тормозит движение и меняет его направление. Рассмотрим схему соотношения сил в атмосфере в этом случае. В случае прямолинейных изобар барический градиент направлен перпендикулярно изобарам (G); ветер v и его направление уже будет дуть не вдоль изобар, а под острым углом от силы барического градиента α (вправо). Сила трения R направлена в противоположную сторону движения воздуха. А уравновешивать силу барического градиента должны 2 силы: сила Кориолиса А и сила трения (А+R). Тогда из построения прямоугольника и учитывая, что сила А направлена под прямым углом к v и в право от него, находим положение силы Кориолиса.

Для определения скорости реального ветра нужно составить уравнение, где сумма трех сил равна нулю: G+A+R=0, подставив выражение для каждой силы, можно прийти к выражению для v: v = * , где k – коэффициент трения. Следовательно скорость ветра у Земли пропорциональна барическому градиенту и обратно пропорциональна коэффициенту трения и широте. Угол α между ветром и барическим градиентом составляет в умеренных широтах 60-75⁰ над океанами и 40-50⁰ – над сушей.

При круговых изобарах, т.е. в циклонах и антициклонах у Земли следует учитывать еще и центробежную силу С. Схема направления движения в этих случаях будет:

С высотой в слое трения скорость ветра растет, а направление приближается к изобаре (слева низкое давление). Изменение ветра с высотой в слое трения можно представить годографом, т.е. кривой которая еще называется спиралью Экмана. То ветер с высотой как бы вращается вправо.

В слое трения у поверхности обнаруживается суточный ход ветра, с max в 14 часов, min ночью или утром. Начиная примерно с высоты 500 м суточный ход обратный – max ночью, min днем. Такой суточный ход объясняется суточным ходом турбулентного обмена. Днем турбулентность max, поэтому сверху к поверхности опускаются вихри с повышенной скоростью, а снизу вверх – с пониженной. Поэтому днем внизу max, а вверху min скорости. Ночью внизу min интенсивности турбулентности, а вверху, поэтому, вихри с повышенной скоростью остаются там и скорости здесь достигают max.

3.1.9. Местные ветры (самостоятельная работа)

Date: 2015-12-10; view: 1117; Нарушение авторских прав