Метод сил

Канонические уравнения метода сил в матричной форме имеют вид

(2.5)

где матрица единичных перемещений 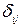- перемещение по направлению неизвестного X_i от действия неизвестных X_j = 1, 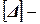матрица перемещений по направле­нию неизвестных в основной системе от заданной нагрузки:

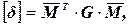
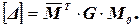(2.6)

В формулах (2.6) принято матрица изгибающих моментов в основной системе метода сил, 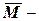матрица единичных изгибающих моментов от X=1, G – матрица податливости.

Из (2.5), (2.6) находим неизвестные

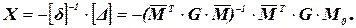(2.7)

Расчетные изгибающие моменты определяются следующим образом

или с учетом (2.7)

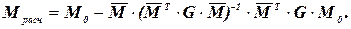(2.8)

Несложные преобразования приводят к формулам

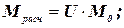(2.9) 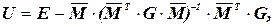(2.10)

где U – матрица раскрытия статической неопределимости.

Для проверок расчетов выполняемых по формулам (2.6) – (2.10) вы­полняются универсальные проверки коэффициентов канонических урав­нений

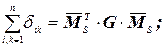
После определения M_расч выполняется деформационная проверка

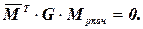(2.11)

В случае выполнения проверки (2.11) с точностью не хуже 3% строим эпюру Q, используя дифференциальные зависимости при изгибе

что для случаев действия на участки рамы равномерно распределенной нагрузки интенсивности q приводит к простой формуле

(2.12)

где - значения перерезывающей силы на левом и на правом концах

уча­стка, l_уч - длина участка, М_прав, М_лев изгибающие моменты на правом и ле­вом концах участка.

После построения эпюры Q_расч вырезаем жесткие узлы рамы, показы­ваем внутренние и внешние силы, действующие на них, из уравнений равновесия узлов определяем нормальные силы на участках рамы, при­мыкающих к рассматриваемому узлу.

Пример №12. Построить эпюры изгибающих моментов, перерезываю­щих и нормальных сил для рамы, показанной на Рис.2.7. Ко­личество неизвестных n=3k-ш=3*2-4=2. Выбираем основную систему, от­бросив две лишних связи, заменив их действие неизвестными X₁, X₂ (Рис.2.8).

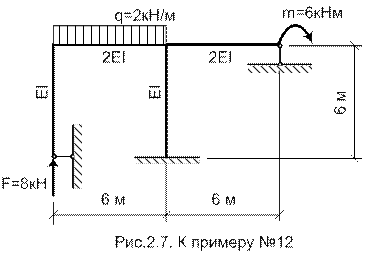
Строим эпюру изгибающих моментов в основной системе от задан­ной нагрузки: Эп.M_F, и эпюры изгибающих моментов от X₁=1, X₂=1: Эп.М₁ и Эп.М₂. Строим суммарную единичную эпюру от совместного действия X₁=X₂=1 (Рис.2.9). Составляем грузовую матрицу , единичные матрицы , и матрицу податливости G:

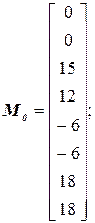
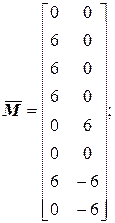
Перемножим матрицы

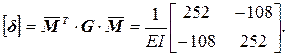
Универсальные проверки:

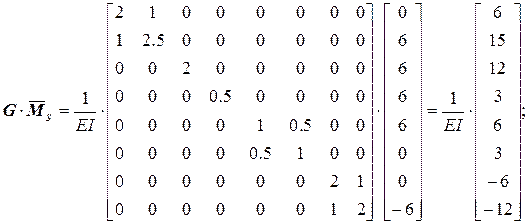
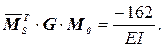
выполнены, так как , .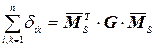

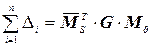Определитель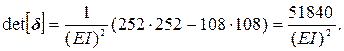

Алгебраические дополнения:

, .

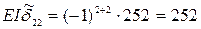Обратная матрица .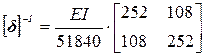

Неизвестные

Расчетная эпюра изгибающих моментов

Деформационная проверка

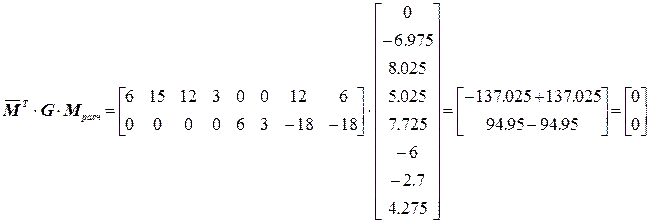Используя (2.12), строим расчетную эпюру перерезывающих сил. Выре­заем жесткие узлы рамы, составляем уравнения равновесия для них, из которых определяем нормальные силы в элементах рамы. Строим рас­четную эпюру нормальных сил (Рис.2.11).

С помощью построенных эпюр определяем реакции в заданной раме. Изображаем раму с внешними нагрузками и опорными реакциями (Рис.2.12). Состав­ляем уравнения равновесия полученной системы сил.

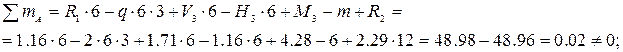
Уравнения равновесия выполняются с высокой точностью.

Date: 2015-12-10; view: 1173; Нарушение авторских прав