Матричная форма определения перемещений

Для определения перемещений применяется формула Мора:

, (2.1)

где - единичное внутреннее усилие по направлению искомого перемеще­ния; - внутреннее усилие от заданной нагрузки; - жесткость поперечного сечения для данного вида деформаций.

Для вычисления интеграла (2.1) используем формулу трапеций при аппроксимации подинтегральных функций прямыми линиями, или фор­мулу Симпсона при аппроксимации линейной функцией, а квадрат­ной параболой, в обоих случаях считаем постоянной на всем участке.

Рассмотрим участок длиной , жесткостью , внутренние усилия на концах эпюры равны a, b и c, d на концах эпюры , и e, f в серединах уча­стков тех же эпюр. Перемножаем эпюры M_i и M_k по правилу Верещагина:

Учитываем, что

Полученные формулы легко записать в матричной форме:

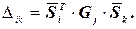(2.2)

В формуле (2.2) обозначены:

. (2.3)

для прямолинейных участков эпюр и и

. (2.4)

для криволинейной эпюры , которая аппроксимируется квадратной пара­болой.

В тех случаях, когда эпюра внутренних усилий имеет более сложный вид, например вид ломаной линии, состоящей из прямолинейных или криволиней­ных отрезков, выделяем отдельные отрезки эпюр, закон изменения уси­лия на которых одинаков. Всё это приводит к необходимости назначать отдельные участки на эпюрах. Назначают границы участков в начале и на конце эпюры, в точках появления или исчезновения нагрузок, в точках из­менения закона жесткости и в точках перелома оси стержня. На границах участков в столбец выписывают значения внутренних усилий для прямо­линейных участков. На криволинейных участках между граничными значе­ниями выписывают значение в середине участка. Если значения на обоих эпюрах усилий, на двух соседних, примыкающих друг к другу участках одинаковы, то они записываются один раз. При этом значения в матрице податливости G, суммируются и записываются на главной диагонали мат­рицы с тем же номером, что и номер усилия на эпюрах.

Пример №10: Дано:

Рама загружена, направленной вниз, равномерно распределенной нагруз­кой q=1 кН/м, сосредоточенной силой F=6 кН и парой сил с моментом m=6 кНм.

Найти вертикальное перемещение точки А, горизонтальные перемещения точек А, B, C и D, угол поворота сечения С.

Решение:

Строим эпюру изгибающих моментов M_F от действия заданной нагрузки (Рис.2.4.). Для определения перемещений задаем вспомогательные единичные на­гружения F₁=1, F₂=1, F₃=1 и m=1 и строим единичные эпюры изгибающих моментов (Рис.2.5):

.

Составляем исходные матрицы. С этой целью разбиваем раму на участки: 1-й участок – консоль ригеля рамы, 2-й участок – ригель рамы между стойками, 3-й участок – левая стойка, 4-й участок – правая стойка рамы.

Рис.2.5. Единичные эпюры изгибающих моментов (к примеру №10)

Так как на консоли эпюра моментов криволинейна, берем ординаты в трех токах, кроме ординат на концах пишем ординату в середине участка. На остальных участках выписываем только ординаты на концах участков.

Составляем исходные матрицы:

Перемножим матрицы:

вертикальное перемещение точки А, и горизонтальные перемещения точек A, B, и С:

горизонтальное перемещение точки D:

угол поворота сечения C:

Пример №11: Дано:

Найти:

углы поворотов сечений А и Е и вертикальные перемещения сечений С и E.

Решение:

(см. Рис.2.6)

Строим эпюру изгибающих моментов от заданной нагрузки Эп.M_F.

Выбираем вспомогательные состояния балки, загрузив ее единичными моментами m_A=1, m_E=1 для определения углов поворотов, и единичными силами F_C=1 и F_E=1. Строим эпюры изгибающих моментов Эп.M_AM, Эп.M_CF, Эп.M_EF и Эп.M_EM.

Формируем матрицы изгибающих моментов и и матрицу подат­ливости G. Разбиваем балку на участки I. II, III, IV. На участке I, где эпюра изгибающих моментов криволинейна, введем дополнительное сече­ние посредине. На границах участков изгибающие моменты в конце пре­дыдущего равны моментам в начале следующего на всех эпюрах, поэтому в матрицах и записываем их один раз. Введем основную длину l₀ и основную жесткость EI₀. Вычислим коэффициенты: примем l₀ =2 м, EI₀=EI:

Формируем матрицы

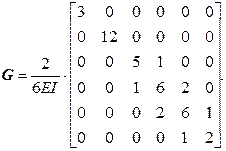
Перемножим матрицы:

Ответ:

Date: 2015-12-10; view: 1047; Нарушение авторских прав