Силы в механике

Все многообразие встречающихся в природе взаимодействий сводится всего лишь к четырем типам. Это гравитационное электромагнитное, ядерное (или сильное) и слабое взаимодействие. В механике Ньютона можно рассматривать только гравитационное и электромагнитное взаимодействия. В отличие от короткодействующих ядерного и слабого взаимодействия, гравитационное и электромагнитное взаимодействия – дальнодействующие: их действия проявляются на очень больших расстояниях.

Название силы	Природа взаимодействия	Формула для расчета силы	Зависимость силы от расстояния или относительной скорости	Зависит ли сила от массы взаимодействующих тел	Как направлена сила
Сила тяготения	гравитационная		Является функцией расстояния между взаимодействующими телами	Прямо пропорциональна массам взаимодействующих тел	Вдоль прямой, соединяющей взаимодействующие тела
Сила упругости	электромагнитная		Является функцией расстояния (зависит от деформации)	Не зависит	Противоположно направлению перемещения частиц при деформации
Сила трения а)сухого б)жидкого	электромагнитная		Является функцией скорости относительного движения	Не зависит	Противоположно направлению вектора скорости

СИЛЫ В МЕХАНИКЕ
Основные формулы
• Закон всемирного тяготения

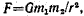
где F — сила взаимного притяжения двух материальных точек; m1 и m2 — их массы; r — расстояние между точками; G — гравита­ционная постоянная.

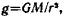
В написанной форме закон всемирного тяготения можно приме­нять и к взаимодействию шаров, масса которых распределена сфери­чески-симметрично. В этом случае r есть расстояние между центра­ми масс шаров.
• Напряженность гравитационного поля

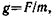
где F — сила тяготения, действующая на материальную точку массы m, помещенную в некоторую точку поля.
• Напряженность гравитационного поля, создаваемого плане­той, массу М которой можно считать распределенной сферически-симметрично,

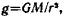
где r — расстояние от центра планеты до интересующей нас точки поля, находящейся вне планеты.
• Ускорение свободного падения на высоте h над поверхно­стью Земли

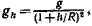
где R — радиус Земли; g — ускорение свободного падения на по­верхности

Земли. Если

, то

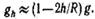
• Потенциальная энергия гравитационного взаимодействия двух материальных точек массами m1 и m2 (шаров с массой, распре­деленной сферически симм етрично), находящихся на расстоянии r друг от друга

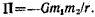
(Потенциальная энергия бесконечно удаленных друг от друга ма­териальных точек

принята равной нулю.)
• Потенциал гравитационного поля

где П — потенциальная энергия материальной точки массой m, помещенной в данную точку поля.
• Потенциал гравитационного поля, создаваемого планетой, массу М которой можно считать распределенной сферически-сим­метрично,

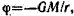
где r — расстояние от центра планеты до интересующей нас точки поля, находящейся вне планеты.
• Законы Кеплера.
1. Планеты движутся по эллипсам, в одном из фокусов которых находится Солнце.
2. Радиус-вектор планеты в равные времена описывает одинако­вые площади.
3. Квадраты периодов обращения любых двух планет относятся как кубы больших полуосей их орбит:

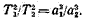
Законы Кеплера справедливы также для движения спутников вокруг планеты.
• Относительная деформация при продольном растяжении или сжатии тела

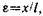
где? — относительное удлинение (сжатие); x — абсолютное удли­нение (рис. 4.1); l — начальная длина тела.

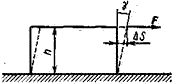
Относительная деформация при сдвиге определяется из формулы

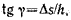
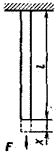
Рис. 4.1 Рис. 4.2

Date: 2015-11-15; view: 290; Нарушение авторских прав