Пример 1. Пусть в ящик вложено 16 предметов разной фирмы и цвета

Пусть в ящик вложено 16 предметов разной фирмы и цвета. Спрашивается: сколько двоичных единиц информации будет содержаться в сообщении, когда мы выбираем только один из 16 предметов, например, красный кубик? Метод вычисления прост. Вначале разобьем 16 предметов на две подгруппы по 8 предметов в каждой. В таком бинарном делении уже содержится одна двоичная единица информации, так как необходимо знать, в какой из групп находится красный кубик. Возьмем нужную подгруппу и снова разделим ее на две части, содержащие по 4 предмета, выбрав ту из них, в которой находится предмет сообщения. В этот момент мы затратили вторую двоичную единицу информации. И, наконец, выбрав из последней подгруппы красный кубик, мы дополним информацию четвертой двоичной единицей.

Таким образом, при сообщении о красном кубике, находившемся в группе из 16 предметов, мы должны были сделать 4 выбора, каждый из которых соответствовал одной двоичной единице информации.

Следовательно, в нашем сообщении об этом кубике содержались четыре двоичные единицы. Количество предметов в группе и подгруппах в процессе двоичного деления информации было следующим:

16; .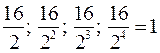

Отсюда видно, что степень числа 2 в последнем, четвертом, выборе является мерой информации в двоичных единицах исоответствует числу выборов.

Переходя от единичного примера к обобщенной формулировке и обозначая через n число предметов выбора, через Н – число выборов (т.е. количество двоичных единиц), можно записать: п = 2*.Отсюда следует:

Н = log ₂ n.

Иначе говоря, величина информации Н может быть определена как логарифм с основанием 2 от числа возможных выборов. Двоичный логарифм наиболее удобен, так как при этом в конечном выборе мы доходим до последней единицы отбора.

Разобранный пример относится к случаю отбора из равновероятных независимых событий. Указанную выше формулу можно распространить и на явления, встречающиеся с разной вероятностью.

В общем случае вышеизложенное можно представить следующим образом. Величина информации о любом из равновероятных событий определяется по формуле

,

где Н – информация о событии;

– вероятность события.

В том случае, если события (альтернативы) имеют разную вероятность, информация о каждом из них (индивидуальная информация) может быть найдена по аналогичной формуле:

,

где h_i – информация об i -ом событии;

p_{i –} вероятность i -го события.

Однако для решения многих задач знания об индивидуальной информации недостаточно. В этом случае пользуются формулой Шеннона:

,

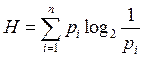где Н – среднее количество информации;

р_i – вероятность i -го события.

При этом следует заметить, что при равной вероятности событий h (индивидуальная информация) и H (средняя информация) совпадают.

Date: 2015-10-21; view: 311; Нарушение авторских прав