Свойства сложения векторов и умножения вектора на число

(a,b,c -векторы одинаковой размерности)

1) Коммутативность сложения векторов .

2) Ассоциативность сложения векторов .

3) Дистрибутивность сложения векторов .

4) Существование нулевого вектора ,

где -нулевой вектор (вектор, все компоненты которого равны нулю).

5) Существование противоположного вектора ,

где 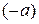- противоположный вектор, -нулевой вектор.

6) Ассоциативность умножения вектора на число ,

где 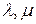- числа.

7) Дистрибутивность умножения вектора на число .

8) Существование единичного вектора .

Векторы широко используются во всех областях науки, в том числе и в экономической. Многие обозначения при использовании векторов очень компактны, при этом не теряют в наглядности и содержательности.

Пример 4.1. Пусть завод производит мужские, женские и детские велосипеды. Тогда объем его производства V за год можно записать как вектор (М, L, D), где М — объем производства за год мужских велосипедов, L — женских и D — детских. Например, пусть объем производства в 2003 г. был V = (1000, 800, 4000). Предположим, что план на 2004 г. на 10% больше объема производства в 2003 г., тогда этот план есть вектор V (1100, S80. 4400). Пусть торговая фирма «Велосипеды» покупает половину всей про­дукции завода, тогда в 2003 г. она купила W= (500, 400, 2000). Предполо­жим, что в стране всего три велосипедных завода, объемы производства, ко­торых в 2003 г. были Q =(1000, 800,4000), Q =(1000,600,2000), Q =(2000, 1600, 8000). Тогда все три завода вместе произвели Q =(4000, 3000, 14000), т.е. 4000 мужских, 3000 женских и 14 000 детских велосипедов. Можно также отметить, что Q =2 Q т.е. 3-й завод произвел в 2 раза больше велоси­педов каждого вида, чем 1-й завод.

Приведенные выше векторы V , V , W, Q , Q , Q и т.д. — это примеры конкретных векторов.

Определение. Совокупность всех n-мерных векторов с действительными компонентами, рассматриваемая с определенными над ней операциями сложения и умножения вектора на число, обладающими свойствами 1-8, называется n-мерным арифметическим векторным пространством и обозначается .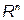

Примеры векторных пространств.

1) Пространство R² и R³.

Величины называются векторными или векторами, если каждая из них определяется численным значением и направлением, например сила, скорость, ускорение. Для векторов, как геометрических объектов (направленных отрезков), определяются геометрически операции сложения и умножения вектора на число. Сложение производится либо, используя правило параллелограмма, либо - веревочного многоугольника.

Произведением вектора на число 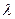называется вектор , определяемый следующими условиями

1) 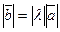, где 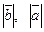- длины векторов;

2) ;

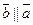3) вектора и одинаково направлены, если , и противоположно направлены если .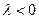

Операции сложения векторов и умножения вектора на число обладают свойствами (1-8) векторных пространств. Следовательно, совокупность векторов на плоскости и в пространстве образует векторные пространства R² и R³ соответственно.

2) Совокупность матриц размера образует векторное пространство, так как операции сложения матриц и умножения матрицы на число удовлетворяют свойствам (1-8) векторных пространств.

3) Совокупность многочленов степени не выше n является линейным пространством.

Замечание. Совокупность многочленов степени ровно n не является линейным пространством.

4) Множество функций, непрерывных на данном участке является линейным пространством.

5) Пространство товаров, вектор цен. Под товаром понимаются некоторое благо или услуга, поступившая в продажу в определенное время и в определенном месте. Будем считать, что имеется п различных товаров, количество i -го товара обозначается , тогда некоторый набор товаров обозначается Х= (), т.е. является n -мерным вектором. Будем рассматривать, как правило, только неотрицательные количества товаров, так что для любого i = 1,... п или X 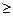0. Множество всех наборов товаров называется пространством товаров С. Это множество называется пространством, потому что в нем можно сложить любые два набора и умножить любой набор товаров на любое неотрицательное число. Возможность умножения набора товаров на любое неотрицательное число отражает предположение о безграничной делимости и умножении товаров (т.е. товары устроены наподобие сахарного песка, а не авианосцев).

В дальнейшем предполагаем, что каждый товар имеет цену. Все цены предполагаются строго положительными. Пусть цена единицы i -го товара есть , тогда вектор Р =() есть вектор цен.

Набор товаров, как вектор, имеет ту же размерность, что и вектор цен. Для набора товаров Х=() и вектора цен Р=( ) их скалярное произведение Р Х= есть число, называемое ценой набора или его стоимостью, и будет обозначаться с(Х).

Date: 2015-10-19; view: 607; Нарушение авторских прав