Дифференциальные уравнения установившегося движения упругой жидкости

Дифференциальное уравнение неразрывности потока выведено в параграфе 1.4. Если происходит установившееся фильтрация, то в этом уравнении производная по времени будет равна нулю. При фильтрации сжимаемой жидкости или газа плотность зависит от давления и поэтому ее нельзя вынести из под знака дифференциала:

.

(3.1)

Введем понятие массовой скорости, которая является произведением линейной скорости на плотность:

.

(3.2)

После такой замены дифференциальное уравнение неразрывности при установившемся движении примет такой же вид, что и для несжимаемой жидкости, только вместо линейной скорости будет стоять массовая скорость.

Используя закон Дарси, найдем массовую скорость:

.

(3.3)

Плотность сжимаемой жидкости или газа зависит от давления, поэтому введем вспомогательную функцию P, которую назовем функцией Лейбензона и определим ее как:

.

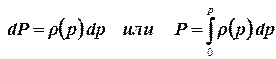(3.4)

Подставим массовую скорость, найденную из закона Дарси в уравнение неразрывности получим уравнение фильтрации сжимаемой жидкости или газа при установившемся движении. Оно также является уравнением Лапласа, только вместо давления в него входит функция Лейбензона.

.

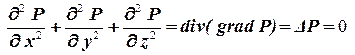(3.5)

Аналогия с движением несжимаемой жидкости

С введением функции Лейбензона сравним уравнения, полученные в предыдущем параграфе, с уравнениями фильтрации несжимаемой жидкости.

Несжимаемая жидкость	Сжимаемая жидкость или газ
r = const(p)	r = r(p) ¹ const(p)
Уравнение неразрывности потока
	um = r u
Q = u w = const(p)	Qm = um w = rат Qат = const(p)
Закон Дарси
Аналогия между величинами
Линейная скорость - u	um – Массовая скорость
Объемный расход - Q	Qm = rат Qат – массовый расход
Давление - p	P- функция Лейбензона

Сравнение уравнений позволяет установить аналогию между установившейся фильтрацией сжимаемой жидкости или газа и установившейся фильтрацией несжимаемой жидкости, для которой законы фильтрации были детально разобраны в главе 2. Отсюда следует вывод, что все формулы, полученные для установившейся фильтрации несжимаемой жидкости по закону Дарси, можно использовать и для установившейся фильтрации сжимаемого флюида в пластах той же геометрии и при тех же граничных условиях. Для этого необходимо в формулах несжимаемой жидкости заменить:

линейную скорость – u Þ u_m – массовую скорость;

объемный расход – Q Þ Q_m – массовый расход;

давление – p Þ P - функцию Лейбензона.

Подчеркнем, что при фильтрации газа плотность зависит от абсолютного давления, то давление p в этом случае - абсолютное давление.

Рассмотрим вид функции Лейбензона для некоторых частных случаев.

Несжимаемая жидкость. Для несжимаемой жидкости плотность не зависит от давления (r = r_o = const(p)), поэтому ее можно вынести из под знака интеграла и функция Лейбензона примет вид:

.

(3.6)

Идеальный газ. Для идеального газа плотность зависит от давления

,

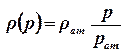(3.7)

поэтому функция Лейбензона после интегрирования примет вид:

.

(3.8)

Реальный газ. Для реального газа плотность зависит от давления

.

(3.9)

Коэффициент сверхсжимаемости реального газа z(p) достаточно сложным образом зависит от давления, поэтому интеграл вычислить затруднительно. В этом случае z(p) заменяют средним значением на промежутке изменения давления в пласте z_ср и функция Лейбензона после интегрирования примет вид:

.

(3.10)

Приток газа к галерее по закону Дарси

Исследуем установившийся плоскопараллельный фильтрационный поток идеального газа. Для этого воспользуемся аналогией между фильтрацией несжимаемой жидкости и газа. Запишем формулу дебита притока к галерее для несжимаемой жидкости:

.

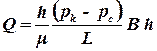(3.11)

Прозведем в этом уравнении замены. Заменим давление p на функцию Лейбензона P, а объемный расход Q на массовый расход Q_m.

.

(3.12)

В последней формуле распишем функцию Лейбензона, тогда массовый расход галереи будет рассчитываться по формуле:

(3.13)

А приведенный к атмосферным условиям объемный расход

,

(3.14)

Расчет распределения давления по галерее производится в той же последовательности:

(3.15)

Скорости фильтрации в любой точки вокруг скважины можно найти из урвнения неразрывности:

(3.16)

Рис. 3.1 . а) изменение давления по длине галереи; б) изменение отношение скорости фильтрации в пласте к скорости фильтрации на галереи.

На рис. 3.1 приведены распределение давления по галереи при фильтрации газа и нефти. Для нефти линия распределения давления прямая линия, а для газа – парабола. При фильтрации газа градиенты давления при малых давлениях больше, чем при больших, поэтому и скорости фильтрации при малых давлениях больше, чем при больших.

Date: 2015-10-19; view: 1639; Нарушение авторских прав