Плоскорадиальный поток идеального газа при нарушении закона Дарси

Вблизи большинства газовых скважин происходит нарушение закона Дарси, поэтому расчеты, связанные с разработкой газовые месторождений, а также с исследованием скважин, проводят обычно по нелинейным законам фильтрации. При этом нельзя использовать для расчета дебита скважины формулу Дюпюи и нельзя использовать аналогию между фильтрацией жидкости и газа, так как они выведены с учетом движения по закону Дарси.

Пусть в газовом пласте толщиной h и проницаемостью k пробурена скважина радиусом r_c. На скважине поддерживается давление p_c, а на контуре питания радиусом R_k давление p_k. В пласте происходит фильтрация газа по нелинейному (двухчленному) закону фильтрации. Необходимо рассчитать дебит скважины и распределение давления вокруг скважины. Математически эта задача описывается уравнением неразрывности потока

(3.27)

Нелинейным законом фильтрации:

(3.28)

Зависимостью плотностью газа от давления

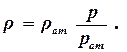
(3.29)

И граничными условиями:

(3.30)

Эту систему уравнений будем решать методом исключения переменных. Из уравнения неразрывности найдем скорость фильтрации и подставим в нелинейный закон фильтрации. При этом исключается скорость фильтрации из уравнения фильтрации:

.

(3.31)

Выразим массовый расход через объемный расход при атмосферном давлении, а плотность через давление

.

(3.32)

Полеченное дифференциальное уравнение первого порядка будем интегрировать методом разделения переменных. Для этого умножим уравнение на 2 p dr:

.

(3.33)

Для того, чтобы найти распределение давления вокруг скважины будем интегрировать это уравнение по давлению от давления на скважине p_c до текущего давления p(r), а по радиусу от радиуса скважины r_c до текущего радиуса:

(3.34)

Для нахождения дебита скважины воспользуемся вторым граничным условием – заданным давлением p_k на контуре питания. Пренебрегая 1/R_k во втором слагаемом (1/R_k<<1/r_c) получим:

.

(3.35)

Обычно вводят обозначения

.

(3.36)

Тогда уравнение расчета дебита примет вид

.

(3.37)

Коэффициенты “ a ” и “ b ” называются коэффициентами фильтрационных сопротивлений и определяются опытным путем по данным исследования скважины при установившихся режимах. Для нахождения дебита скважины по известным значениям “ a ”, “ b ” и разницы квадратов давлений необходимо решить квадратное уравнение:

.

(3.38)

В этом уравнении выбираем знак + так, как дебит скважины не может быть отрицательным. При b ® 0 последнее уравнение приводит к неопределенности типа 0/0, поэтому преобразуем это уравнение к виду, в котором этой неопределенности нет:

.

(3.39)

Date: 2015-10-19; view: 565; Нарушение авторских прав