Пример 11. Метод графов в выборе оптимального набора средств рекламы

Метод графов в выборе оптимального набора средств рекламы.

Пусть имеется N средств рекламы. Обозначим –а - переменные затраты на разработку и изготовление j-го средства рекламы; b -постоянные затраты, p - маржинальная прибыль рекламного агентства с единицы j-го средства рекламы, v - потребность в j-ом средстве рекламы для охвата ЦА.

Пусть стандартный пакет РК состоит из N средств рекламы. Совокупная маржинальная прибыль РА составит P(N)= , постоянные издержки B(N)= , прибыль (П) РА от создания набора N средств рекламы составит П(N)=P(N)-B(N) Для определения оптимального набора средств рекламы, обозначим через m –число различимых, желаемых потребителем, доминирующих атрибутов в рекламируемом товаре, -множество средств рекламы,которые могут реализовать j-ый атрибут, v 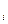-количество j-ых средств рекламы, реализующих i-ый атрибут товара с целью удовлетворения желаний ЦА. Пусть из N средств рекламы -множество атрибутов товара, реализуемых j-ым средством рекламы. Потребность в j-ом средстве составит v = 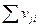, i=1,…,w

В качестве допущений примем, что инфляция на период РК отсутствует, скидки за объем произведенной рекламы отсутствуют.

Множество средств рекламы N будем называть достаточным, если для любого доминирующего атрибута товара найдется такое j средство рекламы, что i w Т.е. достаточный (стандартный) набор должен быть и полным множеством средств рекламы. Определим полное множество N, для которого величина прибыли РА была бы максимальна:

П(N)=

Рассмотрим решение задачи по моделям теории графов. Для этого построим двудольный граф \G(X,Y,V), где X-множество вершин, соответствующих средствам рекламы; Y- множество вершин, соответствующих доминирующим атрибутам(потребностям потребителей рекламы товара).Вершины j соединяются дугами с вершинами j только в том случае, когда i w , т.е рекламное средство j реализует доминирующий атрибут I в сознании потребителей рекламы. Для каждой вершины j зададим числа b ,p . А для дуги- v

Обозначим n -множество средств рекламы из N (n , каждый из которых может реализовать атрибут i.Целевая функция выбора оптимального средства рекламы для реализации i-го атрибута с получением максимальной прибыли запишется так:

П(n

В этом случае решение задачи сводится к поиску покрытия двудольного графа,для которого целевая функция принимает максимальное значение.

Рассмотрим пример. Имеется 4 вида средств рекламы и 4 доминирующих атрибута товара или групп атрибутов или вообще сегментов потребителей рекламы из ЦА. Рекламное средство 1 может реализовать 1 доминирующий атрибут или удовлетворить потребности 1 сегмента, средства 2-1 и 2 сегмент, средство 3- 1.2 и 3 сегмент, средство 4 –все сегменты потребителей. Двудольный граф примет вид

Рис. 1.3. Двудольный граф

Числа p b , соответствующие маржинальной прибыли и постоянным издержкам для j-го средства рекламы указаны в квадратных скобках с размерностью тыс.руб.около каждой вершины 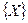, а значения v 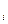, соответствующие величине i-го сегмента потребителей, в скобках у вершин В такой постановке существуют следующие варианты решения задачи:

1) достаточность набора рекламных средств обеспечивает N= , при этом первое рекламное средство удовлетворяет первый сегмент в объеме v 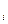=10 единиц, второе в v2=20, четвертое в v4=v3+v4=20Тогда П(1;2;3)=

2)набор средств рекламы включаетN= , тогда при v v 40 П (1;4)=

3)набор состоит из второго и четвертого рекламного средства N= ,когда второе средство удовлетворяет первый и второй сегмент с v 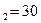, а четвертое –третью и четвертую с v Тогда П (2;4)=

4)набор включает только четвертое рекламное средство, которое удовлетворяет все потребности в объеме v , т.е. П(4)=100-20=80

Результаты вычислений по графу свидетельствуют, что оптимальным является третий вариант из набора 2 и 3 средств рекламы.

Существует ряд частных случаев в рассмотрении задачи проведения рекламных акций и распределения рекламного бюджета по акциям. Примем, что среди рекламных средств существует их упорядоченный ряд Ry= , в котором каждое предыдущее рекламное средство действеннее последующего за ним. Построим граф, в котором вершины соответствуют средствам рекламы j 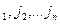и одна вершина j является выходом из РК, а вершина j 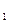является началом РК. Длина дуги в графе определится как

,v

Экономический смысл дуги графа между вершинами j и j состоит в получении прибыли от j рекламного средства. Средство j удовлетворяет все потребности за исключением тех. Которые может удовлетворить средство j .Тогда, любому набору рекламных средств соответствует некоторый путь на графе, соединяющий вход j 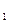с выходом j .Длина пути равна прибыли, получаемой от соответствующего этому пути стандартного набора средств рекламы. Таким образом, задача сводится к поиску критического пути на графе, имеющем максимальную длину. Преобразуем исходный граф в сеть на рис.1.4.

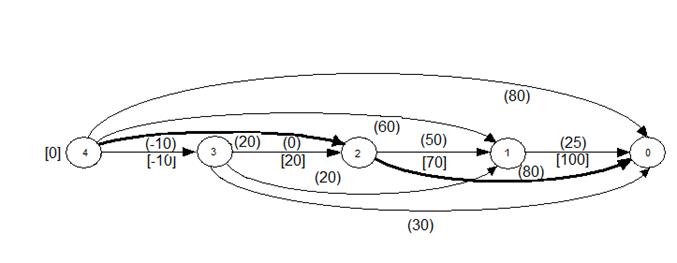
Рис.1.4. Преобразование графа

Расчетные длины дуг указаны в скобках. Для определения критического пути максимальной длины эффективнее использовать алгоритм ФОРДА. Потенциал вершины j 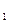полагается равным нулю, а потенциал следующих вершин из =max ,k 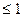Это есть метод динамического программирования, в котором, когда потенциал вершины j , это и есть искомый критический путь. Он определяется с максимальной вершины j в j , что соответствует и т.д.На рис.2 потенциалы вершин, описанные алгоритмом, указаны в квадратных скобках у соответствующих вершин. Критический путь выделен жирными дугами множества N=

Date: 2015-10-19; view: 511; Нарушение авторских прав