Задача 3.4

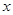
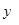
	Прогноз

Решение.

Итого 214

;

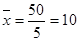n = 5

Линейный коэффициент корреляции:

Полученная величина линейного коэффициента корреляции свидетельствует о возможном наличии достаточно тесной прямой зависимости между рассматриваемыми признаками.

Коэффициент детерминации.

(r²) - коэффициент детерминации.

(r²)=(0,9726)²=0,9460

Для рассматриваемого примера коэффициент детерминации равен 0,9460, а это означает, что 94,60% вариации y объясняется вариацией x.

Теоретической линией регрессии называется та линия, вокруг которой группируются точки корреляционного поля и которая указывает основное направление, основную тенденцию связи. Эта линия должна быть проведена так, чтобы сумма отклонений точек поля корреляции от соответствующих точек теоретической линии регрессии равнялась нулю, а сумма квадратов этих отклонений была бы минимальной величиной.

Теоретически обосновать форму связи каждого из факторов с результативным показателем можно далеко не всегда, поскольку исследуемые социально-экономические явления очень сложны и факторы, формирующие их уровень, тесно переплетаются и взаимодействуют друг с другом.

Однако исходя из графического анализа имеющихся данных, а также основываясь на экономической специфике взаимосвязи рассматриваемых показателей, следует сделать вывод о целесообразности выбора линейной формы регрессионной зависимости.

Метод наименьших квадратов применяется для нахождения параметров уравнения регрессии. При применении метода наименьших квадратов для нахождения такой функции, которая наилучшим образом соответствует эмпирическим данным, считается, что сумма квадратов отклонений эмпирических точек теоретической линии регрессии должна быть величиной минимальной.

Критерий метода наименьших квадратов можно записать следующим образом:

В случае, когда уравнение регрессии представлено виде прямой линии

критерий метода наименьших квадратов имеет вид:

Функция двух переменных S(a,b) может достигнуть экстремума в том случае, когда первые частные производные этой функции равняются нулю, т.е. когда

Вычисляя эти производные, получим:

Отсюда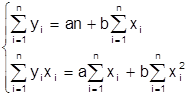

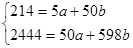
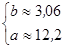
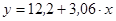
Корреляционное отношение:

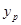
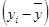
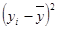
		24,44	1,56	2,4336	-16,8	282,24
		33,62	2,38	5,6644	-6,8	46,24
		42,8	-4,8	23,04	-4,8	23,04
		48,92	-2,92	8,5264	3,2	10,24
		64,22	3,78	14,2884	25,2	635,04
Итого 214				53,9528		996,8

Корреляционное отношение: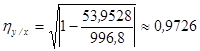

Правильность выбора линейной формы связи между показателями подтверждает близость коэффициента корреляции корреляционному отношению. Найдем разность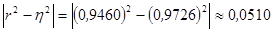

Проверка на существенность коэффициента корреляции производится с помощью критерия 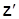Фишера.

Расчетный квантиль: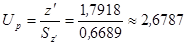

Следовательно, для уровня значимости

Оценка надежности модели производится с помощью показателя остаточной колеблемости и коэффициента вариации.

Показатель остаточной колеблемости:

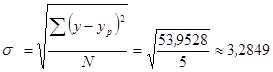
Коэффициент вариации: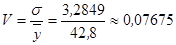

В соответствии с проведенным анализом можно сделать вывод о том, что линейная модель адекватна статистическим данным, а следовательно, можно рассчитать прогнозное значение при

Date: 2015-10-19; view: 290; Нарушение авторских прав